1. Der Vektorbegriff
← Kapitelübersicht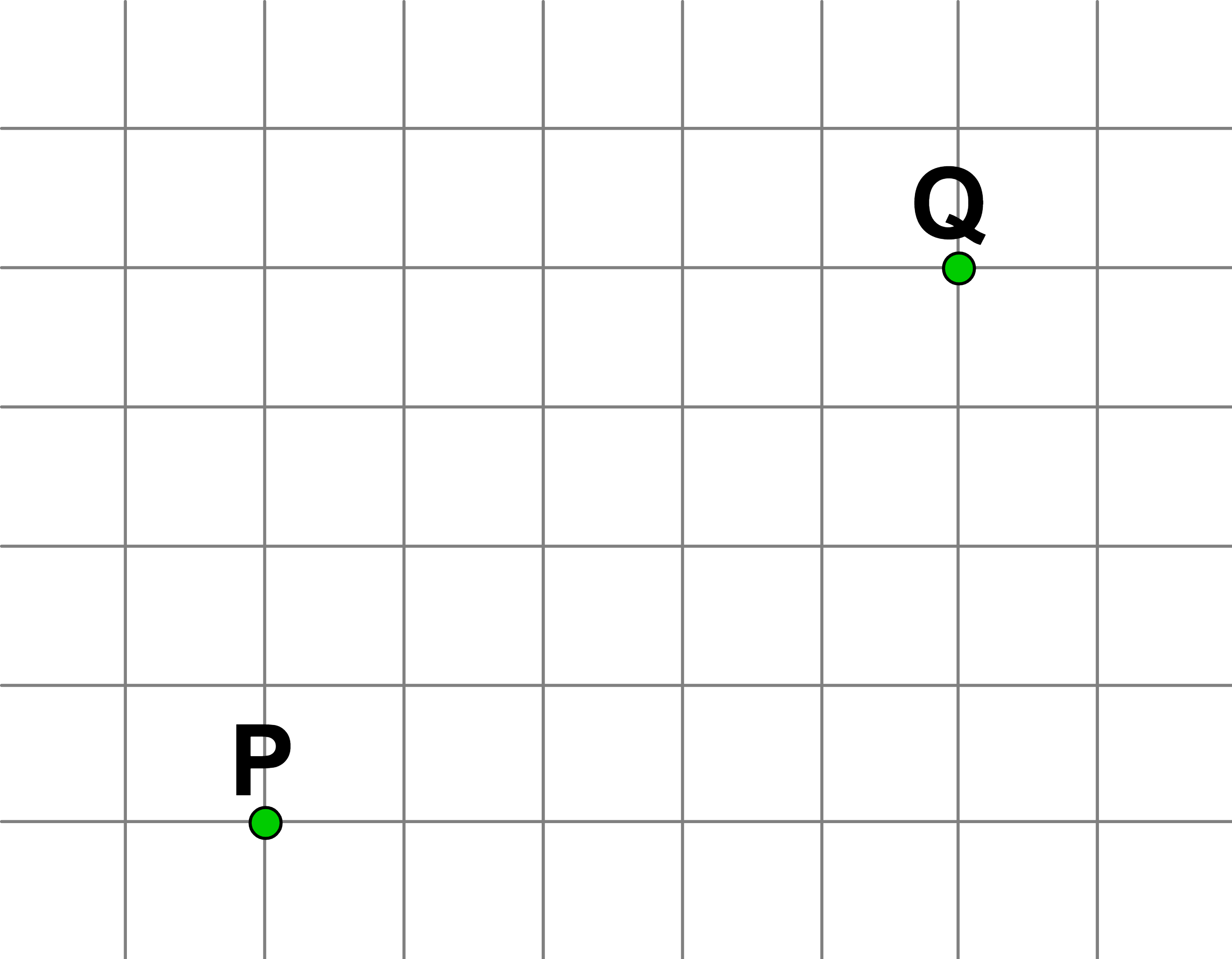
Die Punkte P und Q liegen in der Zeichenebene.
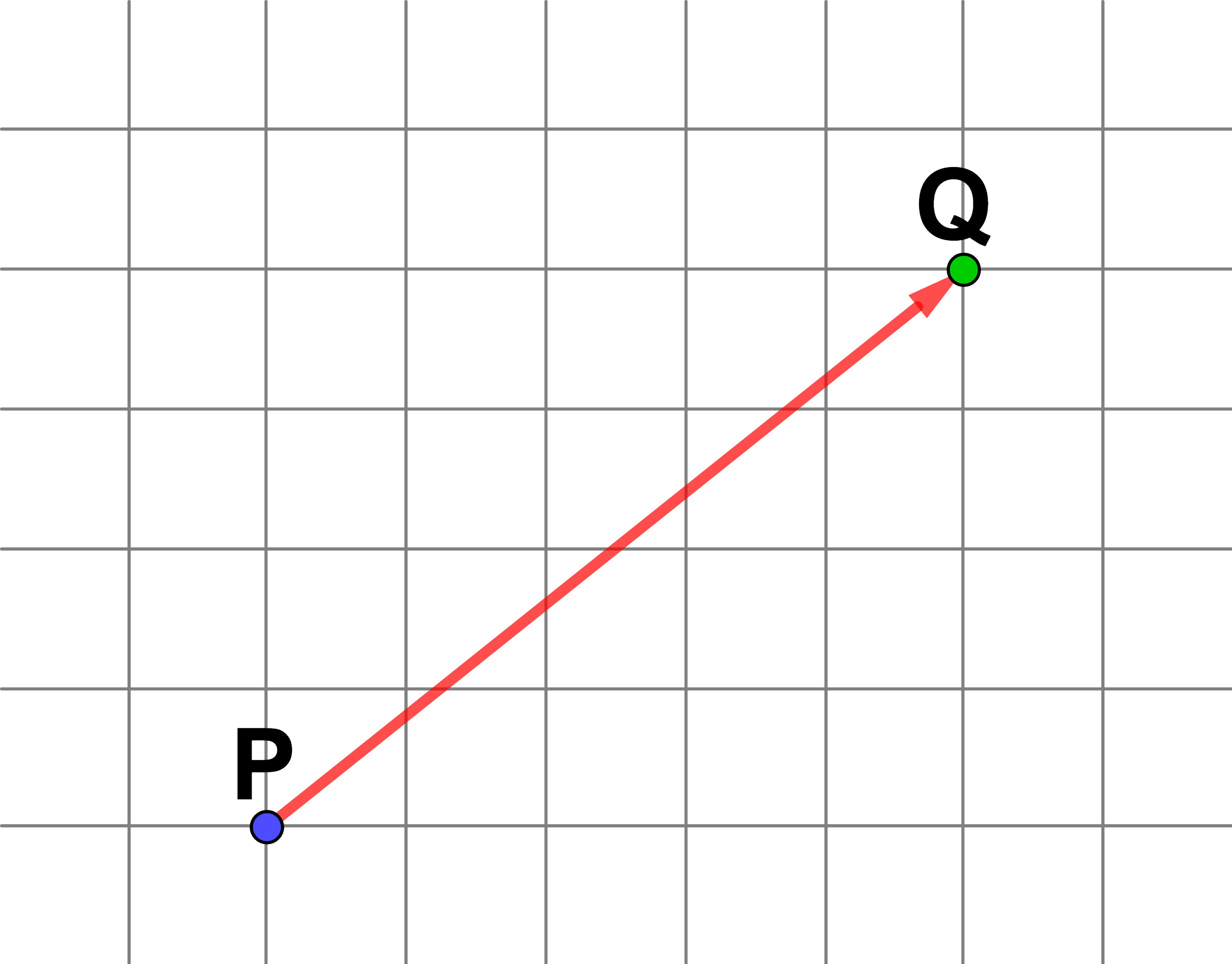
Der blaue Punkt, der auf P liegt, soll nach Q verschoben werden.
Der Weg, den ein Punkt bei seiner Verschiebung zurücklegt, wird durch einen Pfeil gekennzeichnet.
P heißt Anfangspunkt der Verschiebung.
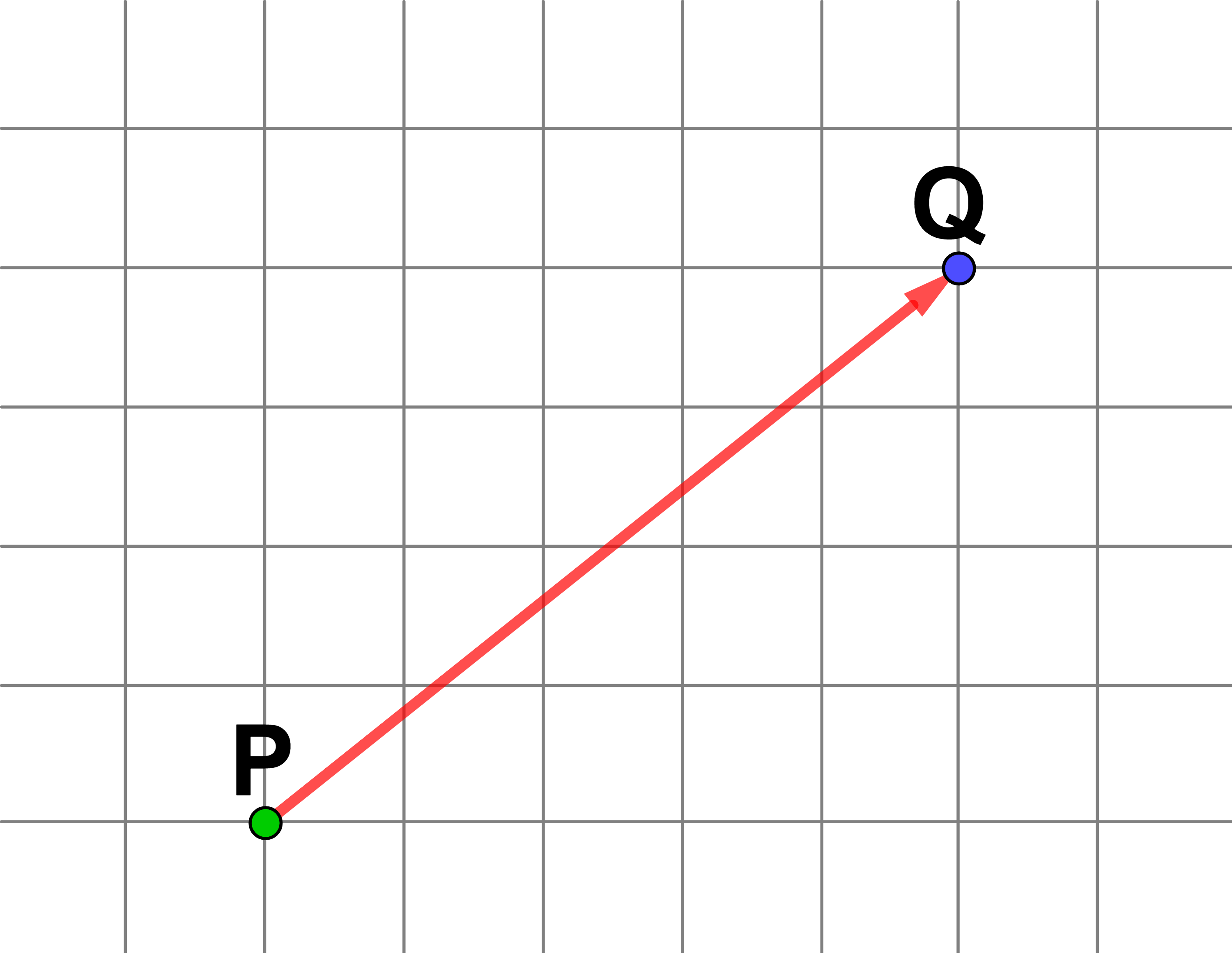
Der blaue Punkt ist von P nach Q verschoben worden.
Q heißt Endpunkt der Verschiebung.
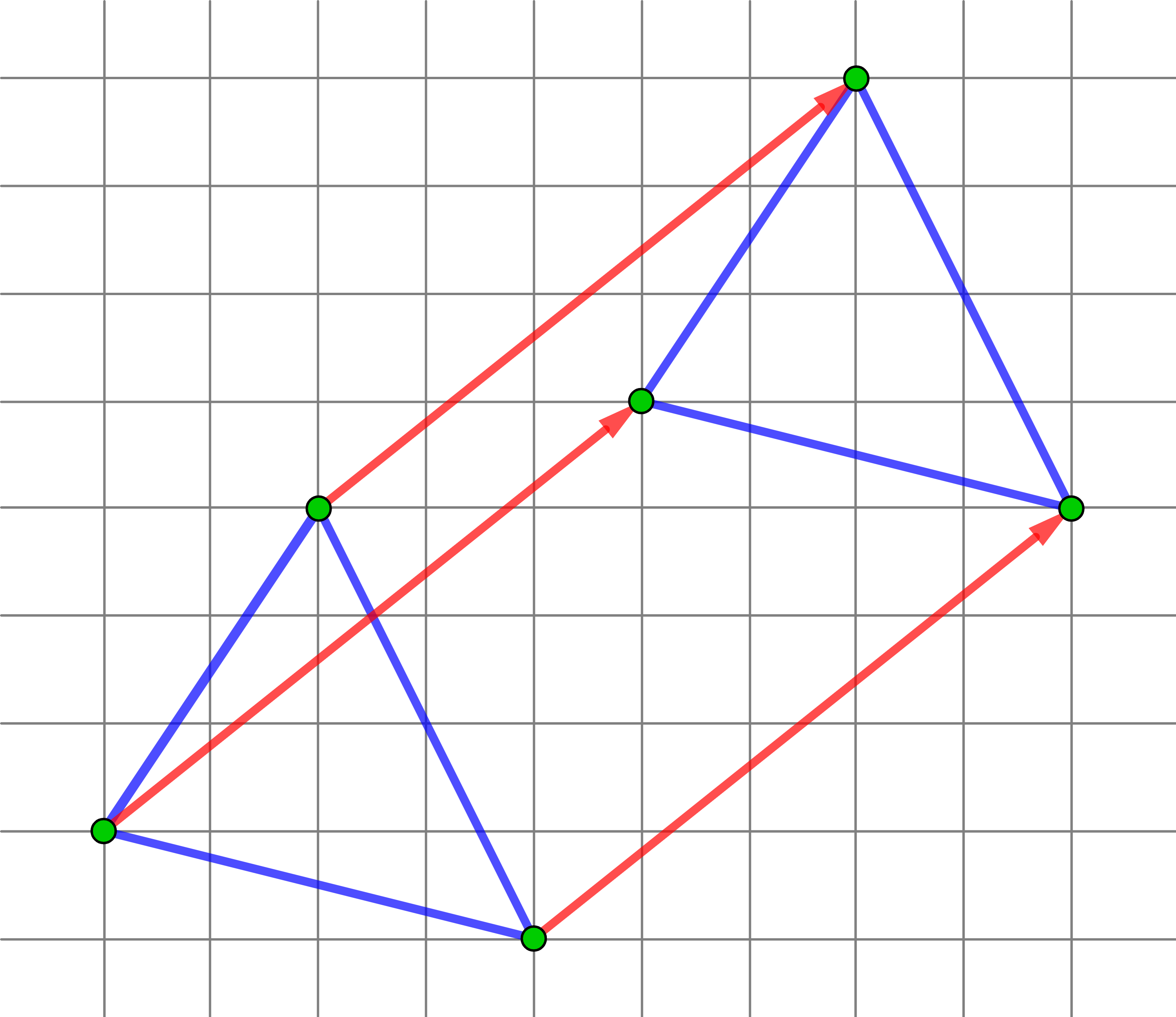
Wird eine Figur in der Ebene bzw. eine Figur oder ein Körper im Raum verschoben, sind alle Pfeile, die den Vektor (d.h. die Verschiebung) darstellen (man sagt: "repräsentieren"), gleich lang, parallel und sie haben die gleiche Orientierung, das heißt die Pfeilspitzen zeigen in dieselbe Richtung.
In der Zeichnung wird die Verschiebung des Dreiecks durch drei Pfeile, die von den Eckpunkten des Dreiecks ausgehen, repräsentiert.
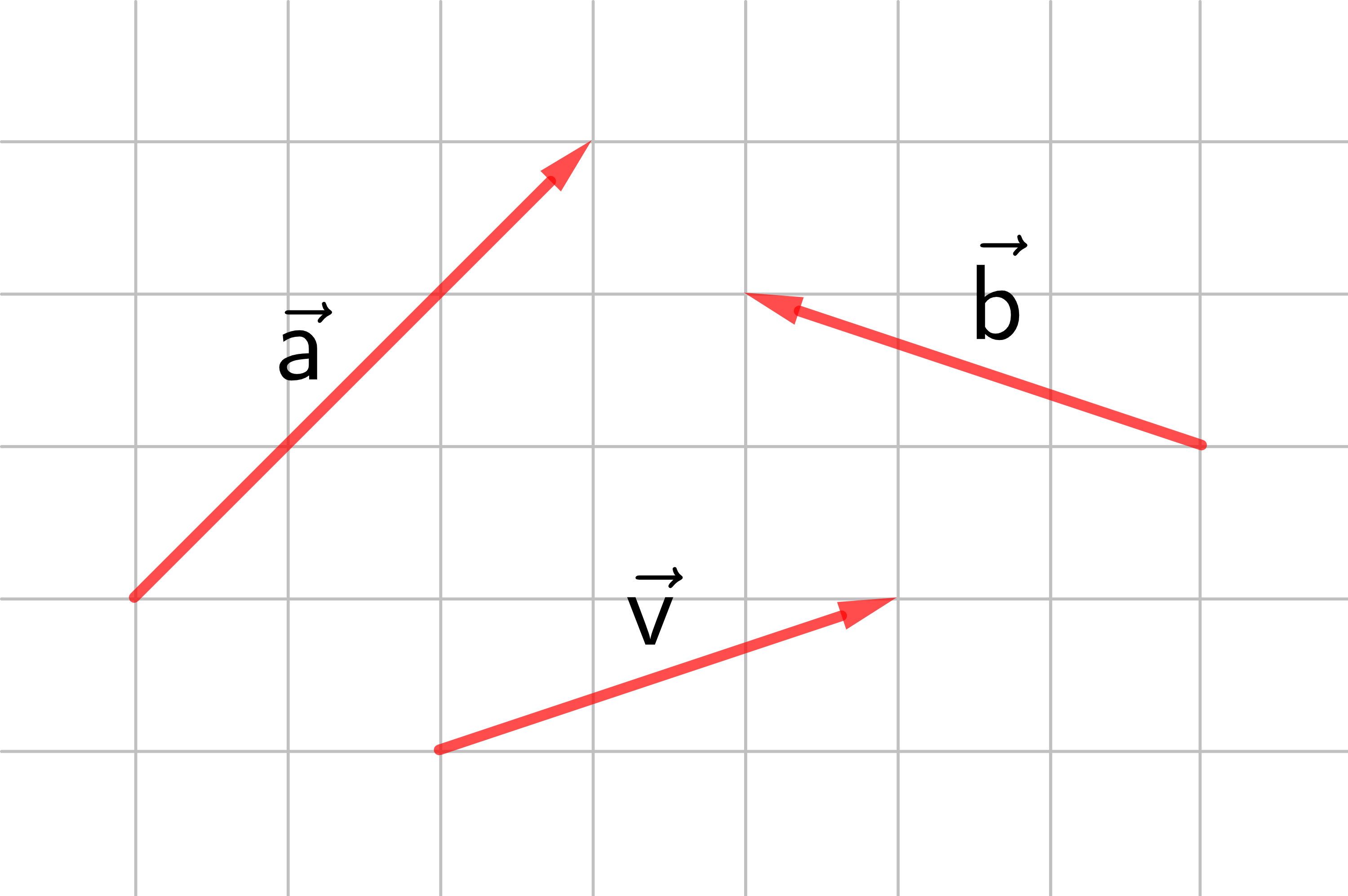
Um Vektoren (= Verschiebungen) voneinander unterscheiden zu können, muss man sie kennzeichnen. Das macht man üblicherweise durch kleine Buchstaben mit einem Pfeil darüber.
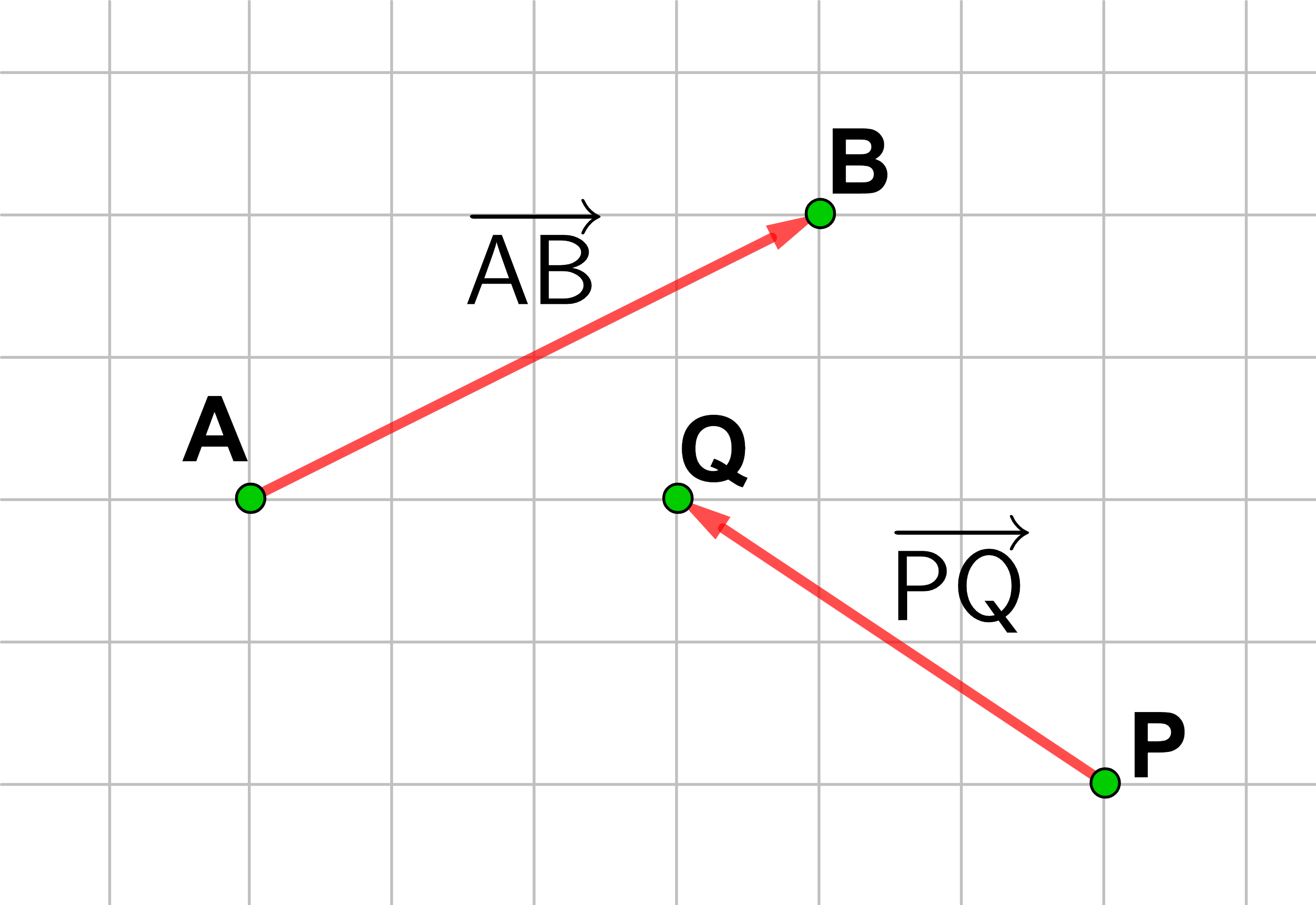
Kennt man einen Anfangspunkt und einen Endpunkt einer Verschiebung, kann man den Vektor mit Hilfe dieser Punkte benennen.
→
AB
ist der Vektor, der einen auf A liegenden Punkt nach B verschiebt.
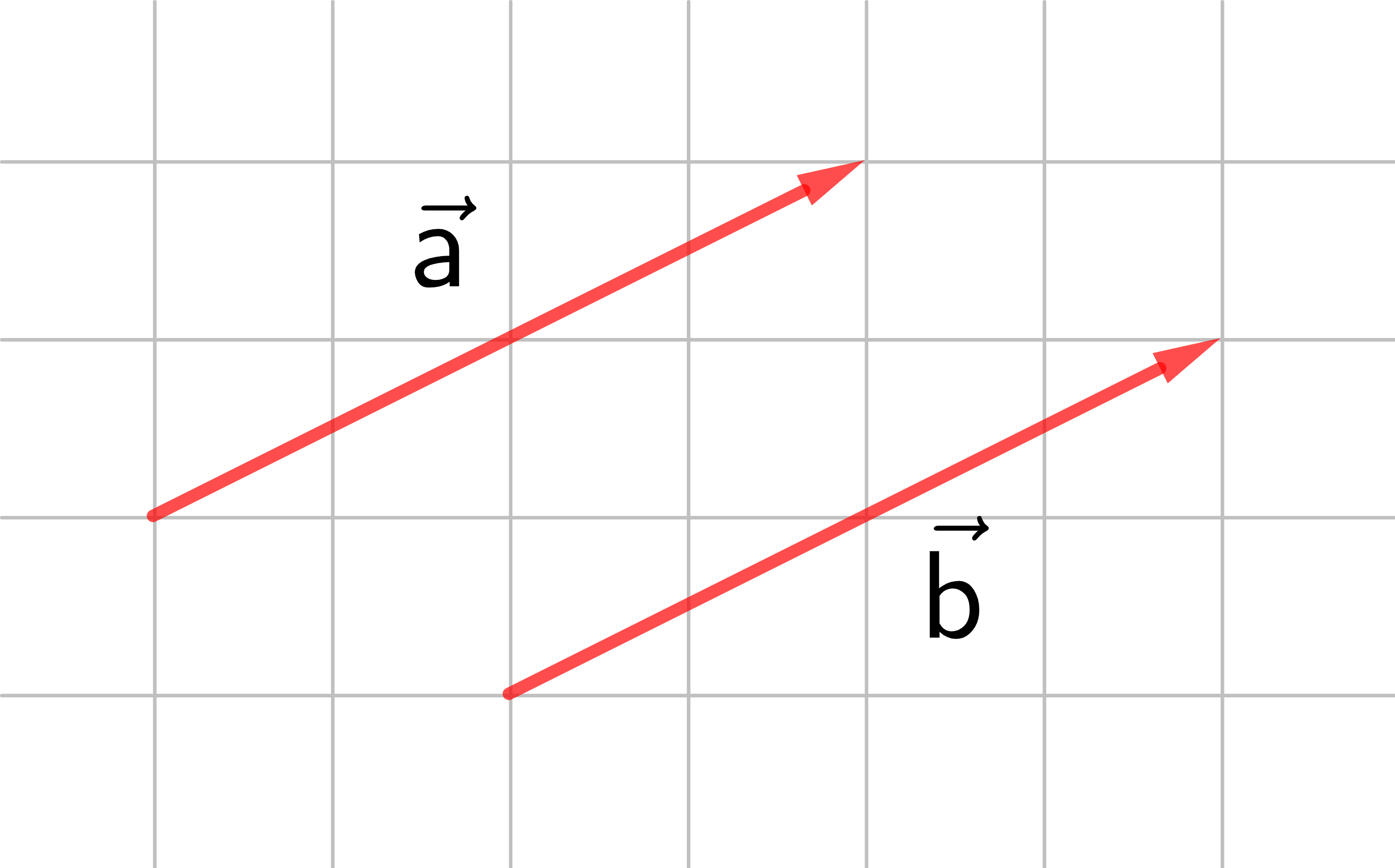
Sind die Pfeile, die zwei Vektoren repräsentieren, parallel und haben sie die gleiche Länge und Orientierung, dann gehören sie zur selben Verschiebung, auch wenn sie unterschiedliche Anfangspunkte haben.
In der Zeichnung sind die Vektoren
→
a
und
→
b
identisch:
→
a
=
→
b
.
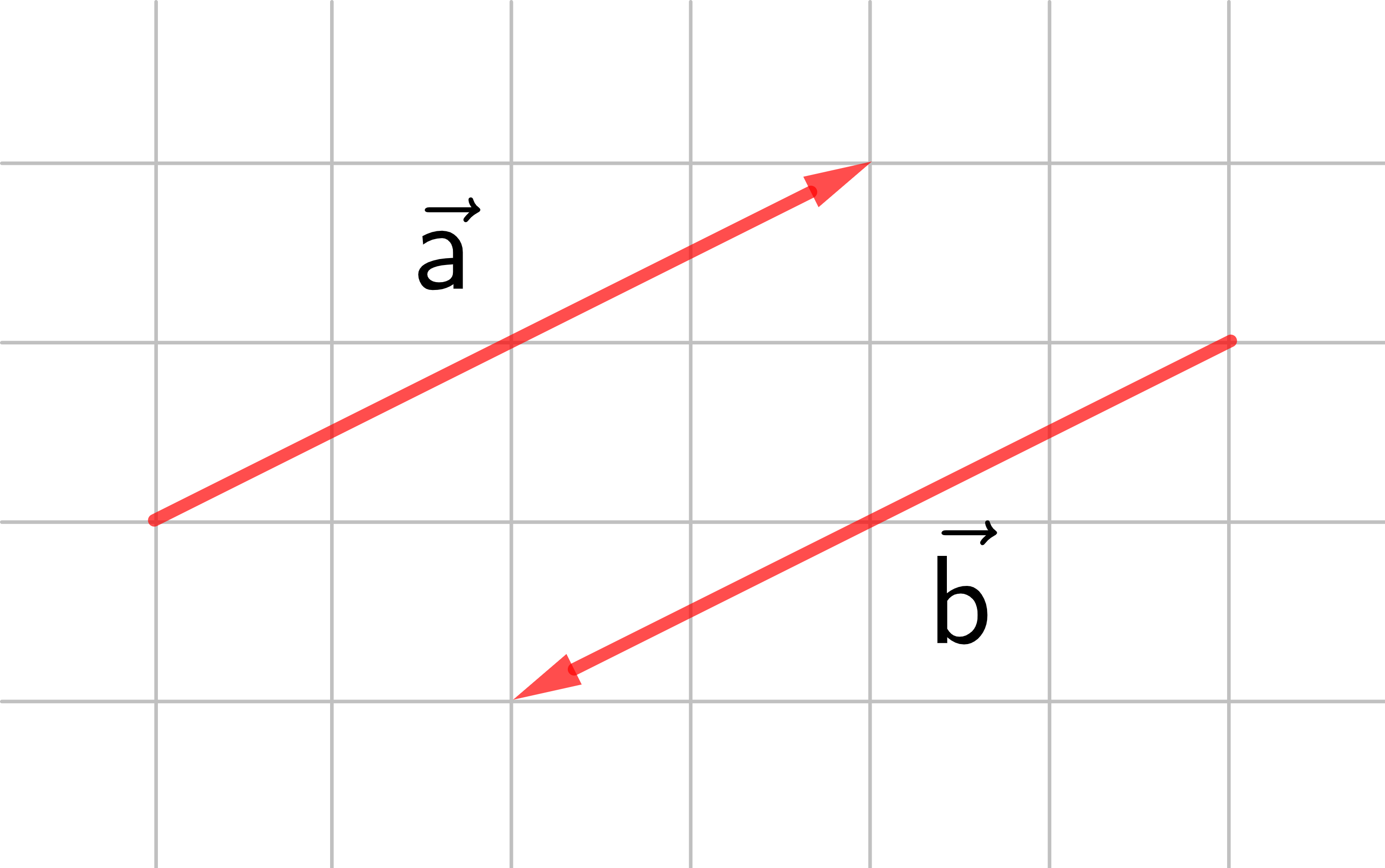
Vektoren, deren Pfeile parallel und gleich lang sind, aber entgegengesetzte Orientierung haben, heißen Gegenvektoren.
In der Zeichnung sind
→
a
und
→
b
Gegenvektoren.
Man schreibt:
→
a
=
−
→
b
oder
→
b
=
−
→
a
.
Übung:
In der nachfolgenden Zeichnung sind verschiedene Vektoren in der Ebene dargestellt. Entscheiden Sie, ob die im gelben Kasten angezeigte Gleichung wahr oder falsch ist. Klicken Sie auf die zutreffende Antwort.
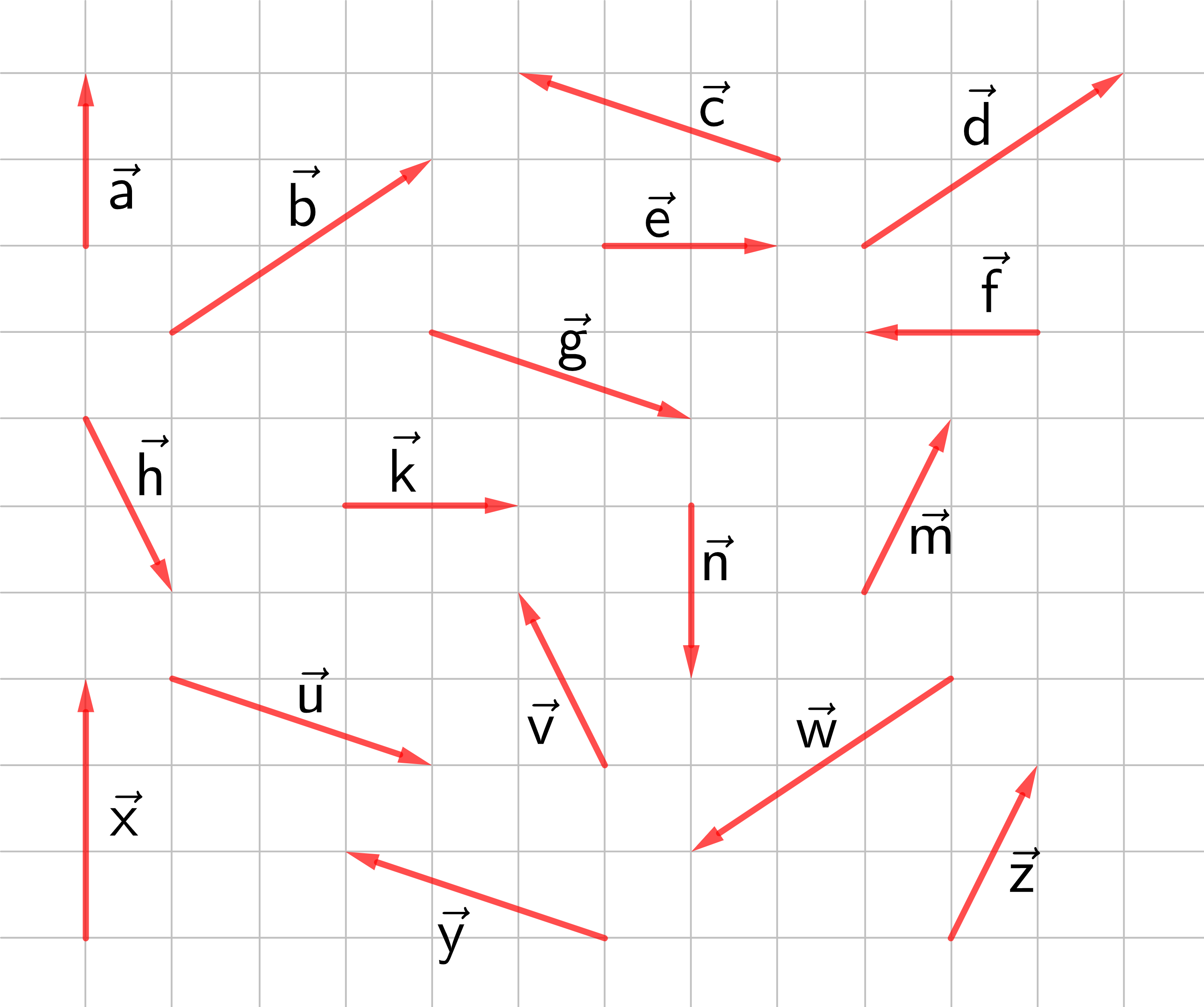
→
a
=
→
e