2. Vektorkoordinaten

← Kapitelübersicht
2.1.  Bestimmung anhand einer Zeichnung
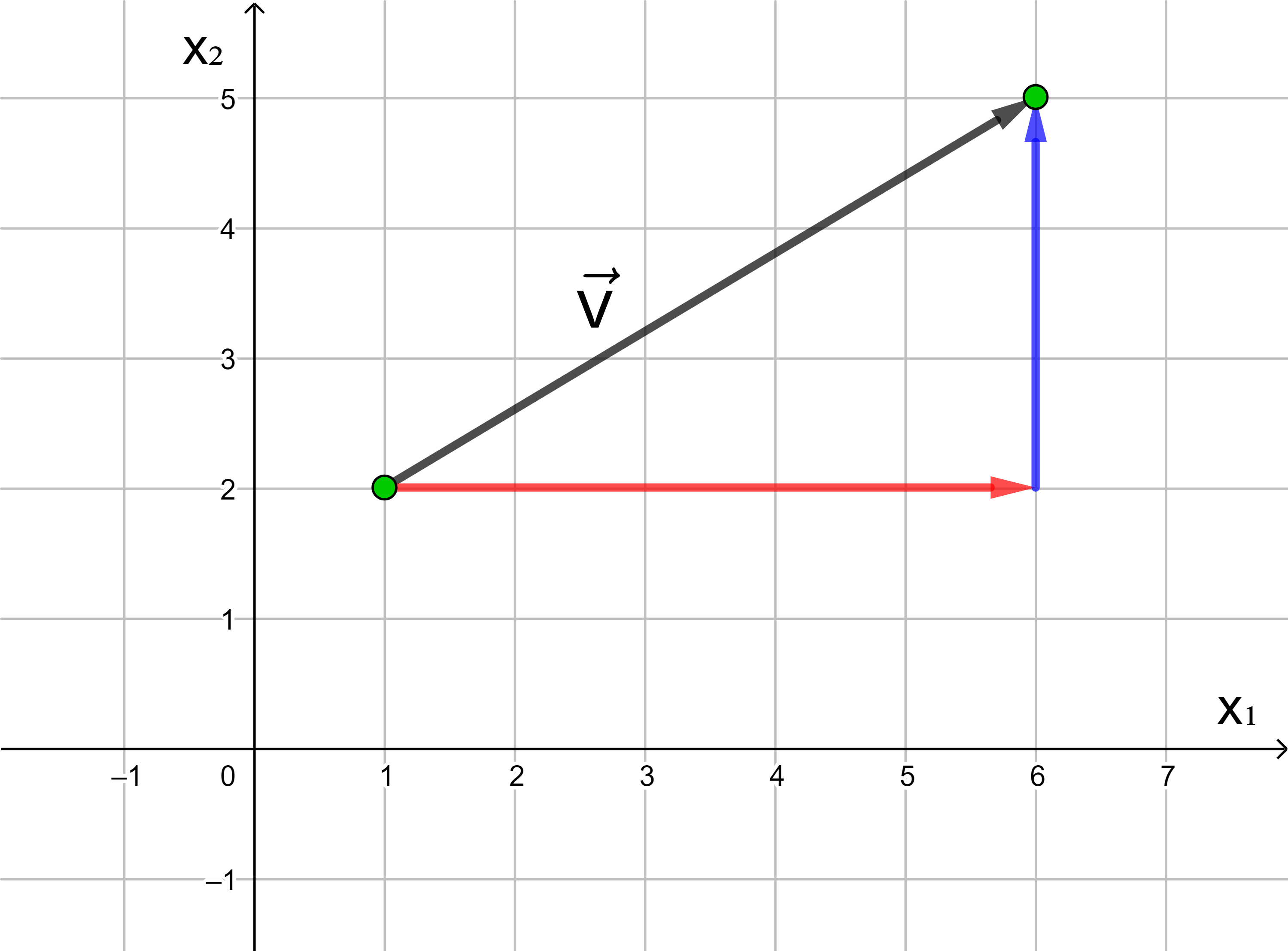
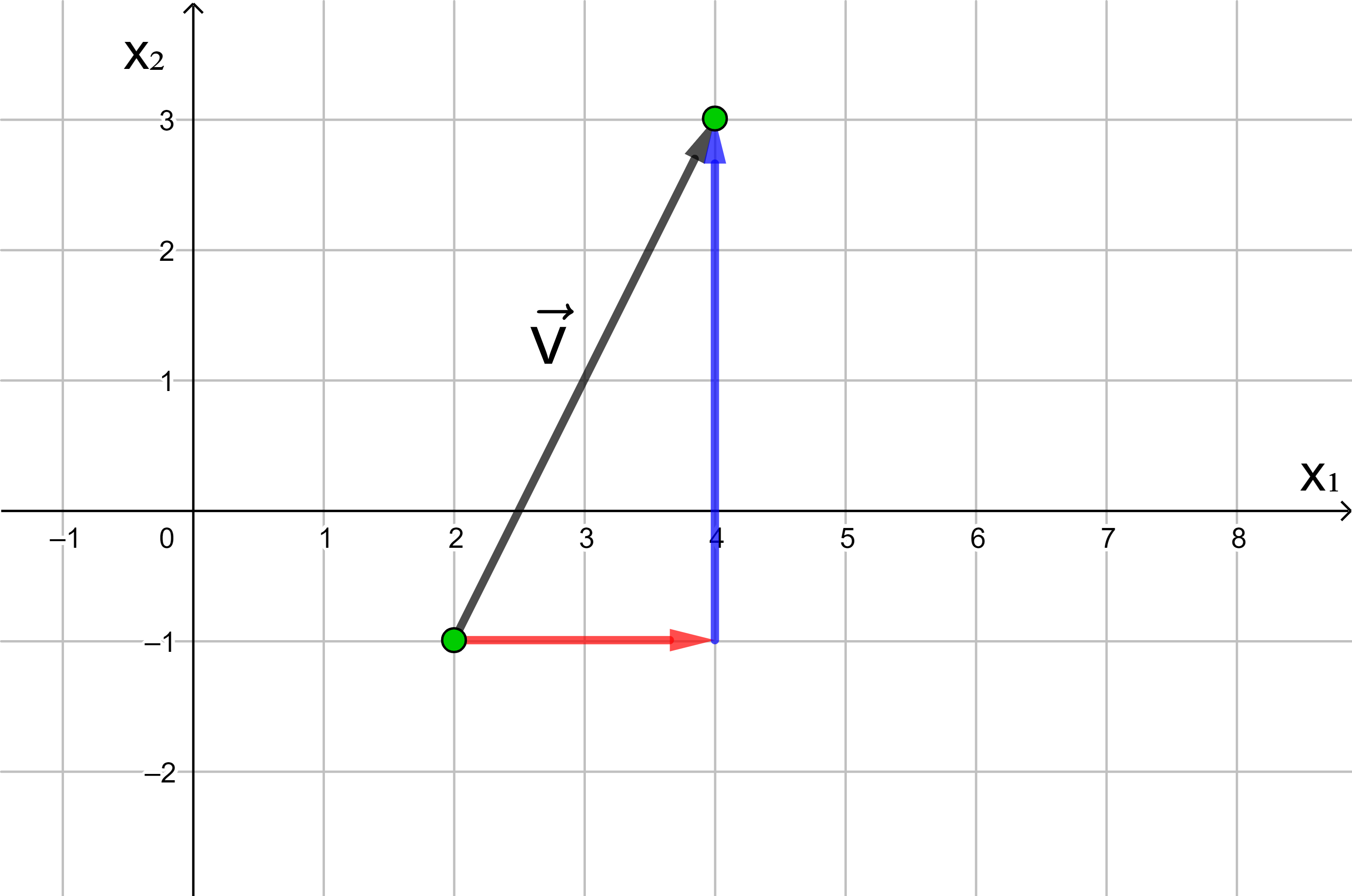
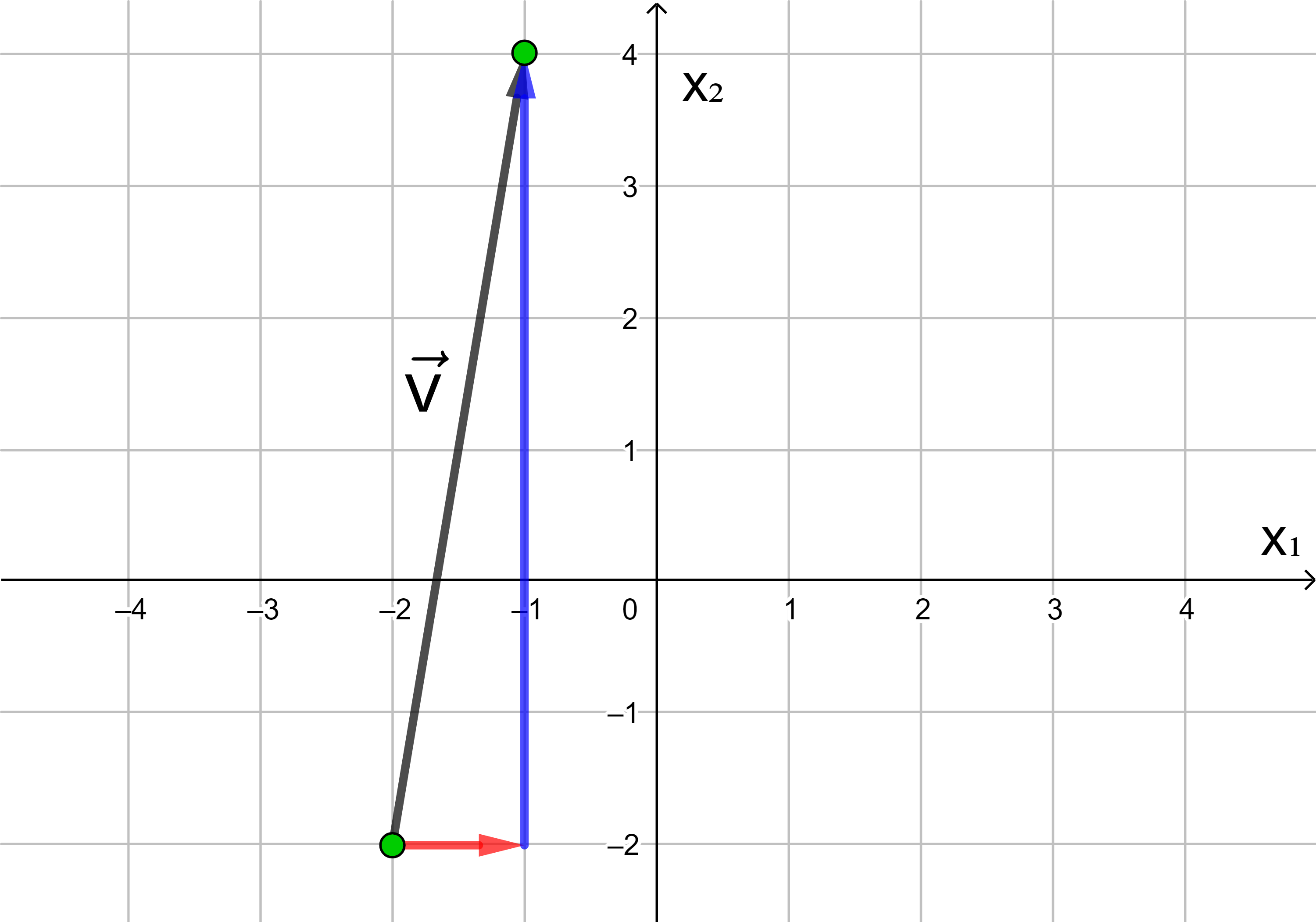
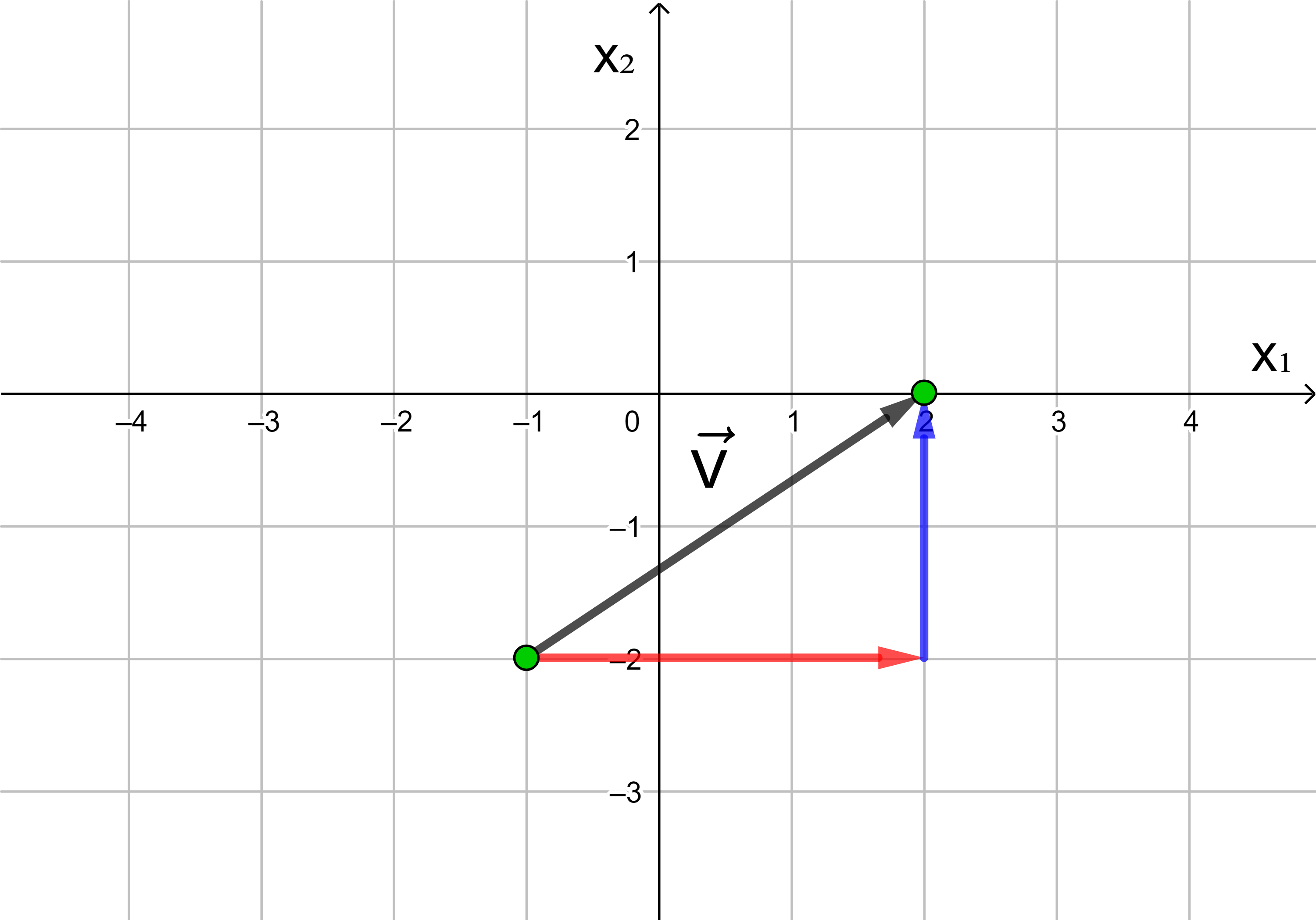
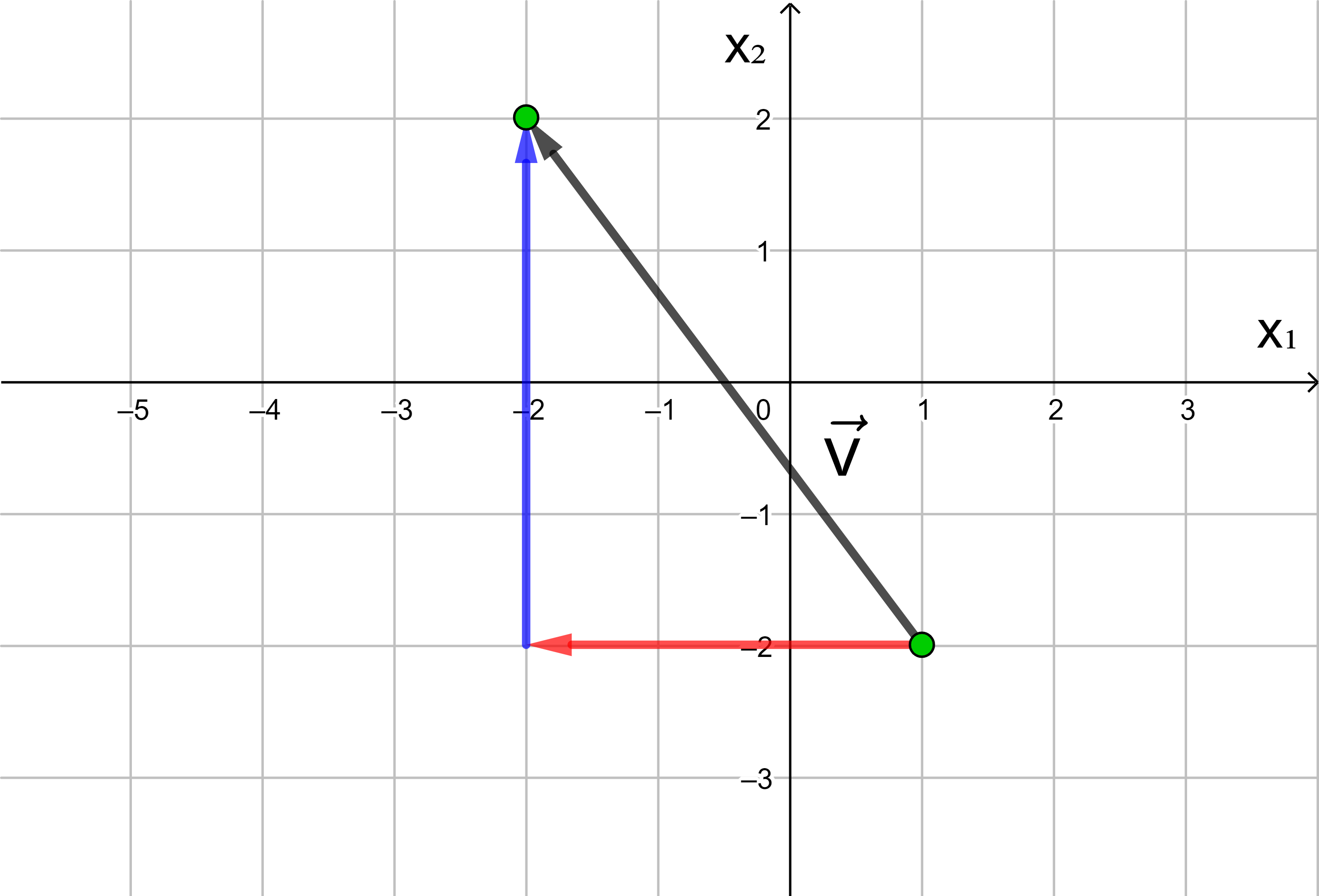
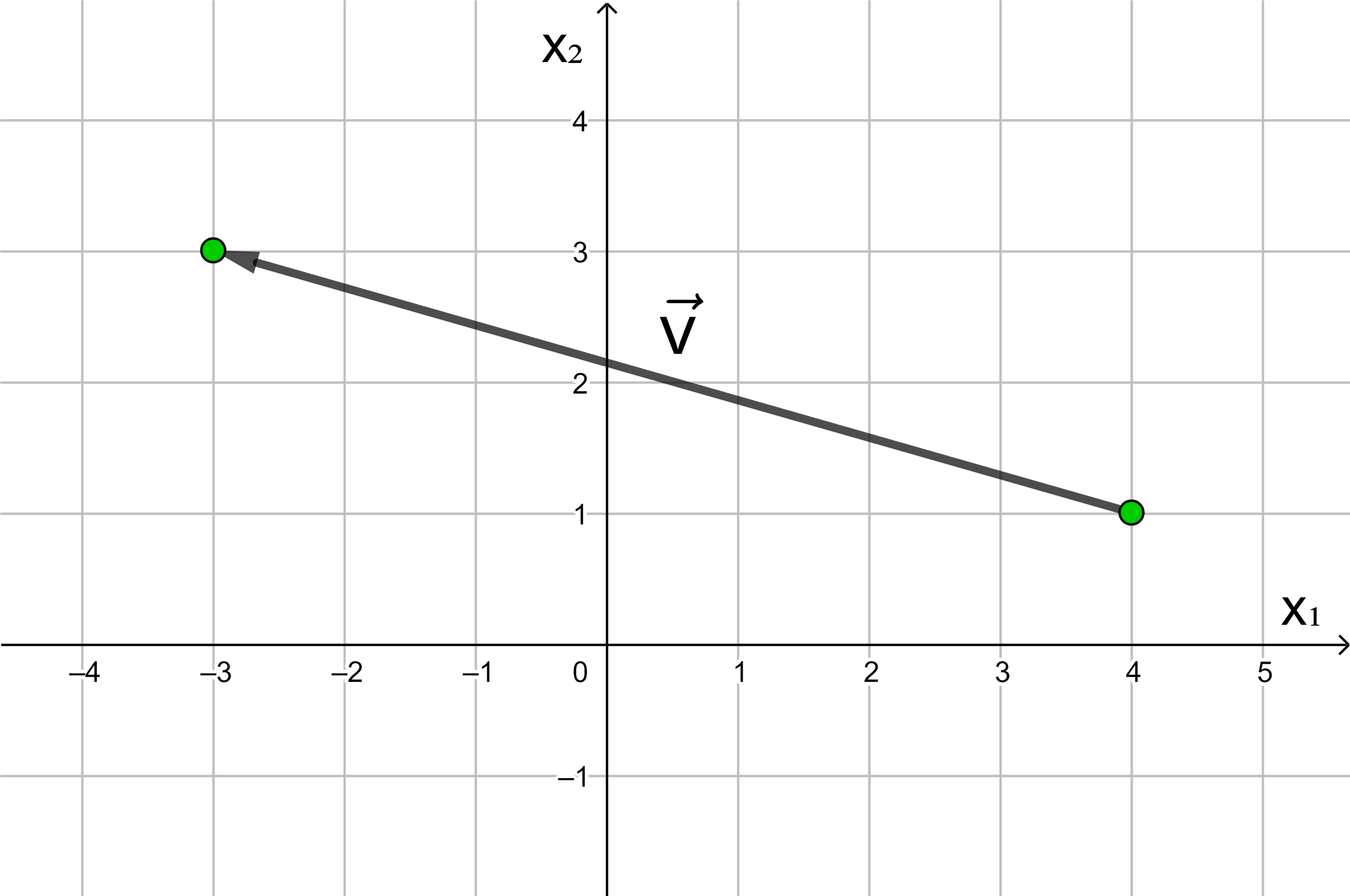
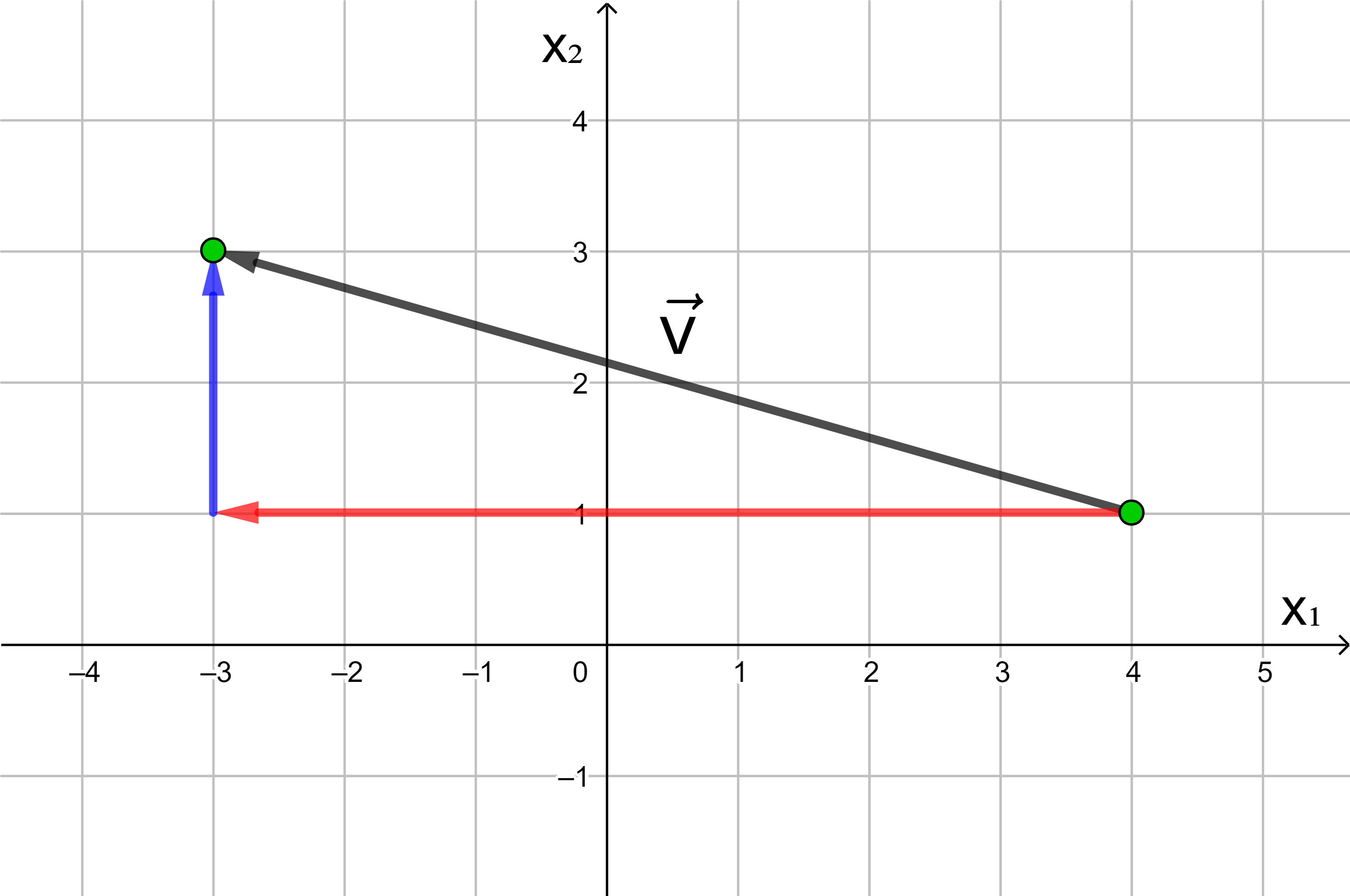
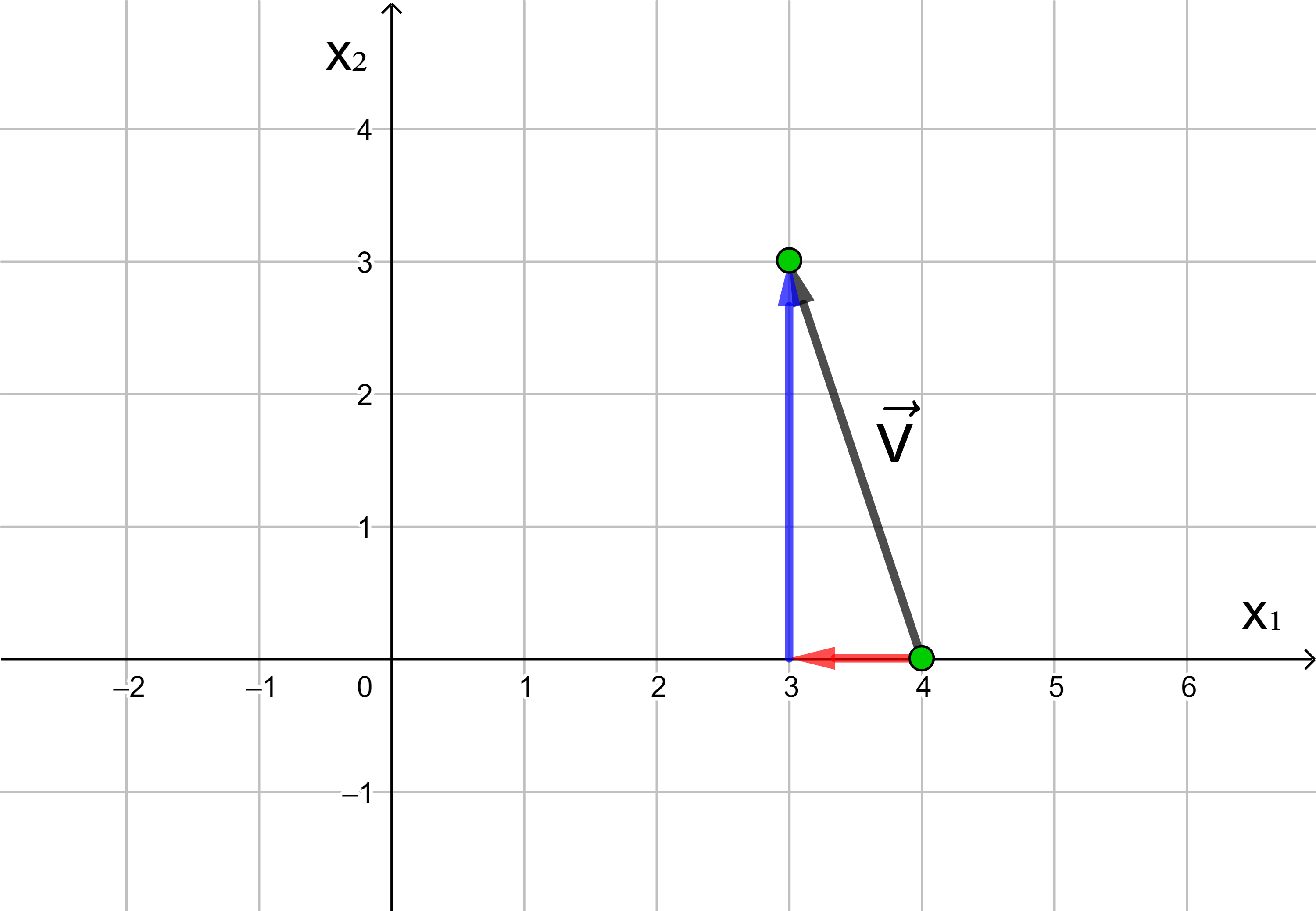
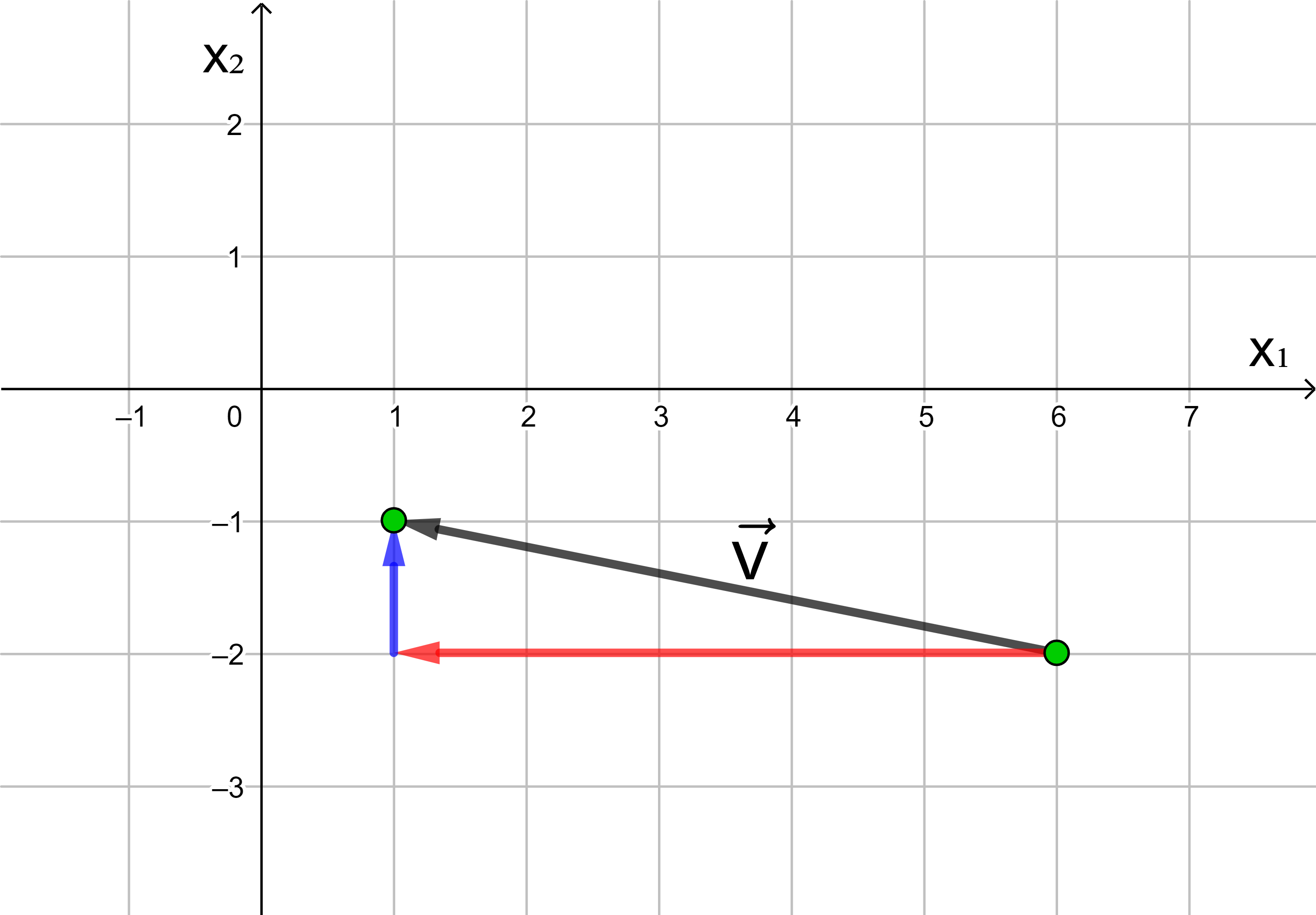
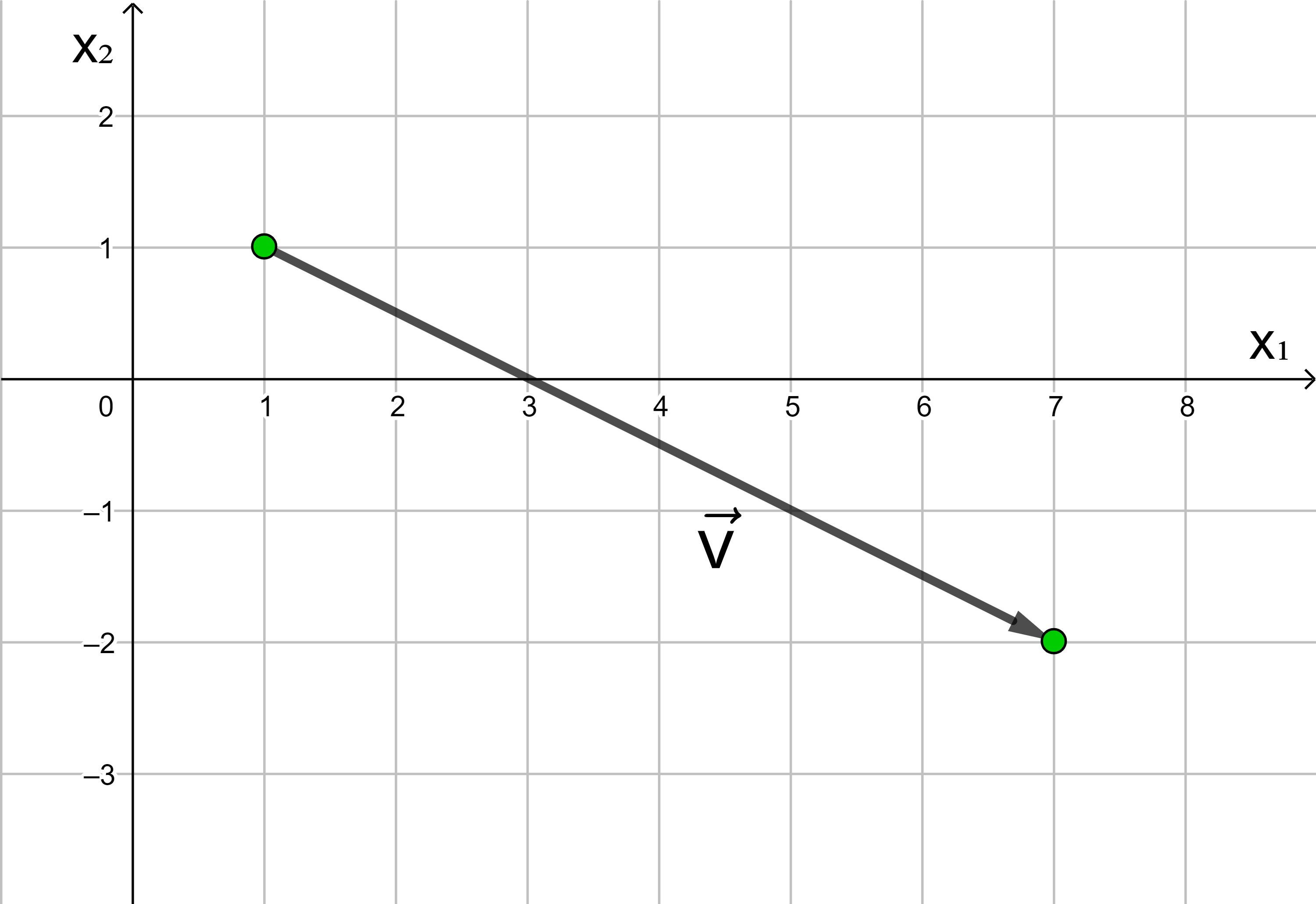
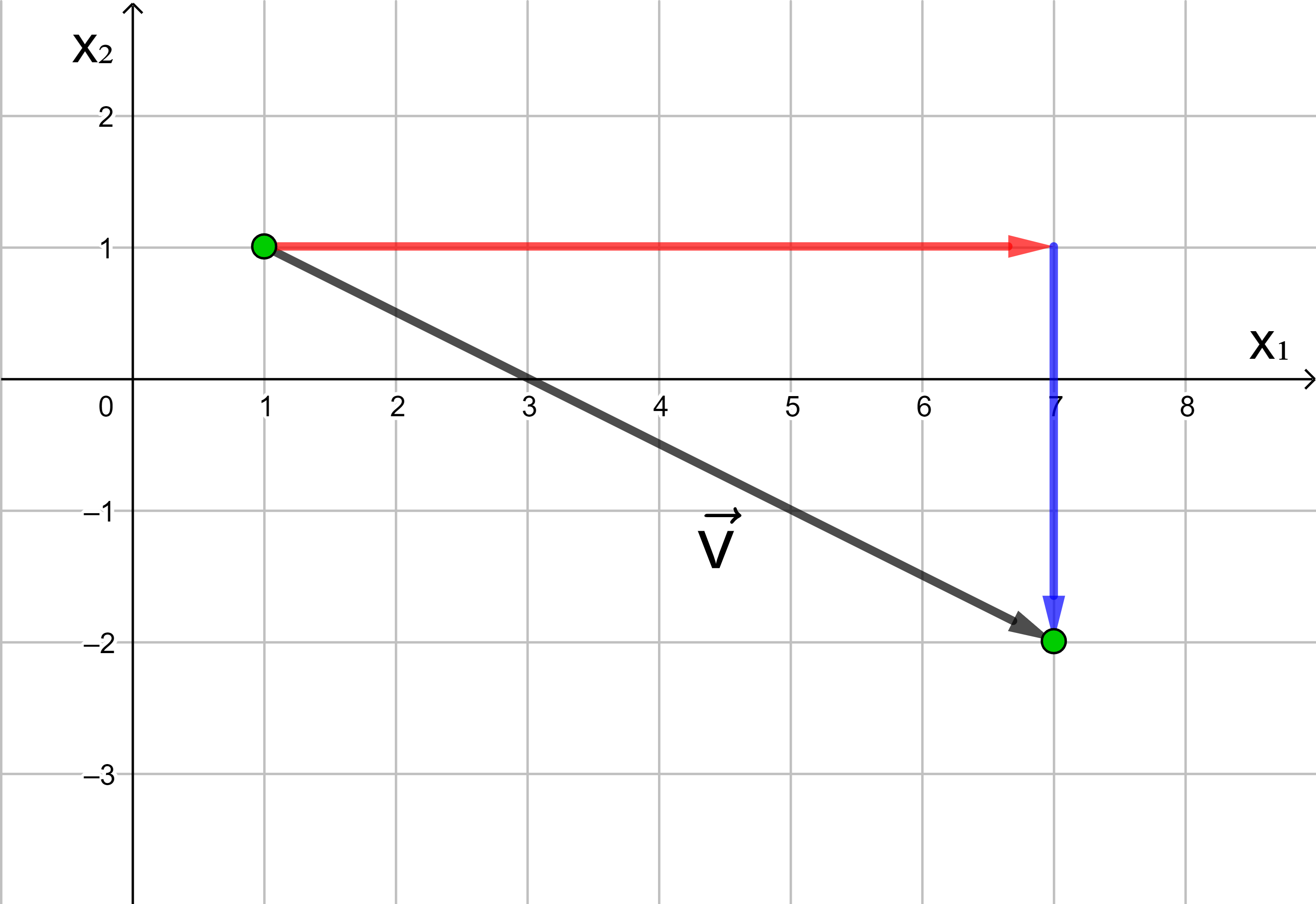
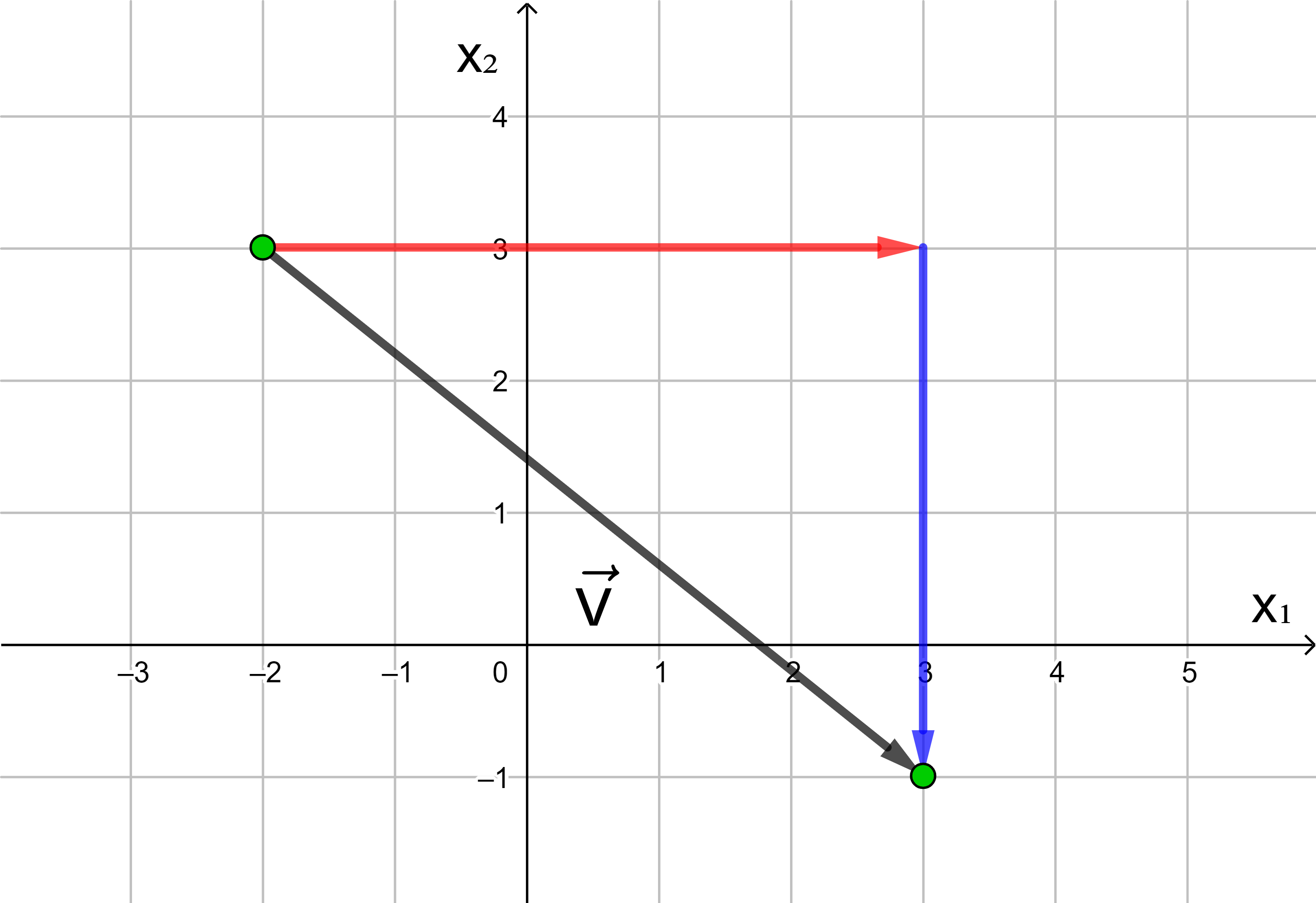
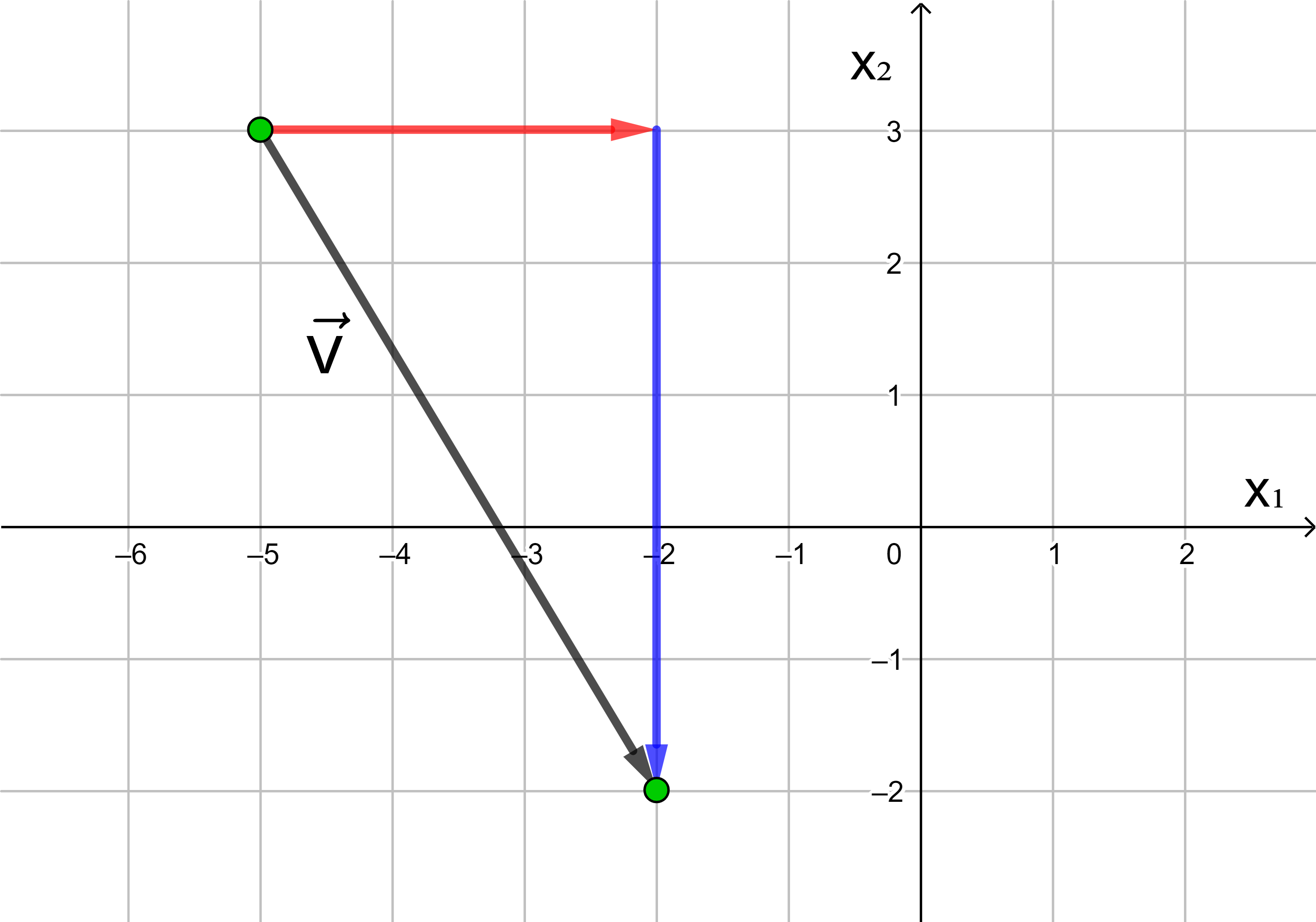
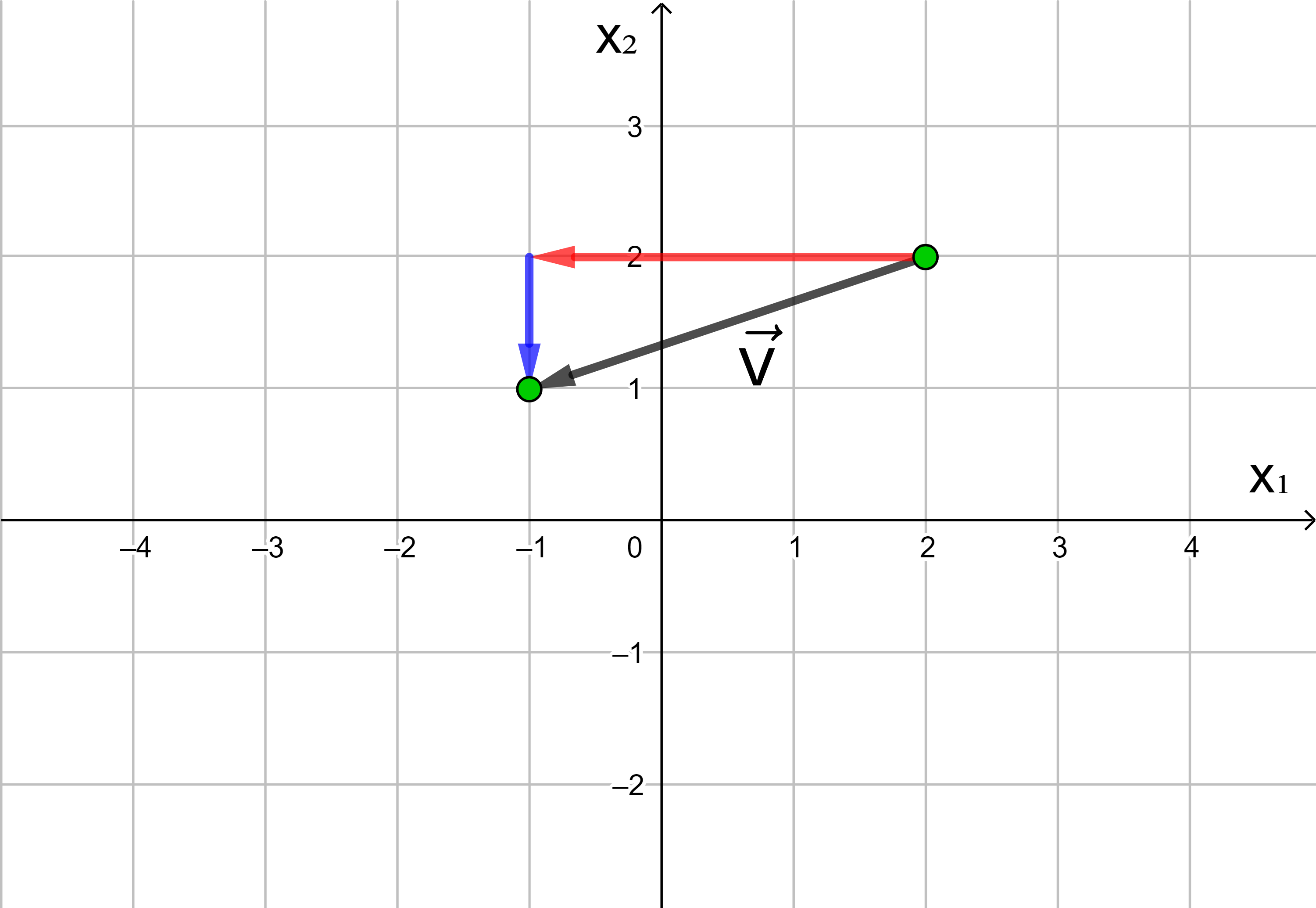
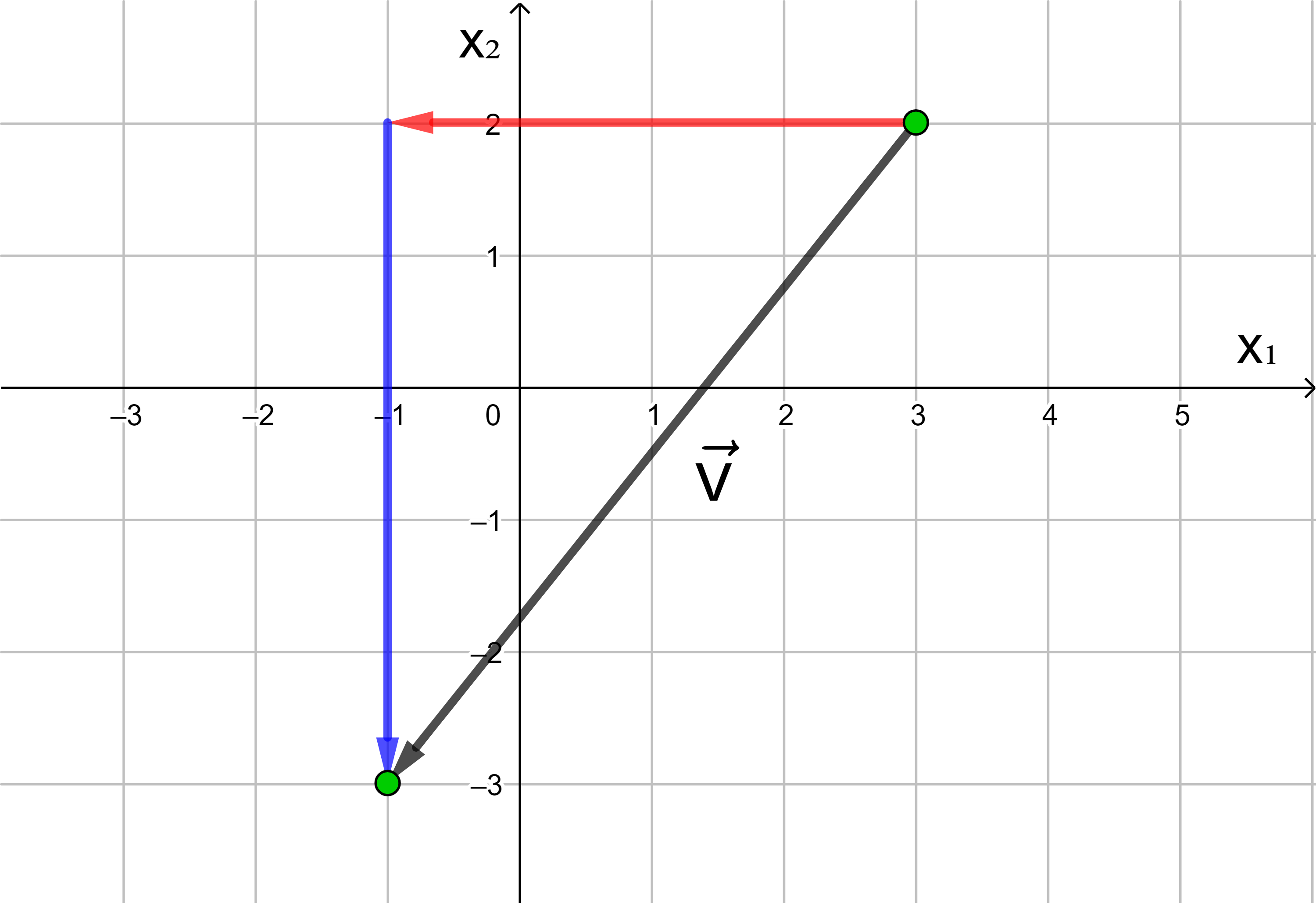
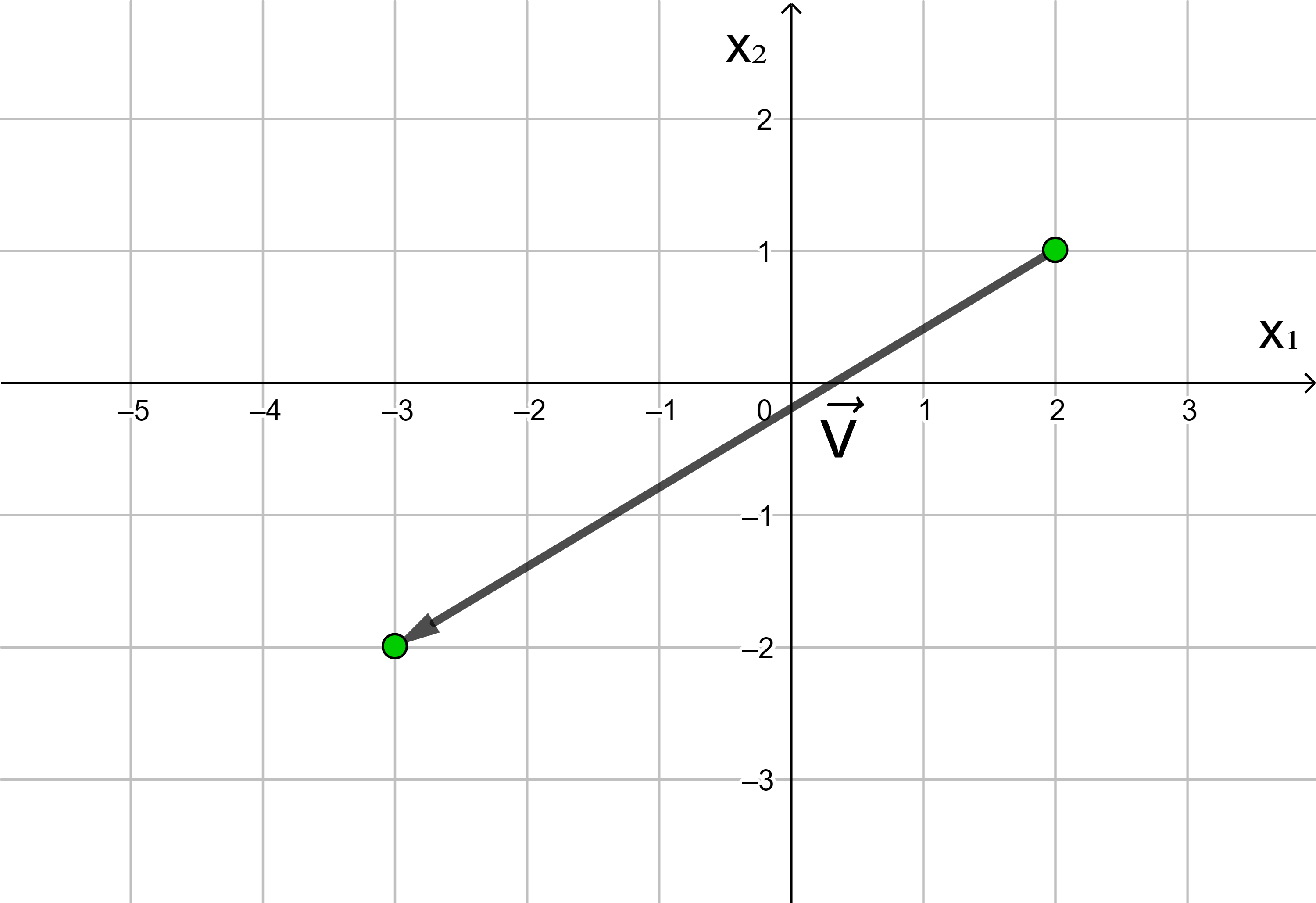
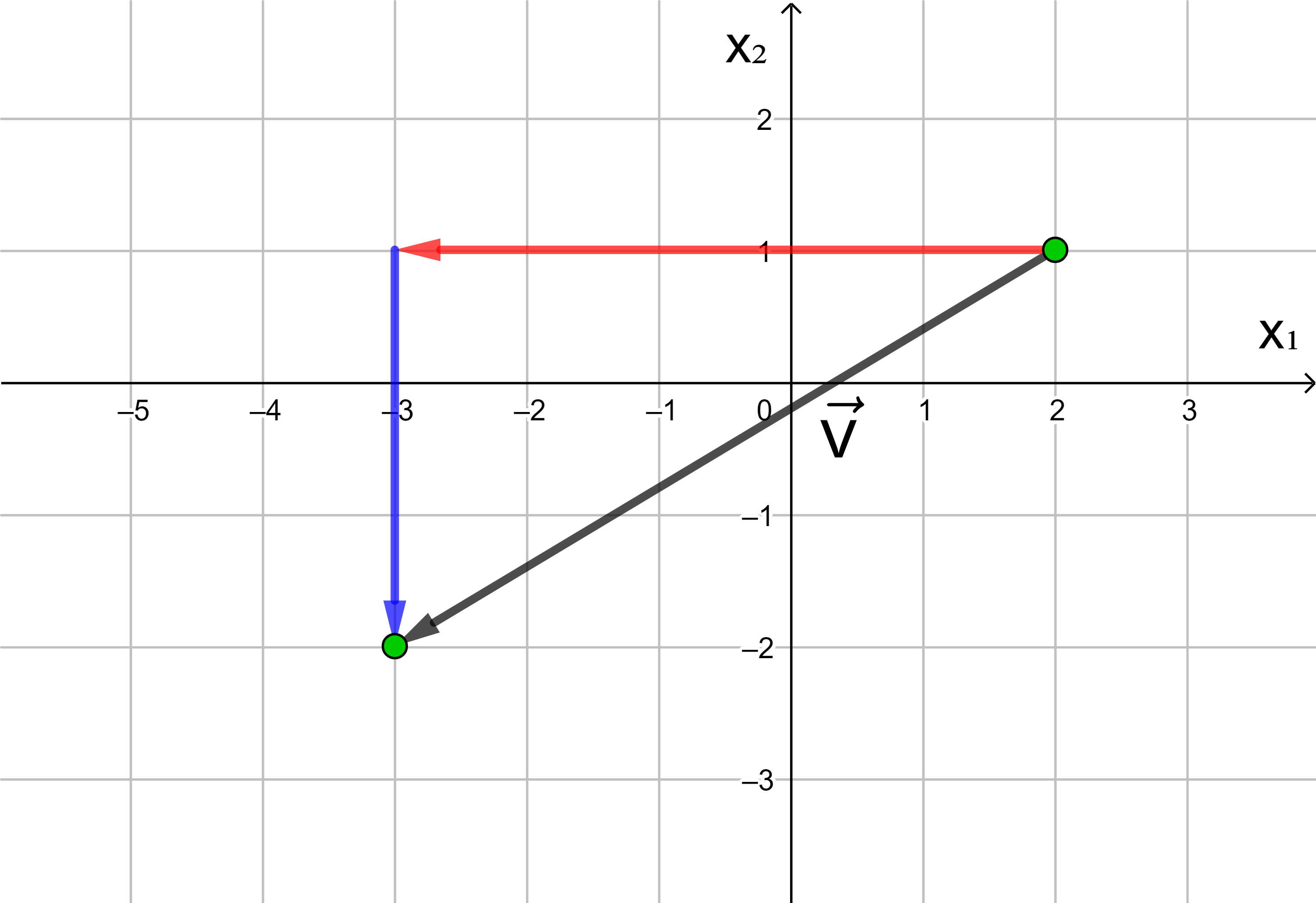
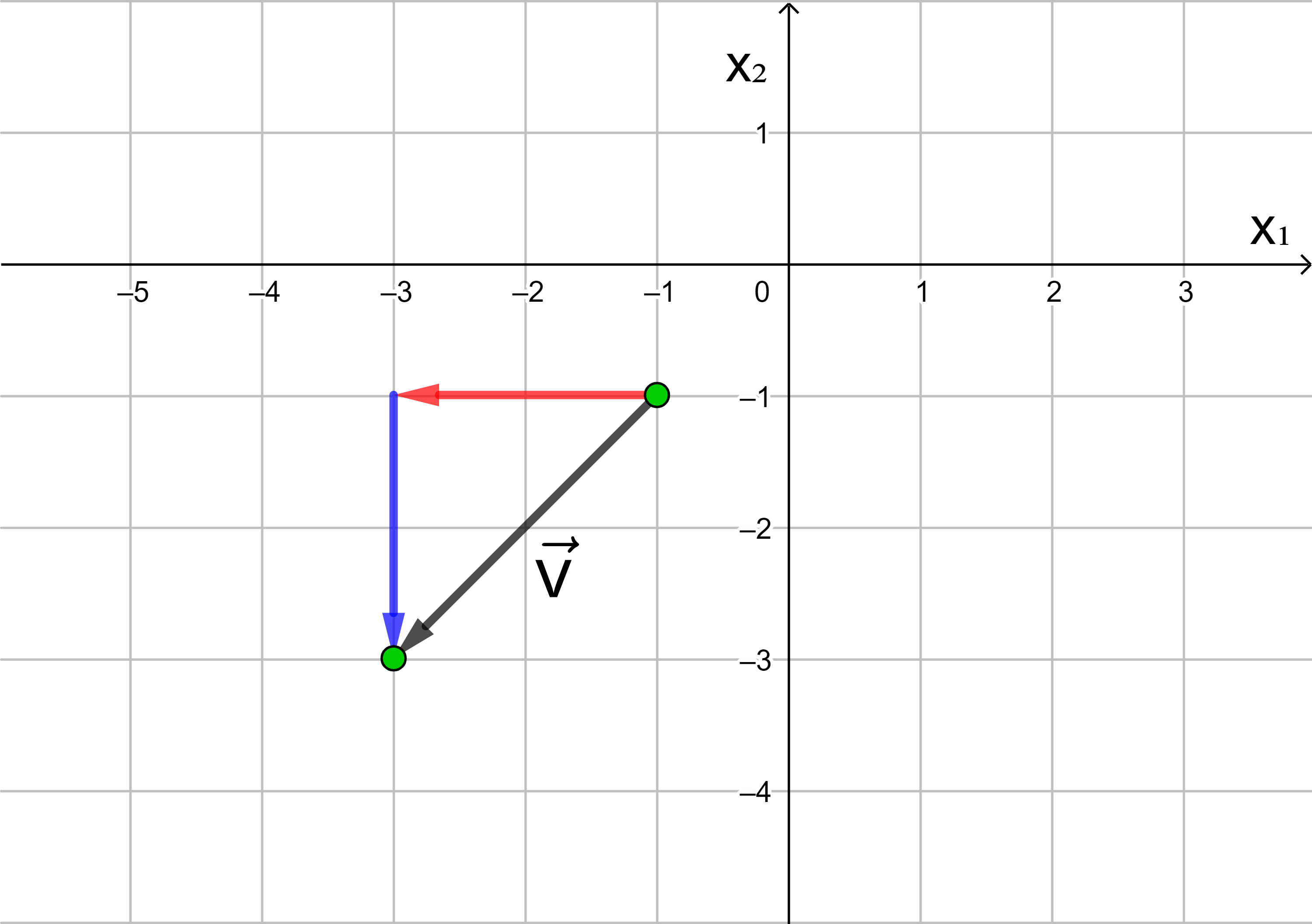
Um Vektoren voneinander unterscheiden zu können, muss man ihnen Koordinaten zuordnen. Vektoren in der Ebene benötigen zwei Koordinaten, Vektoren im Raum drei.
Jede Verschiebung eines Punktes in der Ebene kann dargestellt werden als Hintereinanderausführung einer Verschiebung in Richtung der x1-Achse und einer Verschiebung in Richtung der x2-Achse.
In der analytischen Geometrie wird die x-Achse häufig als x1-Achse und die y-Achse als x2-Achse bezeichnet.
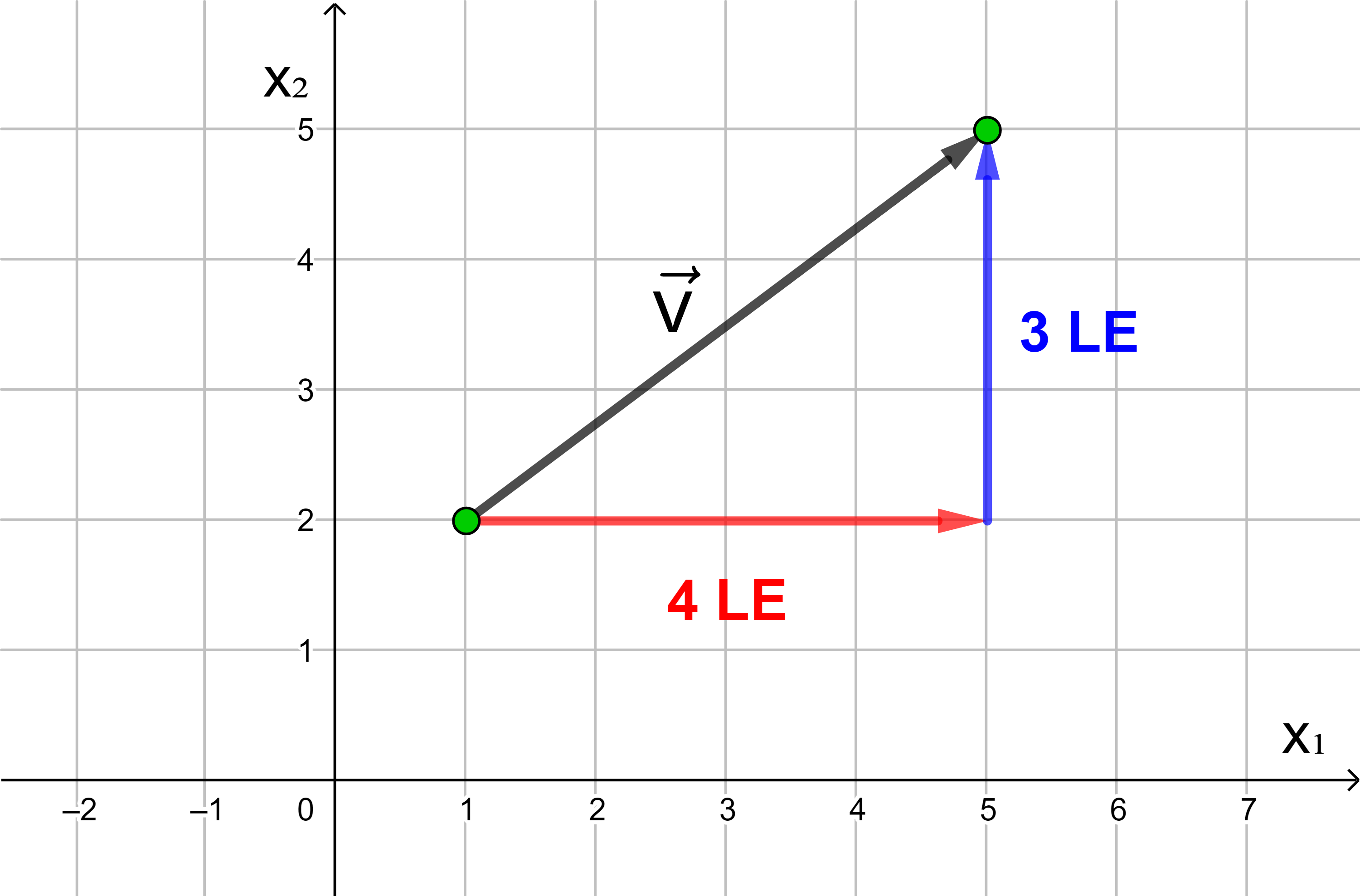
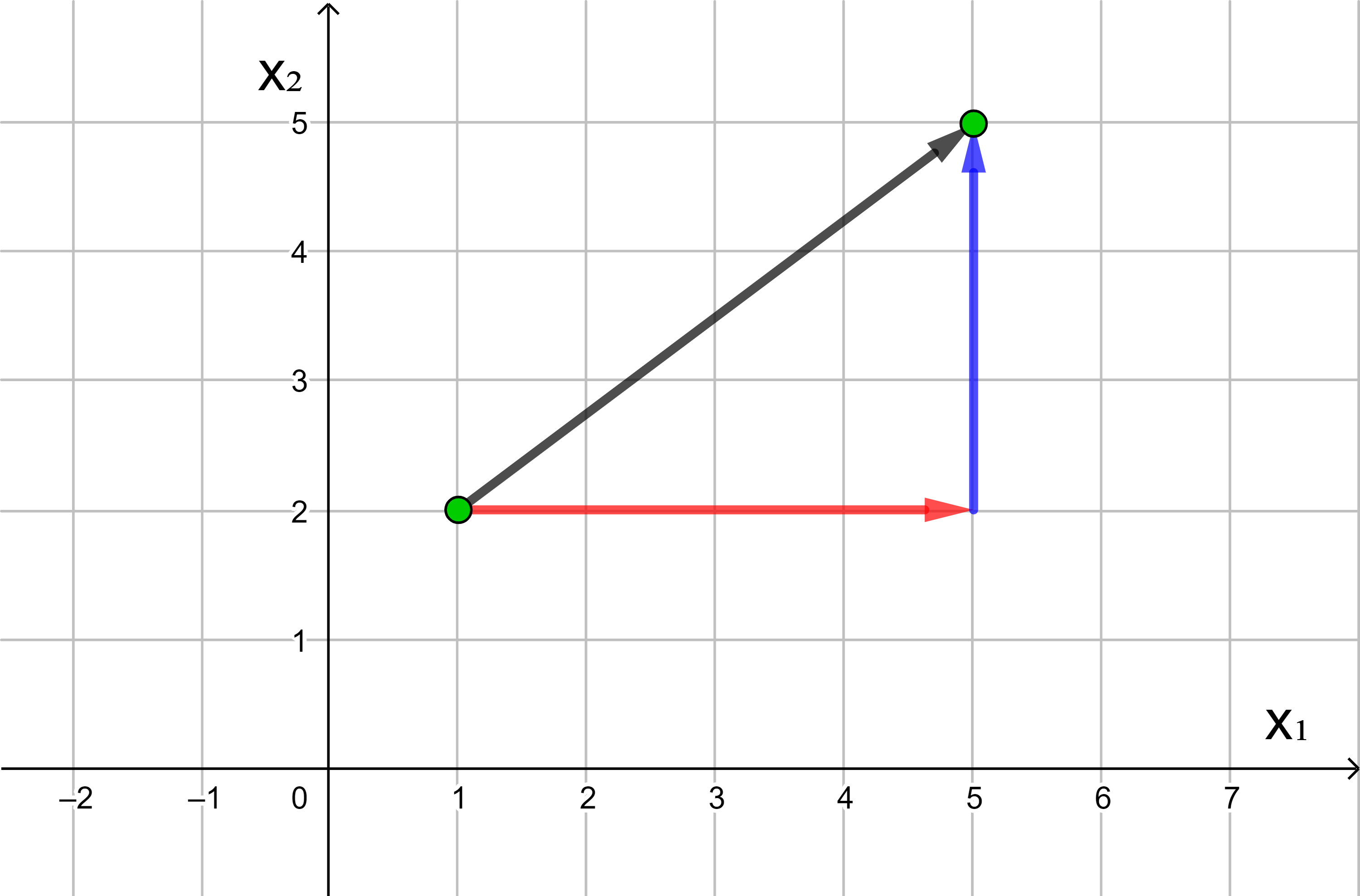
Die Anzahl der Längeneinheiten des roten und des blauen Pfeils
ergeben die Koordinaten des Vektors
→
v
.
Vektorkoordinaten schreibt man untereinander.
→
v
   =   
(
4
3
)
4 ist die x1-Koordinate, 3 die x2-Koordinate des Vektors.
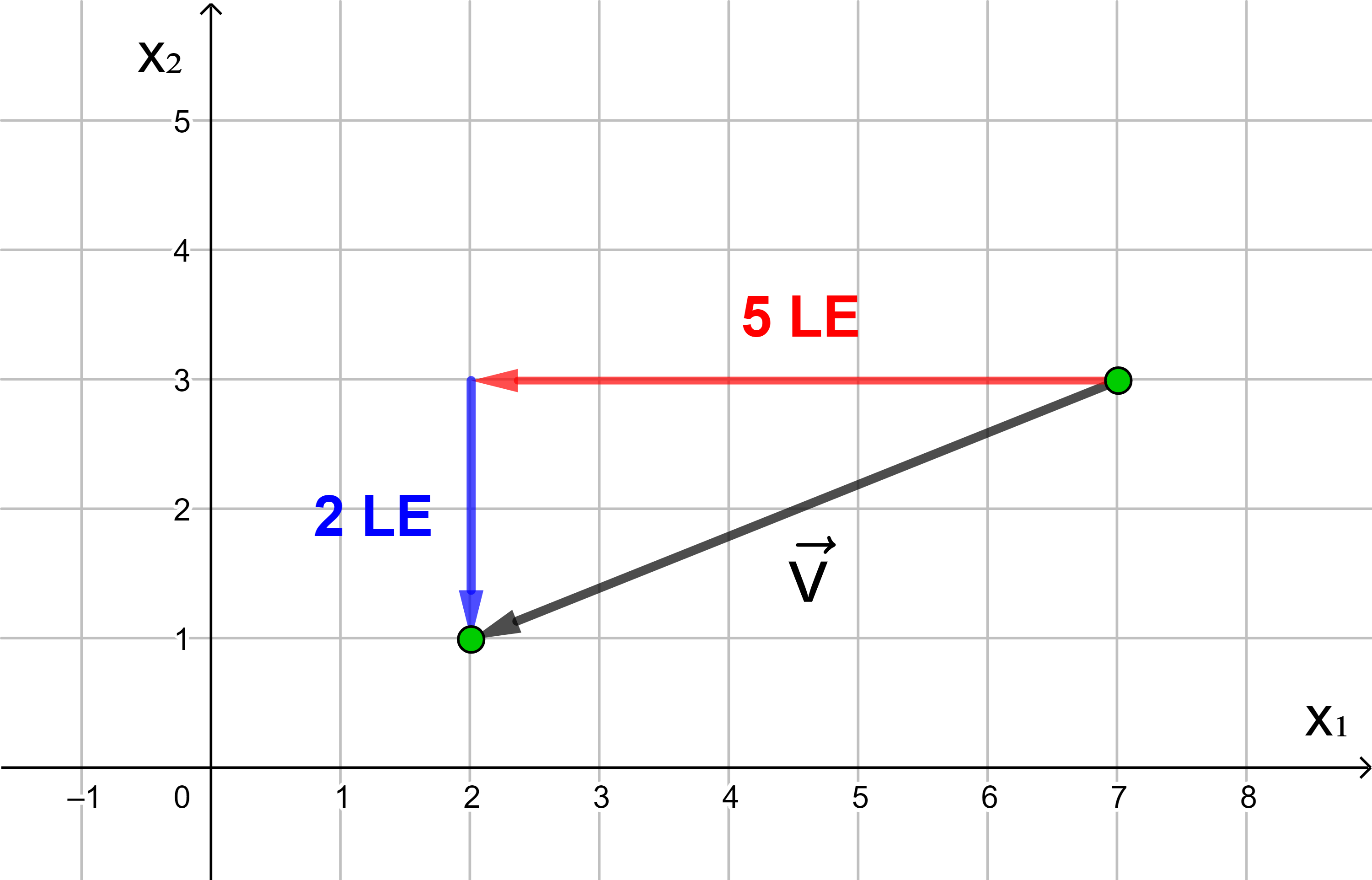
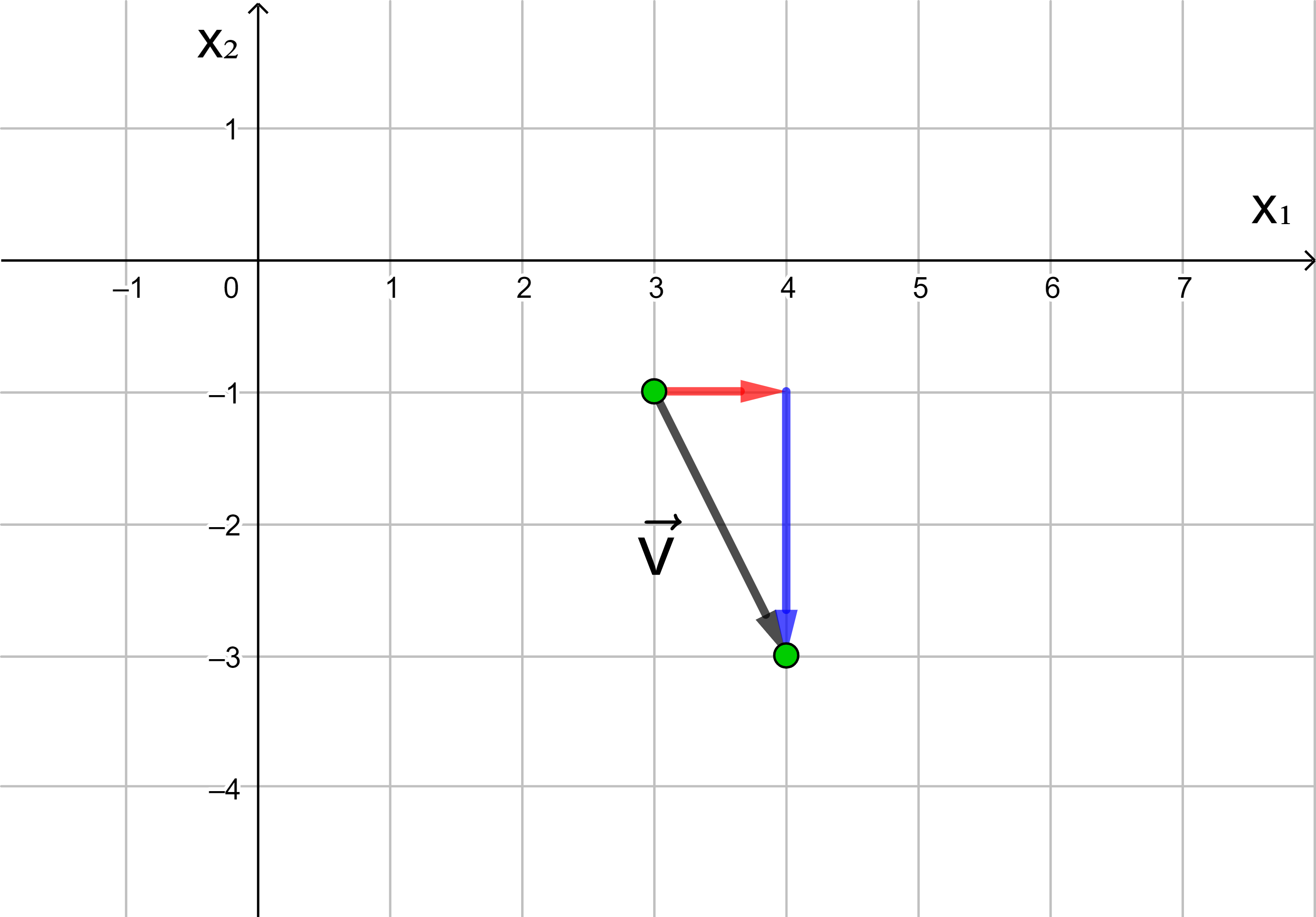
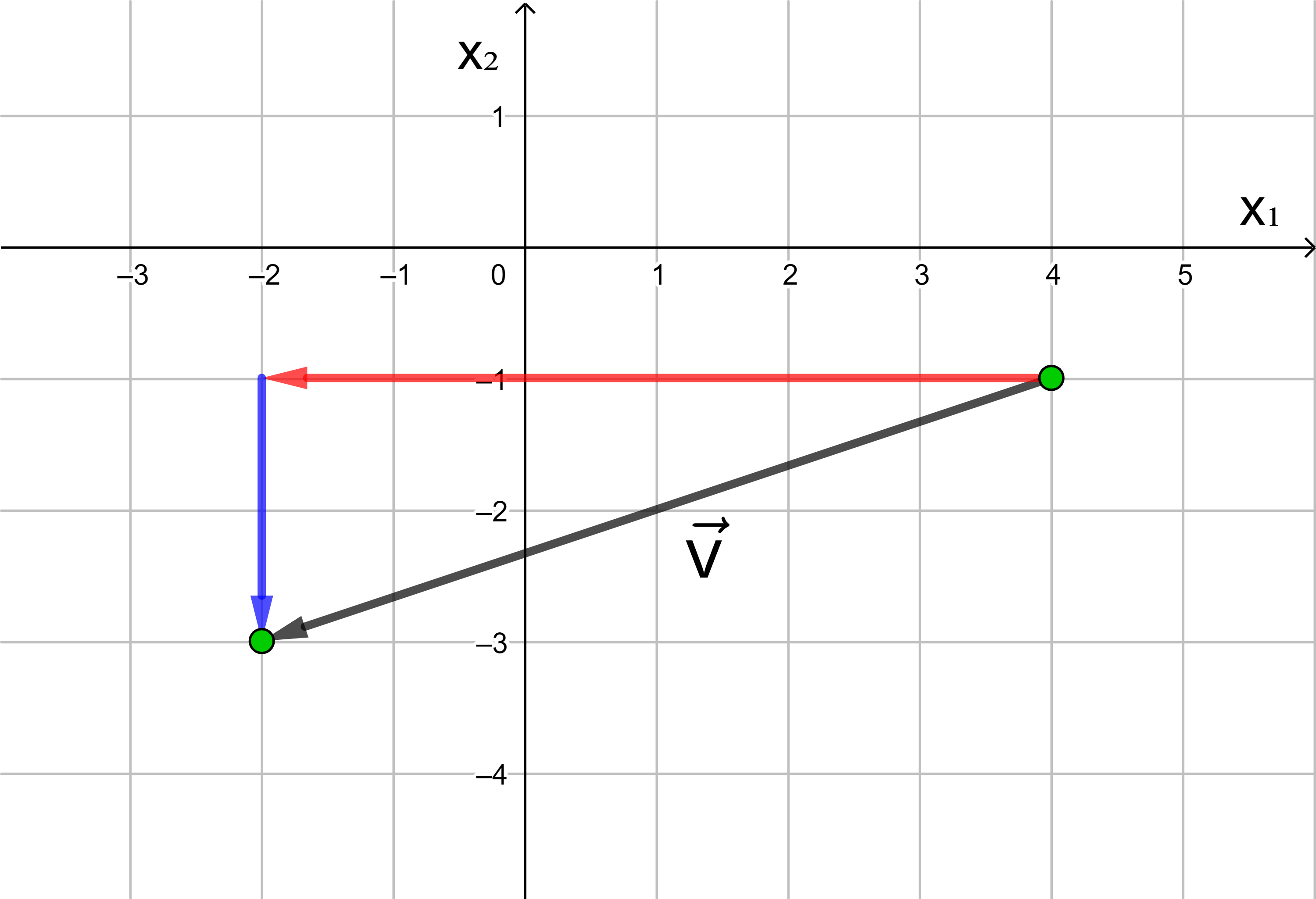
Wird ein Punkt in die negative Richtung der x1- bzw. x2-Achse verschoben, hat die x1- bzw. x2-Koordinate des Vektors ein negatives Vorzeichen.
→
v
   =   
(
− 5
− 2
)
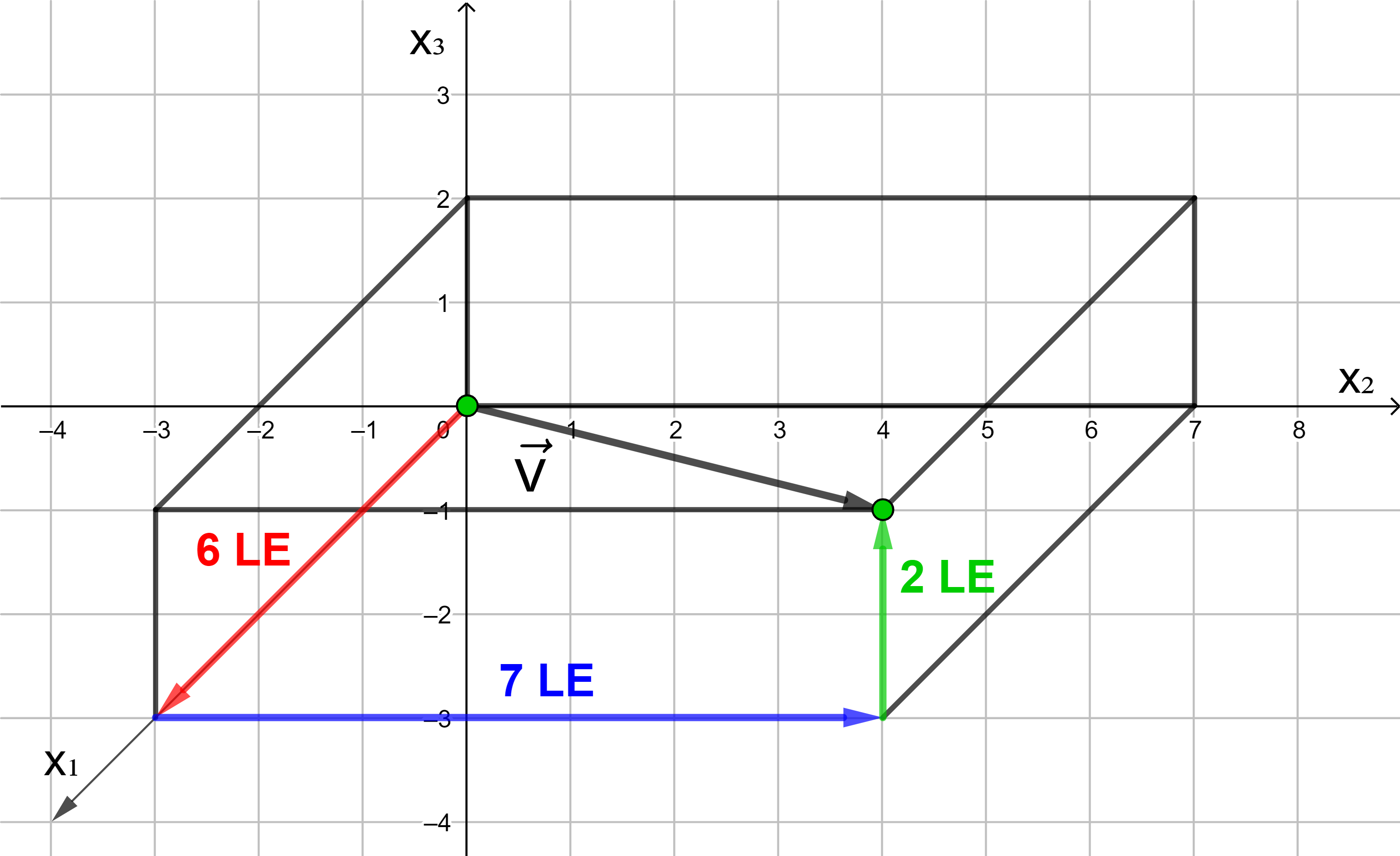
Auch Vektoren im Raum kann man Koordinaten zuweisen. Diese kann man aus einer perspektivischen Darstellung des Vektors ablesen, wenn der Vektor auf einer Diagonalen eines Koordinatenquaders liegt. Die Kanten des Quaders verlaufen parallel zu den Koordinatenachsen.
→
v
   =   
(
6
7
2
)
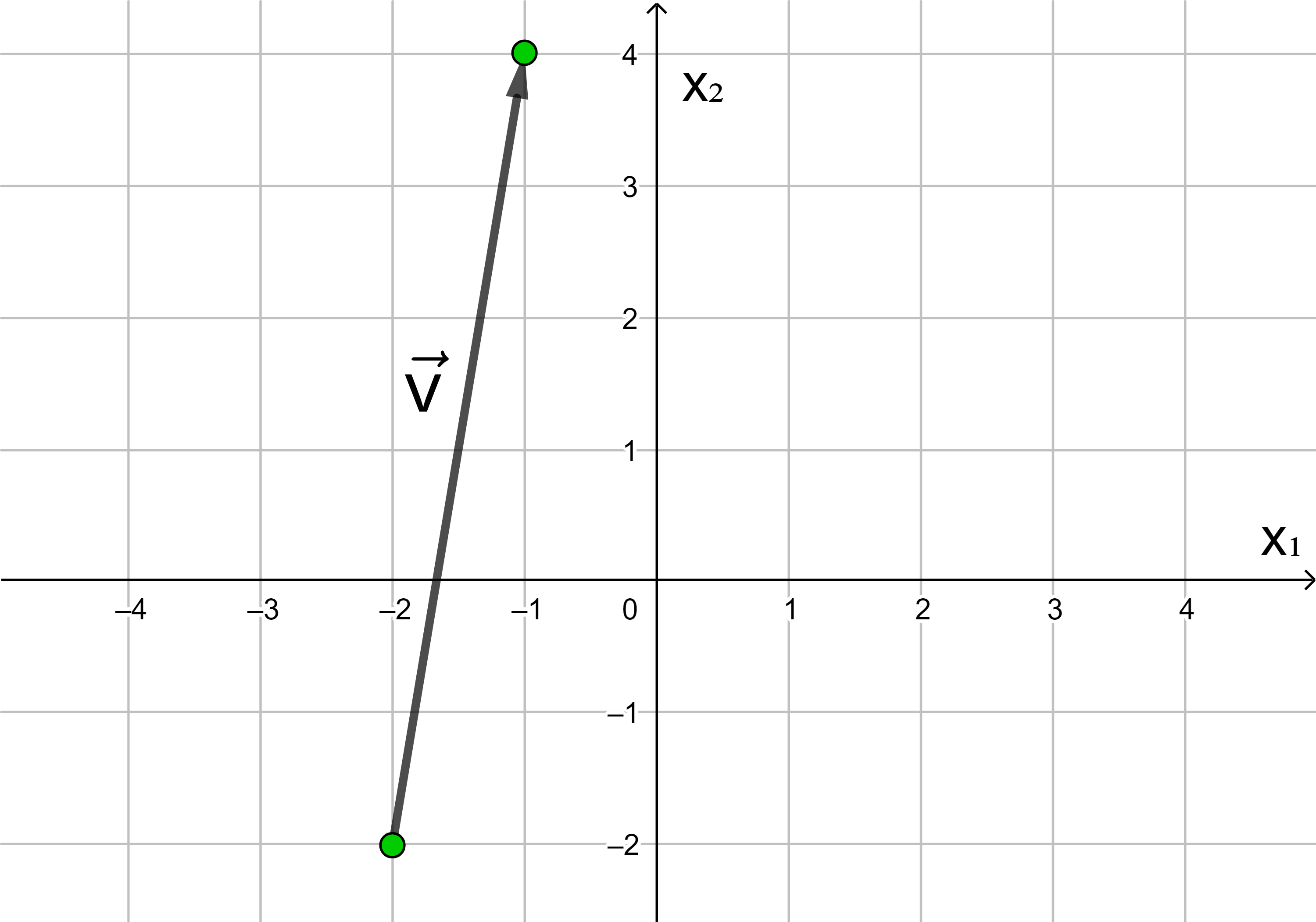
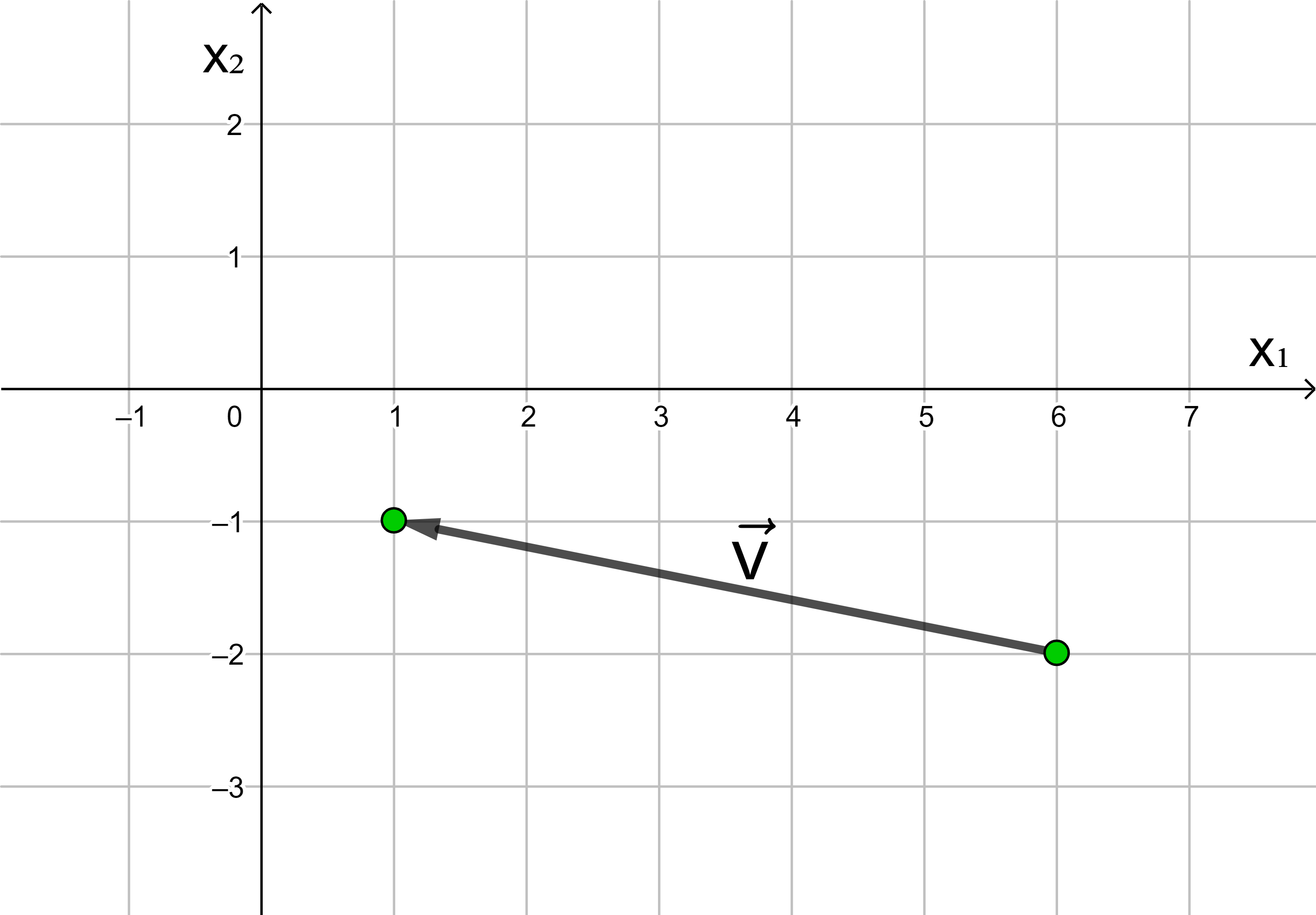
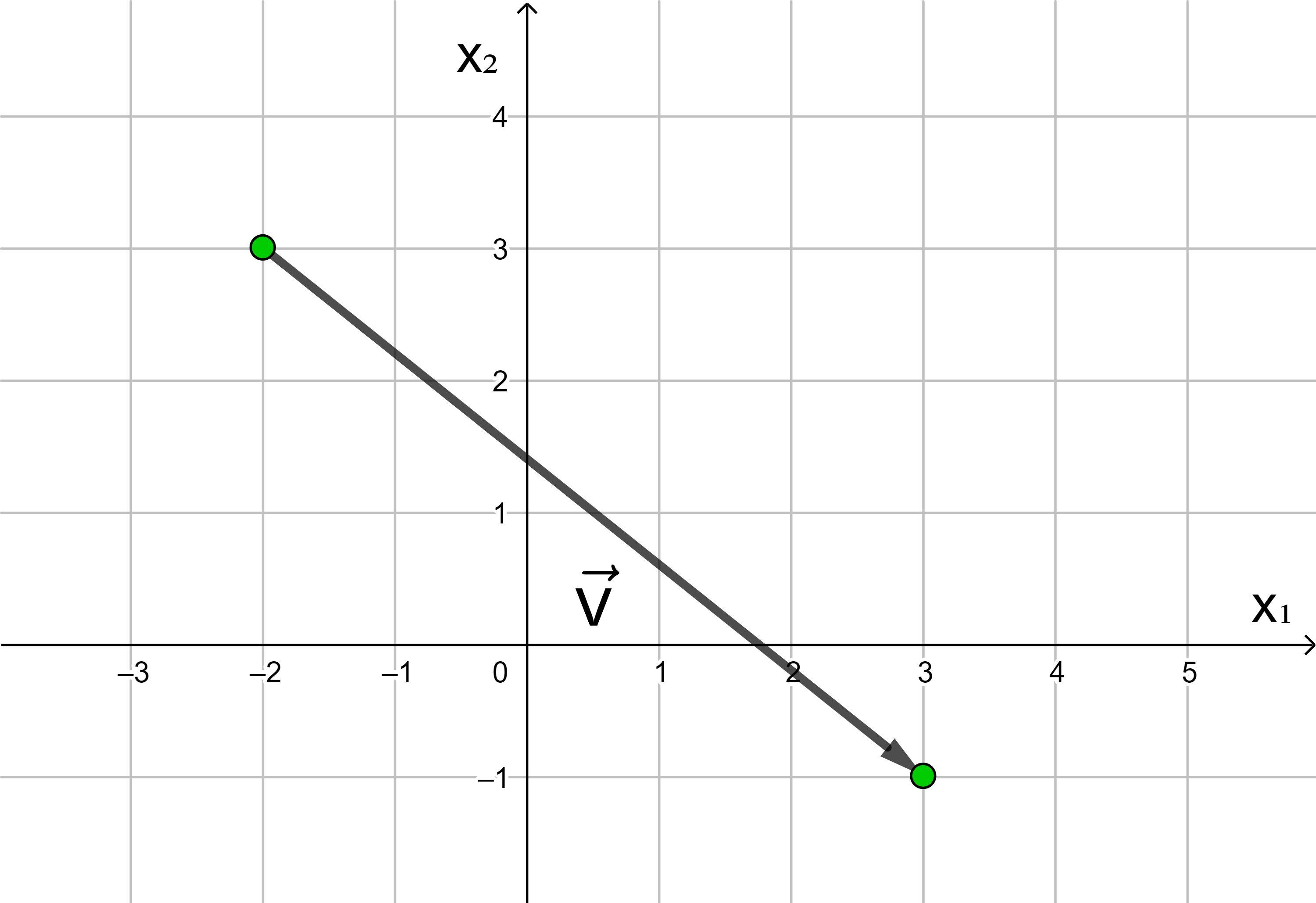
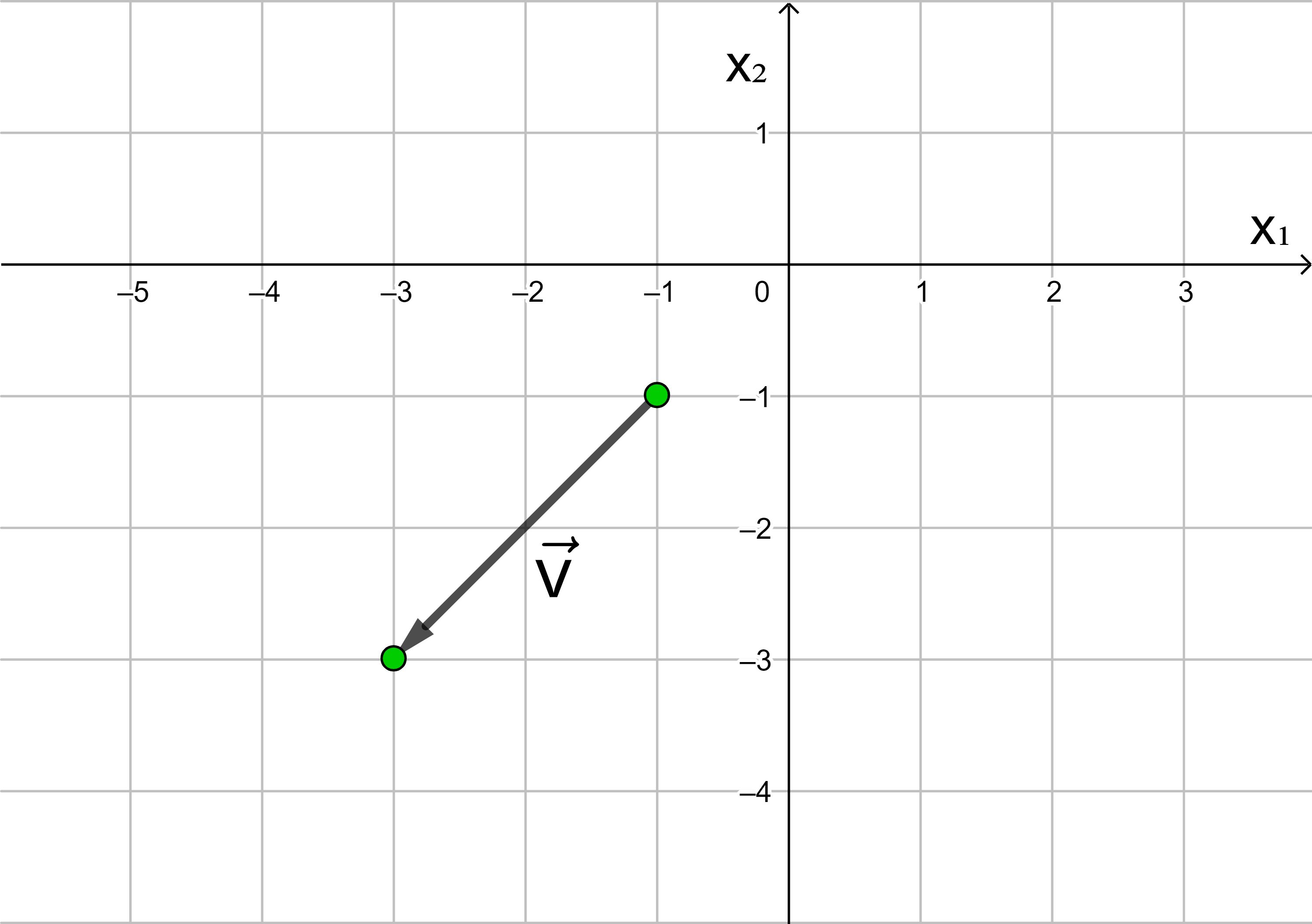
Übung:
Geben Sie die Koordinaten des in der Zeichnung dargestellten Vektors in die dafür vorgesehenen Felder ein. Rufen Sie, falls nötig, eine Hilfestellung auf. Kontrollieren Sie Ihr Ergebnis oder lassen Sie sich die Lösung anzeigen.
→
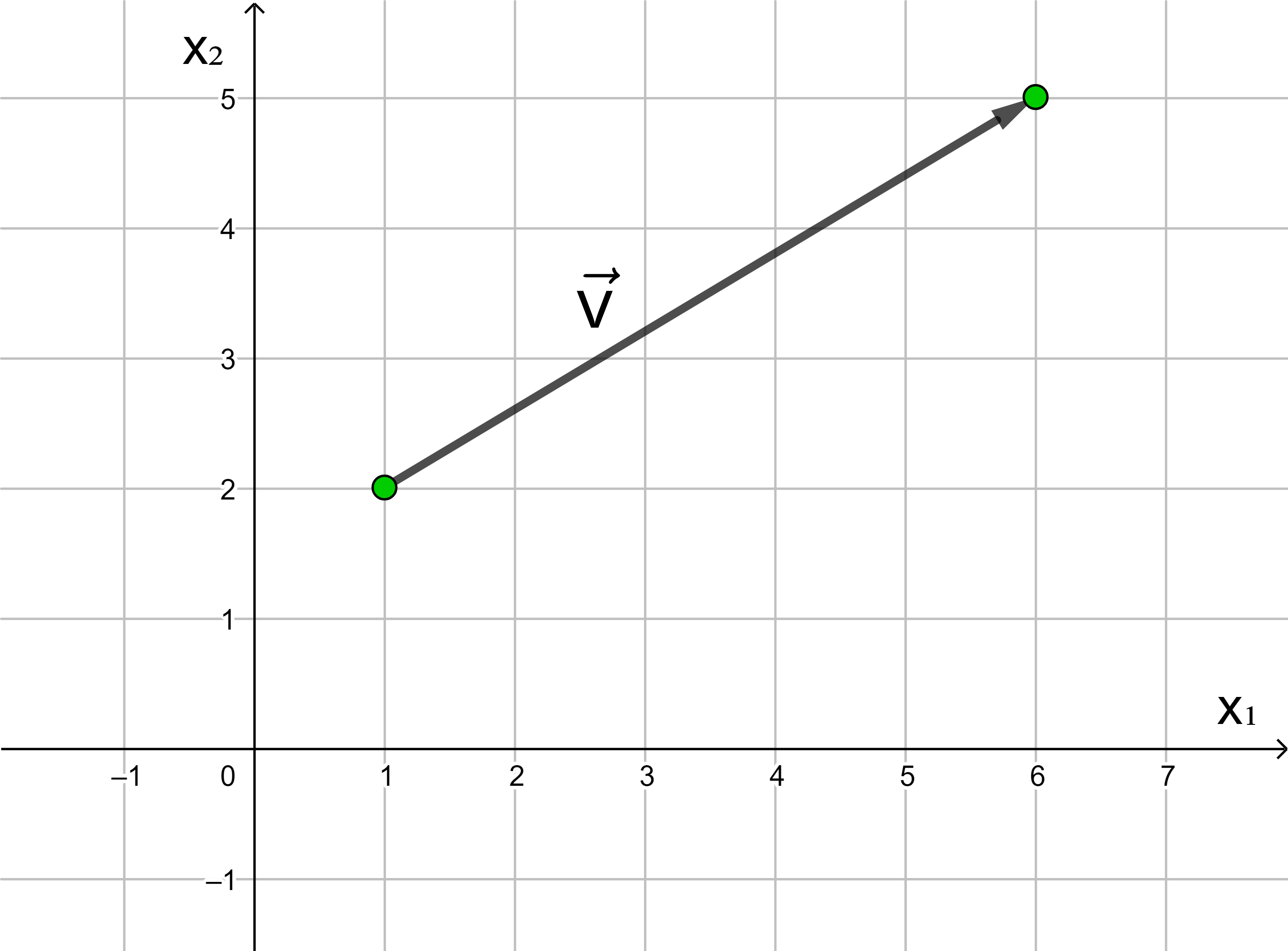
v
   =   
(
)
Kontrolle
Hilfe
Lösung
Neue Aufgabe
1. ← → 2.2.