2. Vektorkoordinaten
← Kapitelübersicht2.2. Berechnung mit Hilfe von Punktkoordinaten
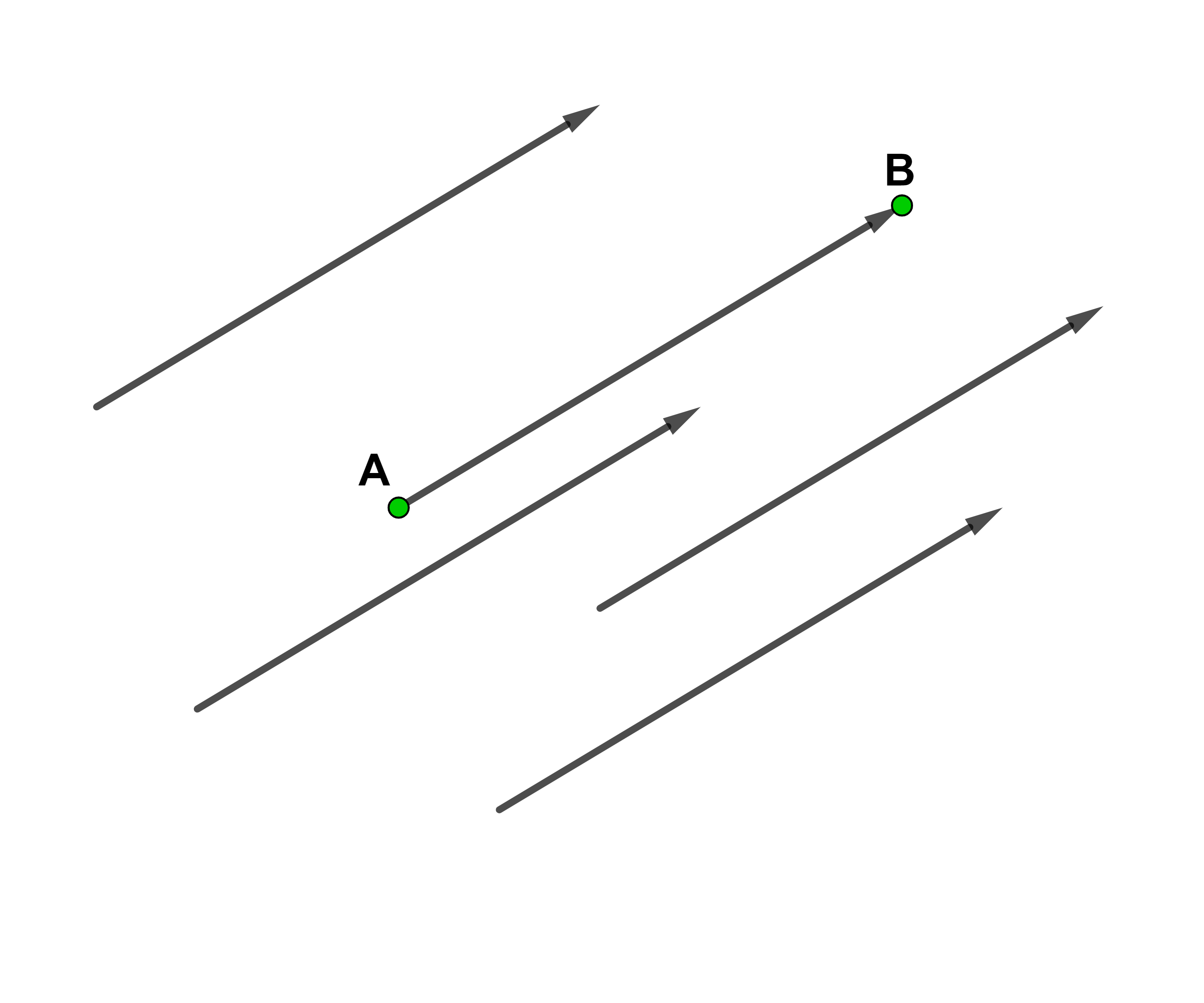
Ein Vektor ist durch unendlich viele parallele, gleich lange und gleich orientierte Pfeile darstellbar.
Kennt man die Koordinaten des Anfangs- und des Endpunktes eines einzigen Pfeiles, kann man die Koordinaten des Vektors berechnen.
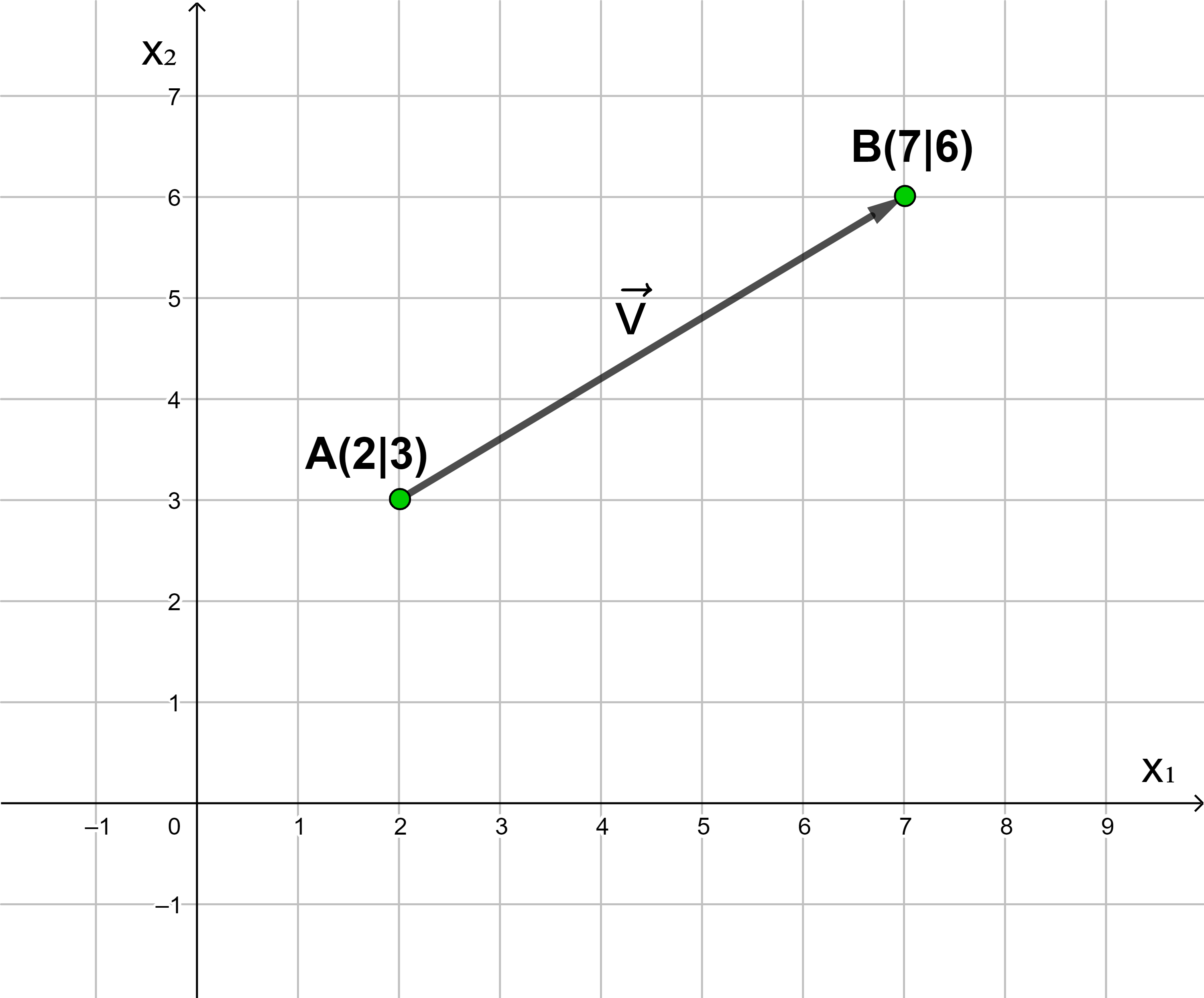
Der Vektor, der einen Punkt von A nach B verschiebt, heißt Verbindungsvektor der Punkte A und B.
Man schreibt:
→
v
=
⟶
AB
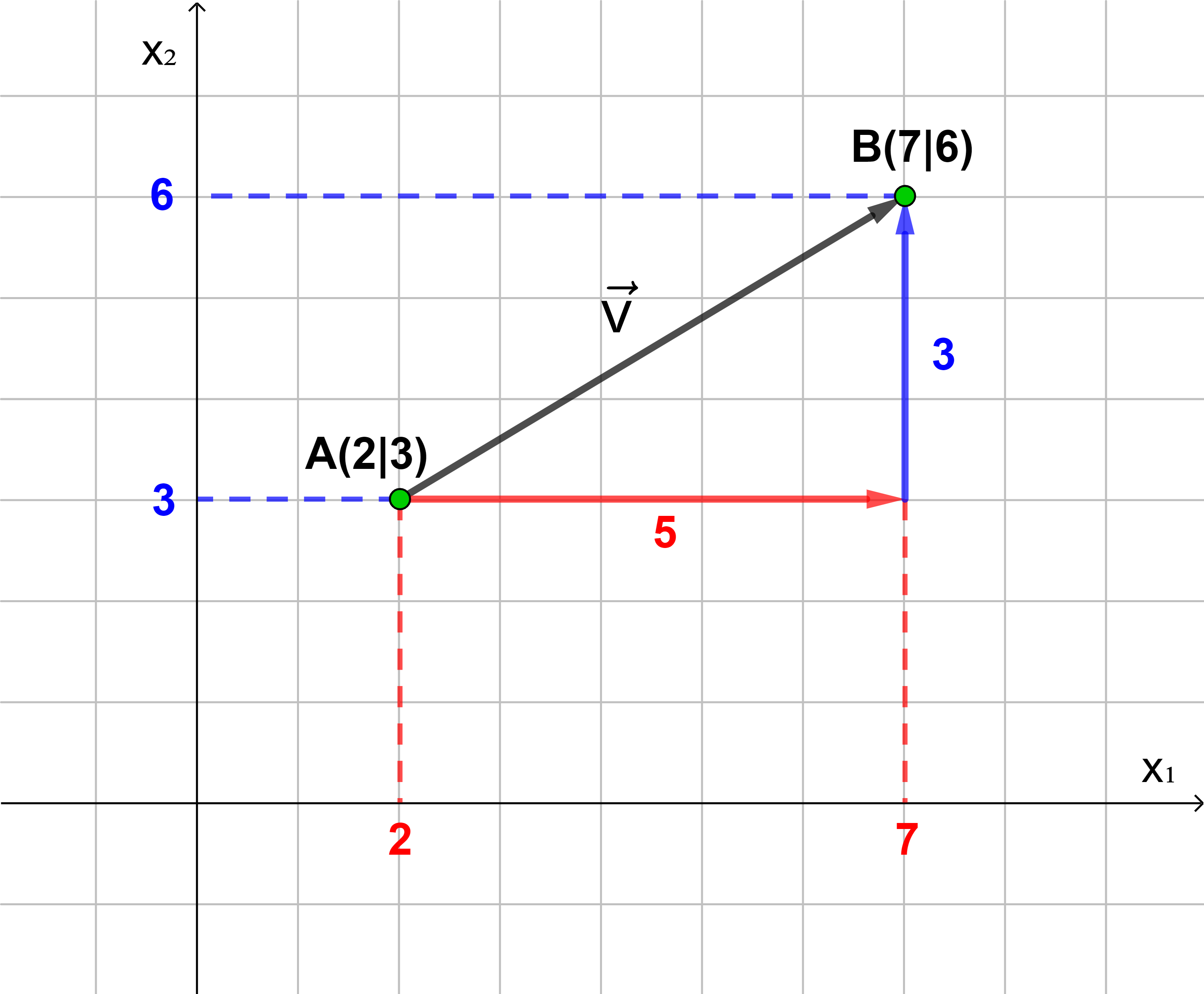
Aus den Koordinaten der Punkte A und B kann man die Koordinaten des Verbindungsvektors berechnen:
→
v
=
(
7 − 2
6 − 3
)
=
(
5
3
)
Bei der Berechnung der Vektorkoordinaten muss die Reihenfolge der Punktkoordinaten beachtet werden. Die Koordinaten des Endpunktes stehen vor dem Minuszeichen, die Koordinaten des Anfangspunktes stehen hinter dem Minuszeichen.
Der Verbindungsvektor der Punkte A(a1|a2) und B(b1|b2) in der Ebene hat die Koordinaten:
⟶
A
B
=
(
b1 − a1
b2 − a2
)
Der Verbindungsvektor der Punkte A(a1|a2|a3) und B(b1|b2|b3) im Raum hat die Koordinaten:
⟶
A
B
=
(
b1 − a1
b2 − a2
b3 − a3
)
Beispiele:
Der Verbindungsvektor der Punkte A(-2 | 5) und B(3 | -4) in der Ebene hat die Koordinaten:
⟶
A
B
=
(
3 − (-2)
-4 − 5
)
=
(
5
-9
)
Der Verbindungsvektor der Punkte P(3 | -1 | 6) und Q(-7 | -2 | 8) im Raum hat die Koordinaten:
⟶
P
Q
=
(
-7 − 3
-2 − (-1)
8 − 6
)
=
(
-10
-1
2
)
Der Verbindungsvektor der Punkte B(3 | -4) und A(-2 | 5) in der Ebene hat die Koordinaten:
⟶
B
A
=
(
-2 − 3
5 − (-4)
)
=
(
-5
9
)
Die Vektoren
⟶
AB
und
⟶
BA
sind Gegenvektoren:
⟶
BA
= −
⟶
AB
Gegenvektoren haben entgegengesetzte Koordinaten.
Übung:
Gegeben sind die Punkte
A(
2
|
-7
)
,
B(
4
|
3
)
,
C(
-6
|
-1
)
und
D(
8
|
5
)
.
Berechnen Sie die Koordinaten des angegebenen Vektors.
⟶
A
B
=
(
−
−
)
=
(
)
Gegeben sind die Punkte
P(
1
|
-8
|
-3
)
,
Q(
-2
|
5
|
-4
)
,
R(
6
|
7
|
-9
)
und
S(
-3
|
-4
|
3
)
.
Berechnen Sie die Koordinaten des angegebenen Vektors.
⟶
P
Q
=
(
−
−
−
)
=
(
)