3. Rechnen mit Vektoren
← Kapitelübersicht3.1. Addition von Vektoren
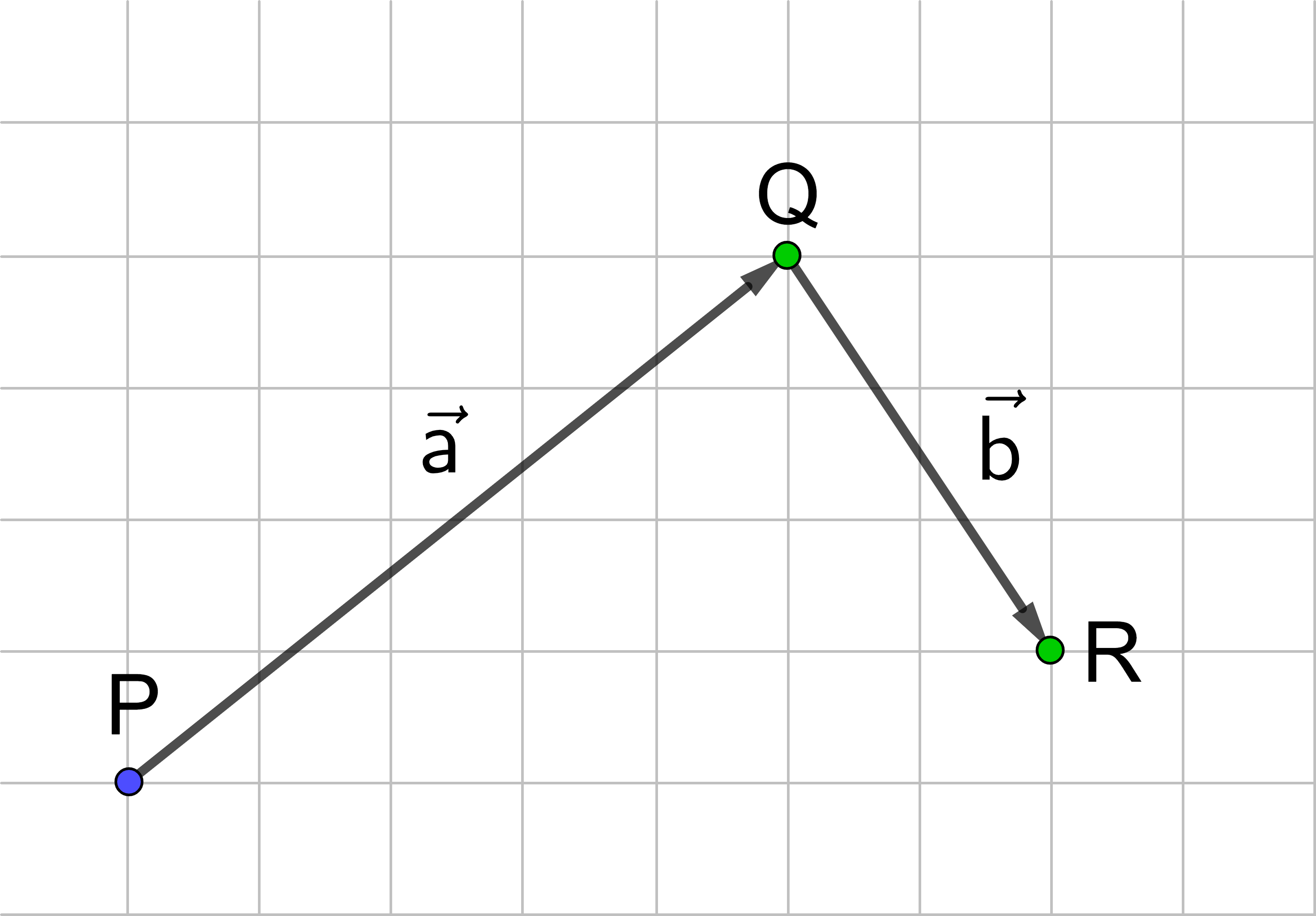
Der blaue Punkt, der auf P liegt, soll durch den Vektor
→
a
von P nach Q verschoben werden, anschließend
durch den Vektor
→
b
von Q nach R.
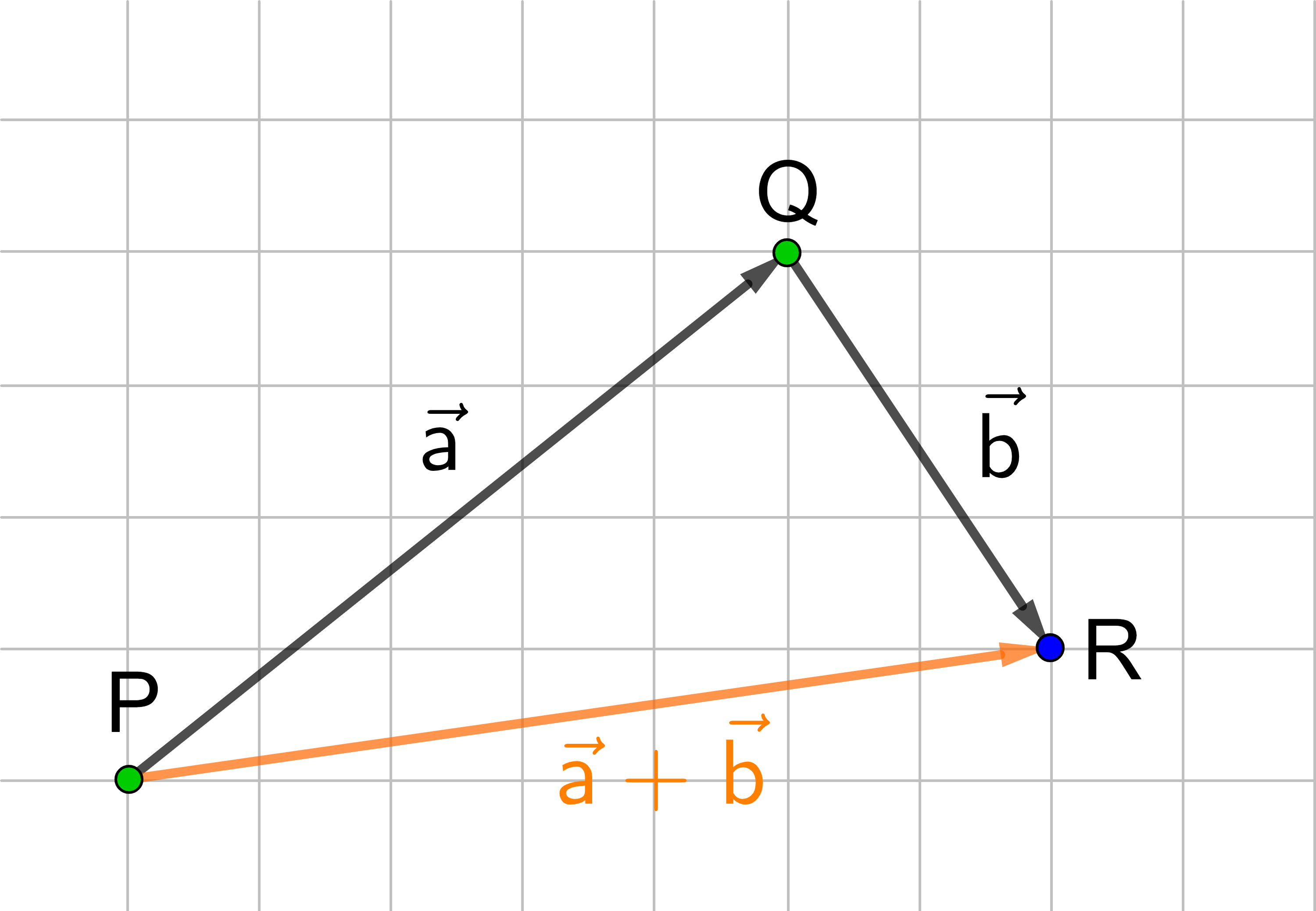
Der blaue Punkt ist durch die Hintereinanderausführung
der Vektoren
→
a
und
→
b
von P nach R gewandert.
Man kann den blauen Punkt auch direkt (ohne Umweg über Q) von P nach R verschieben.
Dieser Vektor wird
→
a
+
→
b
genannt.
Es gilt:
→
a
+
→
b
=
⟶
P
Q
+
⟶
Q
R
=
⟶
P
R
Stimmen der Endpunkt des ersten Vektors und der Anfangspunkt des zweiten Vektors überein, kann man das Ergebnis der Vektoraddition mit Hilfe der gegebenen Punkte benennen.
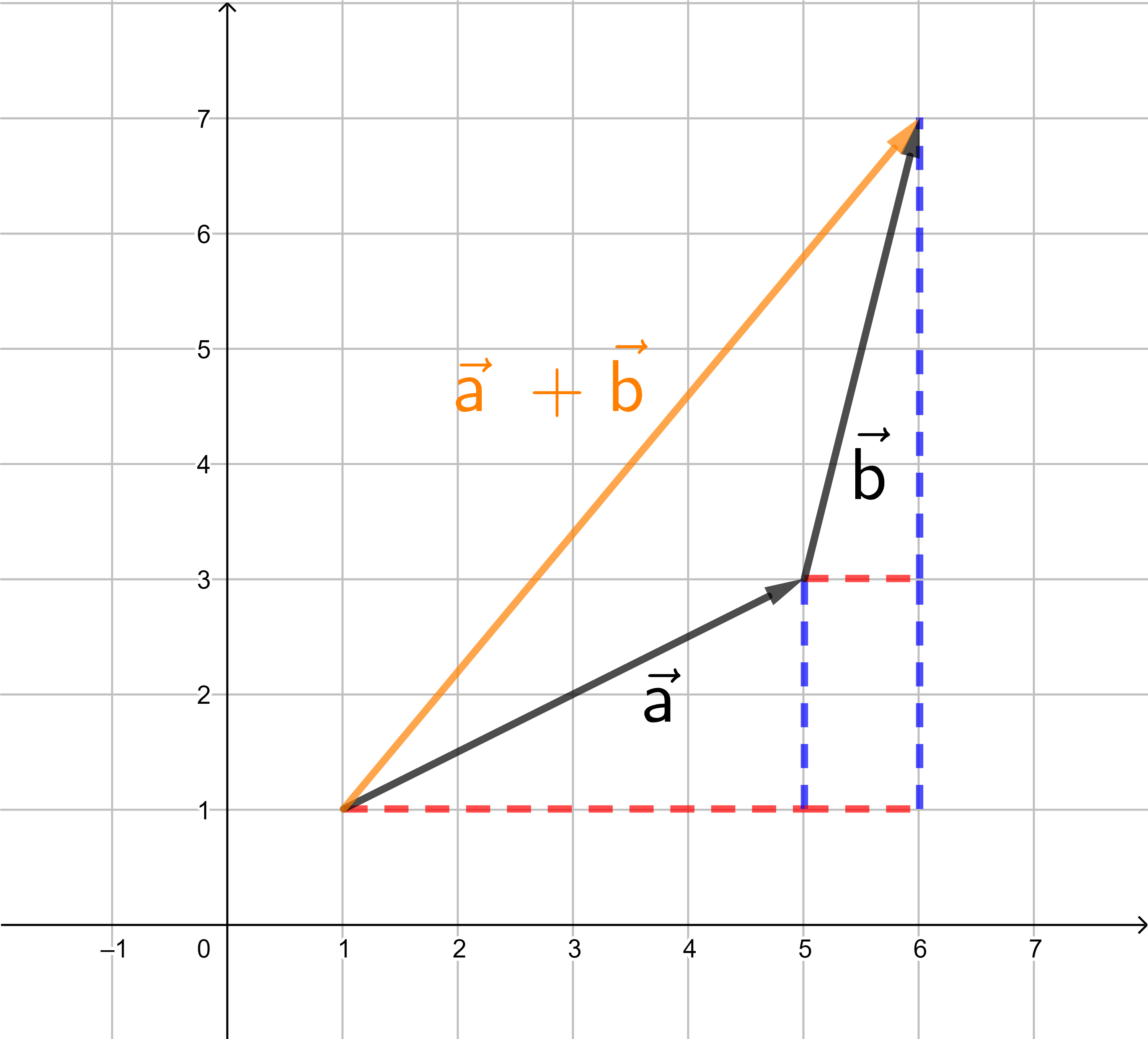
Die Koordinaten des Vektors
→
a
+
→
b
können aus den
Koordinaten der Vektoren
→
a
und
→
b
ermittelt werden.
→
a
+
→
b
=
(
4
2
)
+
(
1
4
)
=
(
4 + 1
2 + 4
)
=
(
5
6
)
Regel für die Berechnung der Koordinaten eines Summenvektors in der Ebene:
→
a
+
→
b
=
(
a1
a2
)
+
(
b1
b2
)
=
(
a1 + b1
a2 + b2
)
Regel für die Berechnung der Koordinaten eines Summenvektors im Raum:
→
a
+
→
b
=
(
a1
a2
a3
)
+
(
b1
b2
b3
)
=
(
a1 + b1
a2 + b2
a3 + b3
)
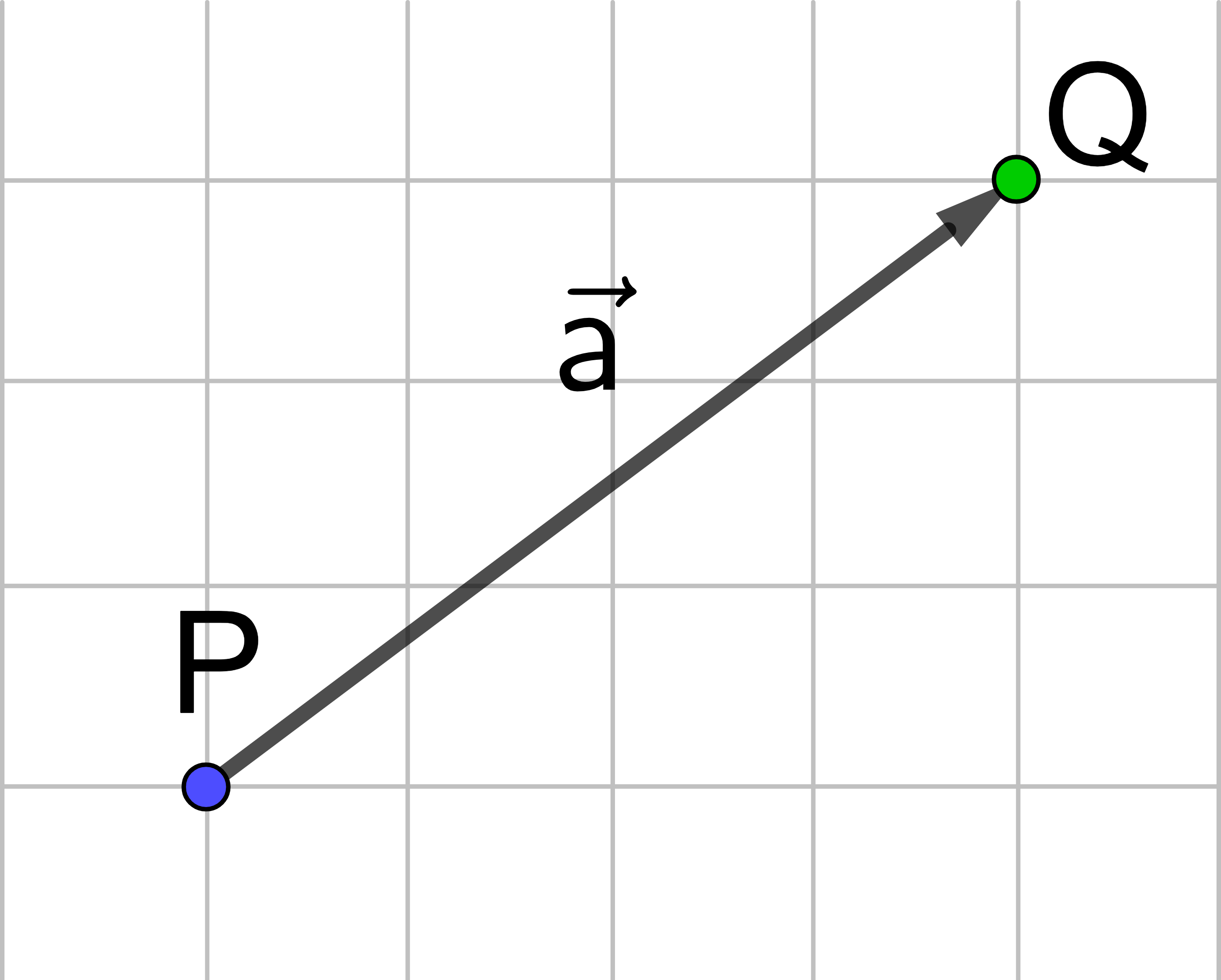
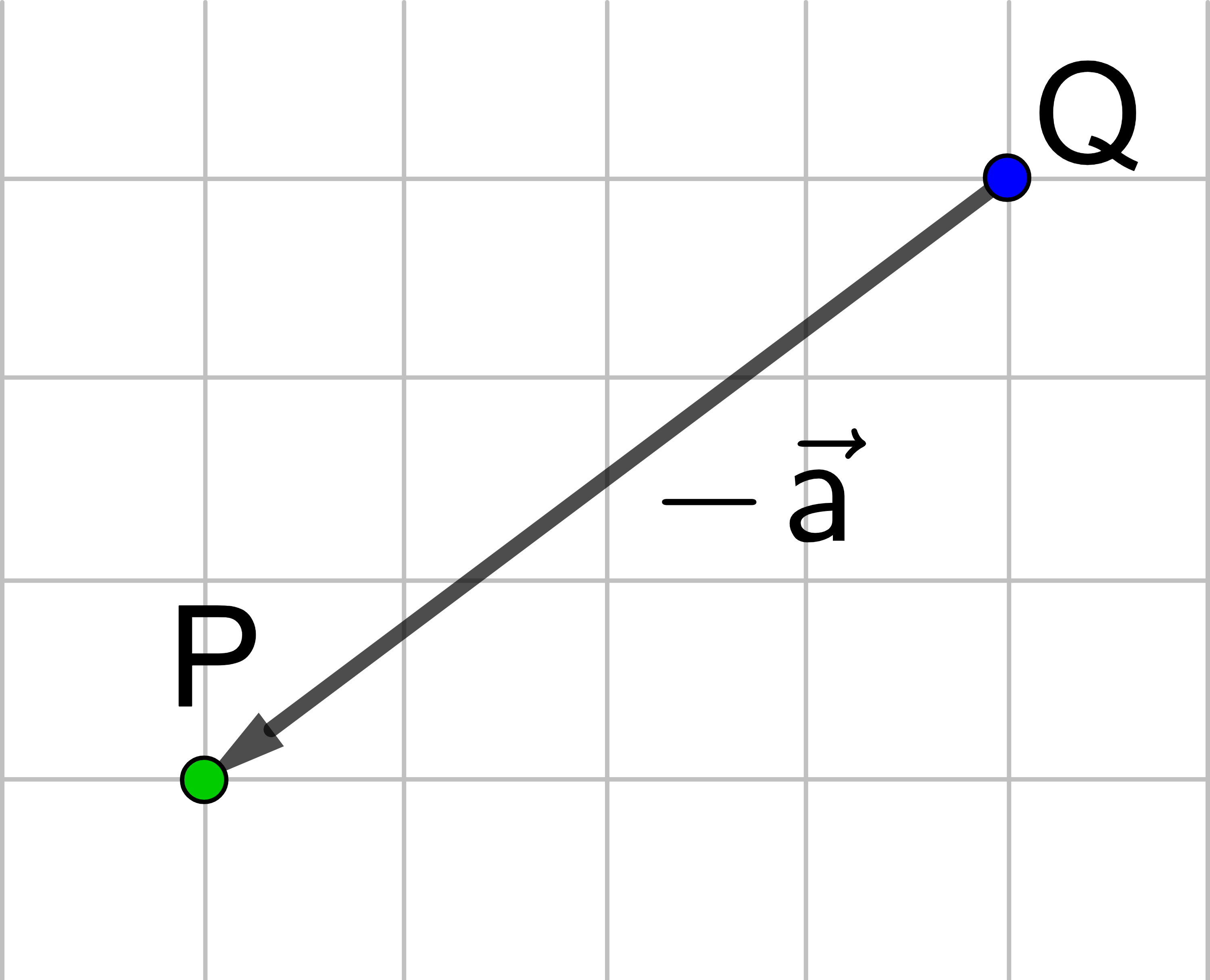
Der blaue Punkt, der auf P liegt, soll durch den Vektor
→
a
von P nach Q verschoben werden, anschließend
durch den Gegenvektor
−
→
a
von Q nach P.
Es gilt:
→
a
+
(−
→
a
)
=
⟶
P
Q
+
⟶
Q
P
=
⟶
P
P
=
→
0
Der blaue Punkt liegt nach der Hintereinanderausführung der beiden Verschiebungen wieder auf seinem Ausgangspunkt P. Er hat seine Position im Endeffekt nicht geändert.
Der Vektor
→
0
wird Nullvektor genannt. Er verändert die Lage eines Punktes nicht.
Alle Koordinaten des Nullvektors sind null.
Übung 1:
Bestimmen Sie die Koordinaten des Vektors
→
a
+
→
b
.
Ziehen Sie dazu den Pfeil des Vektors
→
b
in die richtige Position.
→
a
+
→
b
=
(
)
Übung 2:
⟶
A
B
+
⟶
B
C
Entscheiden Sie, ob das Ergebnis der Vektoraddition mit Hilfe der vorkommenden Punkte bezeichnet werden kann:
Übung 3:
(
2
5
)
+
(
-4
7
)
=
(
)
(
1
-4
3
)
+
(
-2
5
7
)
=
(
)
Tragen Sie die Koordinaten des Summenvektors in die dafür vorgesehenen Felder ein.
Übung 4:
Gegeben sind die Punkte
A(
3
|
-8
)
,
B(
1
|
5
)
,
C(
-7
|
-2
)
und
D(
9
|
4
)
.
Ermitteln Sie die Koordinaten der angegebenen Verbindungsvektoren und tragen Sie sie in die dafür vorgesehenen Felder ein. Berechnen Sie dann die Koordinaten des Summenvektors und füllen Sie die Eingabefelder in der letzten Vektorklammer aus.
⟶
A
B
+
⟶
C
D
=
(
)
+
(
)
=
(
)
Verbindungsvektoren
Summenvektor