3. Rechnen mit Vektoren

← Kapitelübersicht
3.2.  Subtraktion zweier Vektoren
Die Subtraktion einer reellen Zahl kann man als Addition der Gegenzahl darstellen: 5 - 2 = 5 + (-2).
Die Subtraktion eines Vektors wird in ähnlicher Weise definiert.
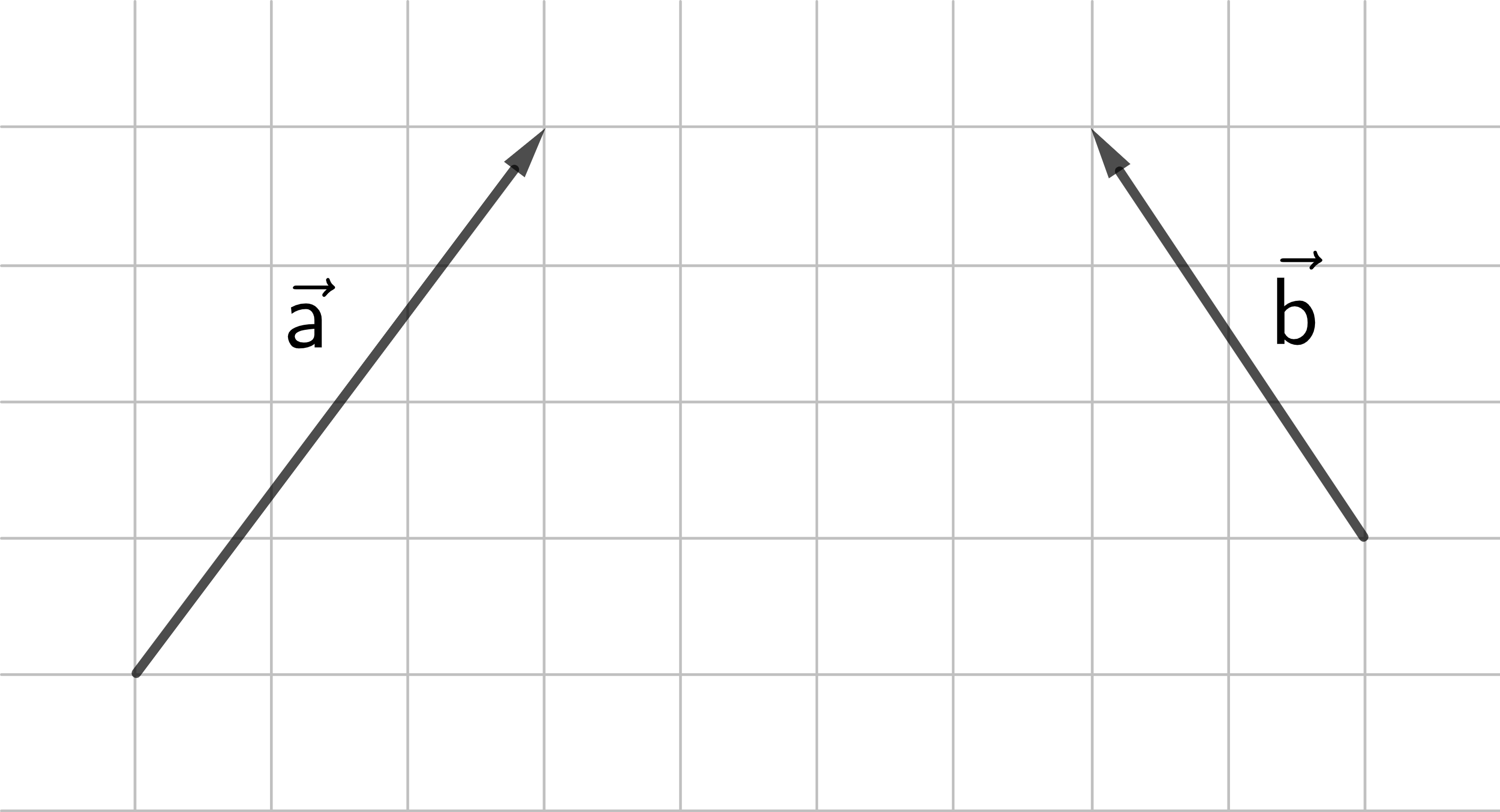
Gegeben sind die Vektoren
→
a
und
→
b
.


Was ist
→
a
 − 
→
b
?
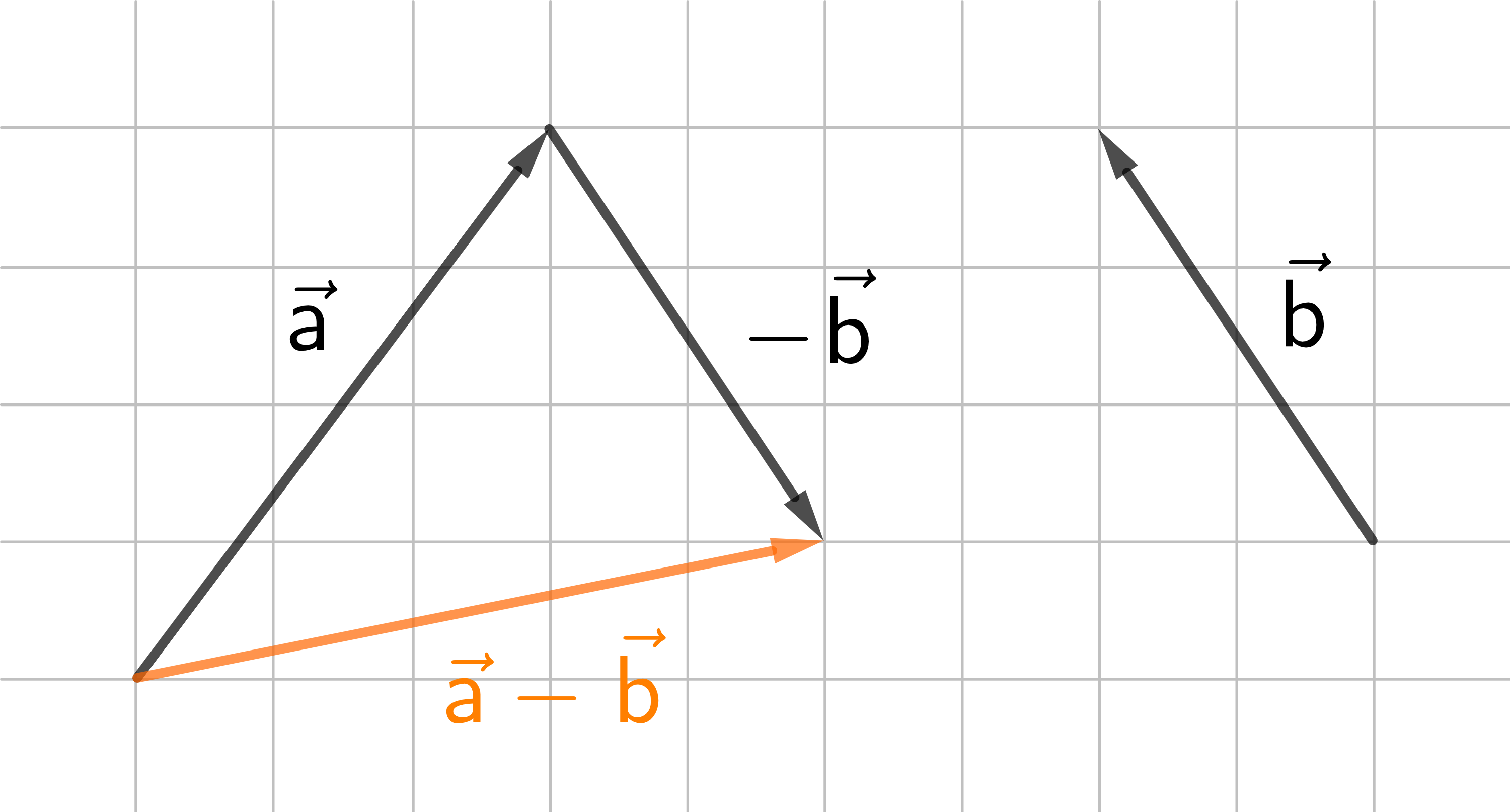
Man subtrahiert einen Vektor, indem man seinen Gegenvektor addiert.
→
a
−
→
b
 = 
→
a
 + ( −
→
b
)
Ein Vektor und sein Gegenvektor haben entgegengesetzte Koordinaten. Deshalb gilt:
→
 a 
−
→
 b 
=
(
a1
a2
)
−
(
b1
b2
)
=
(
a1
a2
)
+
(
−b1
−b2
)
=
(
a1  +  (−b1)
a2  +  (−b2)
)
=
(
a1  −  b1
a2  −  b2
)
Beispiel:
(
5
-3
)
−
(
7
-8
)
=
(
 5   −    7 
 -3   −  (-8)
)
=
(
-2
5
)
Der Vektor
⟶
BC
ist Gegenvektor von
⟶
CB
. Deshalb gilt:
⟶
A
B
−
⟶
C
B
=
⟶
A
B
+
⟶
B
C
=
⟶
A
C
Übung 1:
Klicken Sie auf die richtige Antwort. Der orangefarbene Pfeil repräsentiert den Vektor
Kontrolle
Lösung
Neue Aufgabe
Übung 2:
Entscheiden Sie: Kann das Ergebnis des folgenden Vektorterms als Verbindungsvektor zweier vorkommender Punkte dargestellt werden?
⟶
A
B
−
⟶
C
B
Kontrolle
Lösung
Neue Aufgabe
Übung 3:
Tragen Sie die Koordinaten des Ergebnisvektors in die dafür vorgesehenen Felder ein.
(
3
-7
)
−
(
(
2
-5
)
+
(
-4
1
)
)
=
(

)
Kontrolle
Lösung
Neue Aufgabe
3.1. ← → 3.3.