3. Rechnen mit Vektoren

← Kapitelübersicht
3.3.  Multiplikation eines Vektors mit einem Skalar
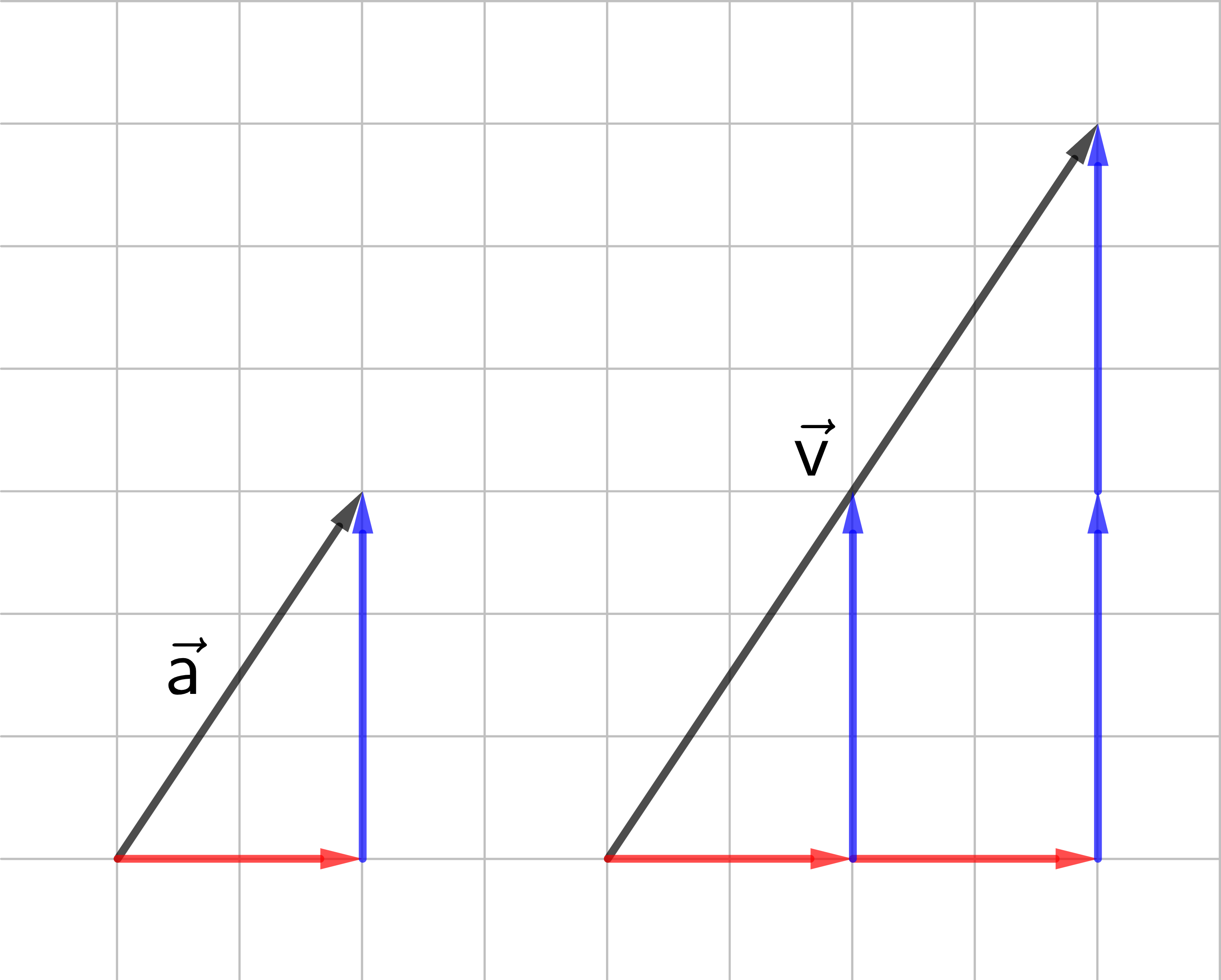
Man kann einen Vektor mit einem Skalar (d. h. einer reellen Zahl) multiplizieren. Das Ergebnis ist wieder ein Vektor. Dieses Kapitel erklärt, wie sich der Vektor durch die Multiplikation verändert.
Verdoppelt man die Koordinaten des Vektors


→
a
=
(
2
3
)
, erhält man den Vektor
→
v
=
(
4
6
)
.



→
v
hat dieselbe Richtung wie
→
a
und die doppelte Länge.



Man sagt:
→
v
=
2 ⋅
→
a
Wir legen fest:
Für einen Vektor
→
a
in der Ebene und eine
beliebige reelle Zahl r 
soll gelten:
r ⋅
→
a
=
r ⋅
(
a1
a2
)
=
(
r ⋅ a1
r ⋅ a2
)
Für einen Vektor
→
a
im Raum und eine
beliebige reelle Zahl r 
soll gelten:
r ⋅
→
a
=
r ⋅
(
a1
a2
a3
)
=
(
r ⋅ a1
r ⋅ a2
r ⋅ a3
)
Beispiel:
4 ⋅
(
3
-5
)
=
(
4 ⋅   3 
4 ⋅ (-5)
)
=
(
12
-20
)
Beispiel:
7 ⋅
(
-1
8
5
)
=
(
7 ⋅ (-1)
7 ⋅   8 
7 ⋅   5 
)
=
(
 -7
56
35
)
Alle Vielfachen  
r ⋅
→
a
 eines Vektors
→
a
 liegen parallel zum Vektor
→
a
.
Ausnahme:  
0 ⋅
→
a
  = 
→
0
    (Nullvektor)
Der Nullvektor hat die Länge 0. Er kann nicht parallel zum Vektor
→
a
 liegen.
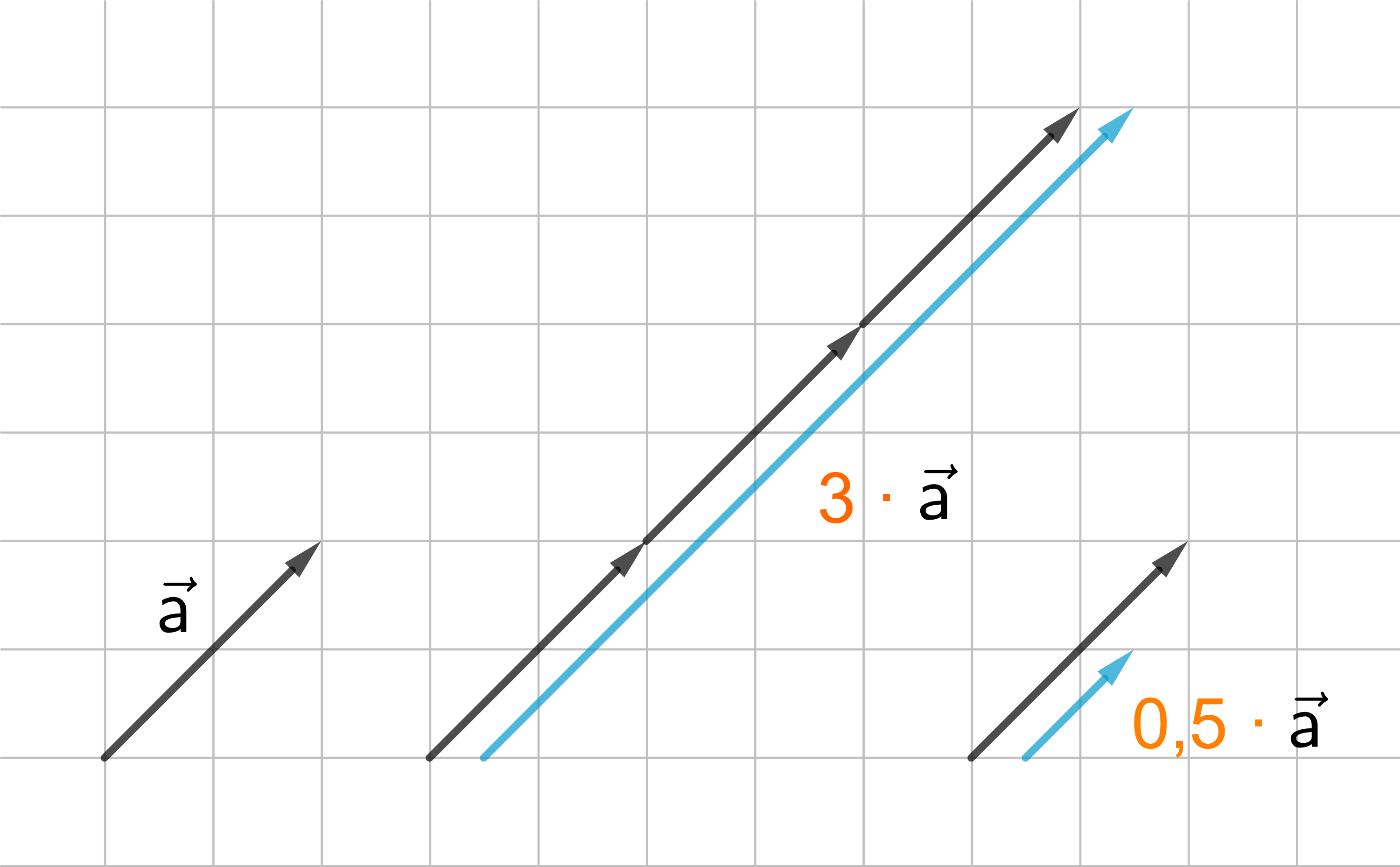
Ist r eine positive Zahl, zeigt der Vektor
→
v
 = 
 r ⋅
→
a

in dieselbe Richtung wie
→
a
.
→
v
 ist r-mal so lang wie
→
a
.
→
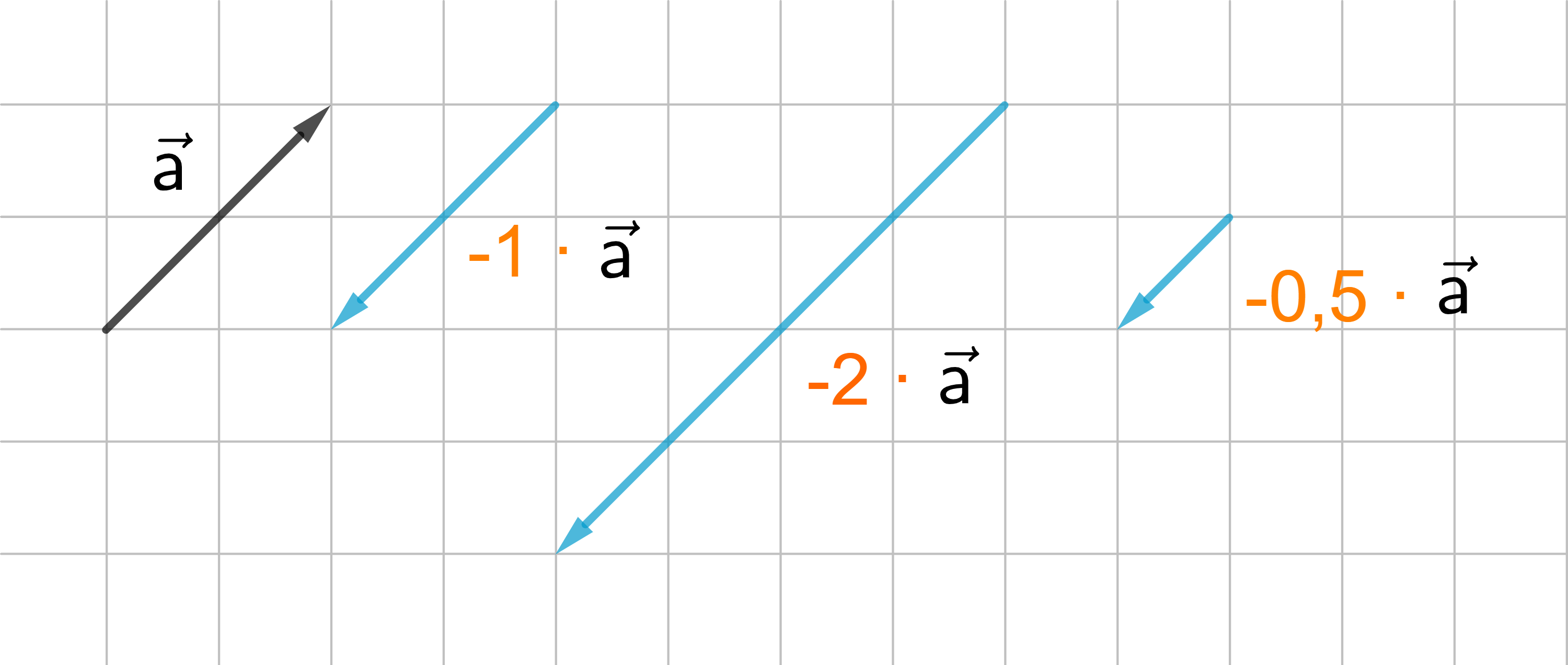
v
 = 
 -1 ⋅
→
a
 =  −
→
a
ist der Gegenvektor von
→
a
.
Ist r eine negative Zahl, zeigt der Vektor
→
v
 = 
 r ⋅
→
a

in die entgegengesetzte Richtung von
→
a
.
Ist ein Vektor ein Vielfaches eines anderen Vektors, nennt man die beiden Vektoren linear abhängig oder kollinear.
Summen aus Vielfachen mehrerer Vektoren werden Linearkombinationen genannt.
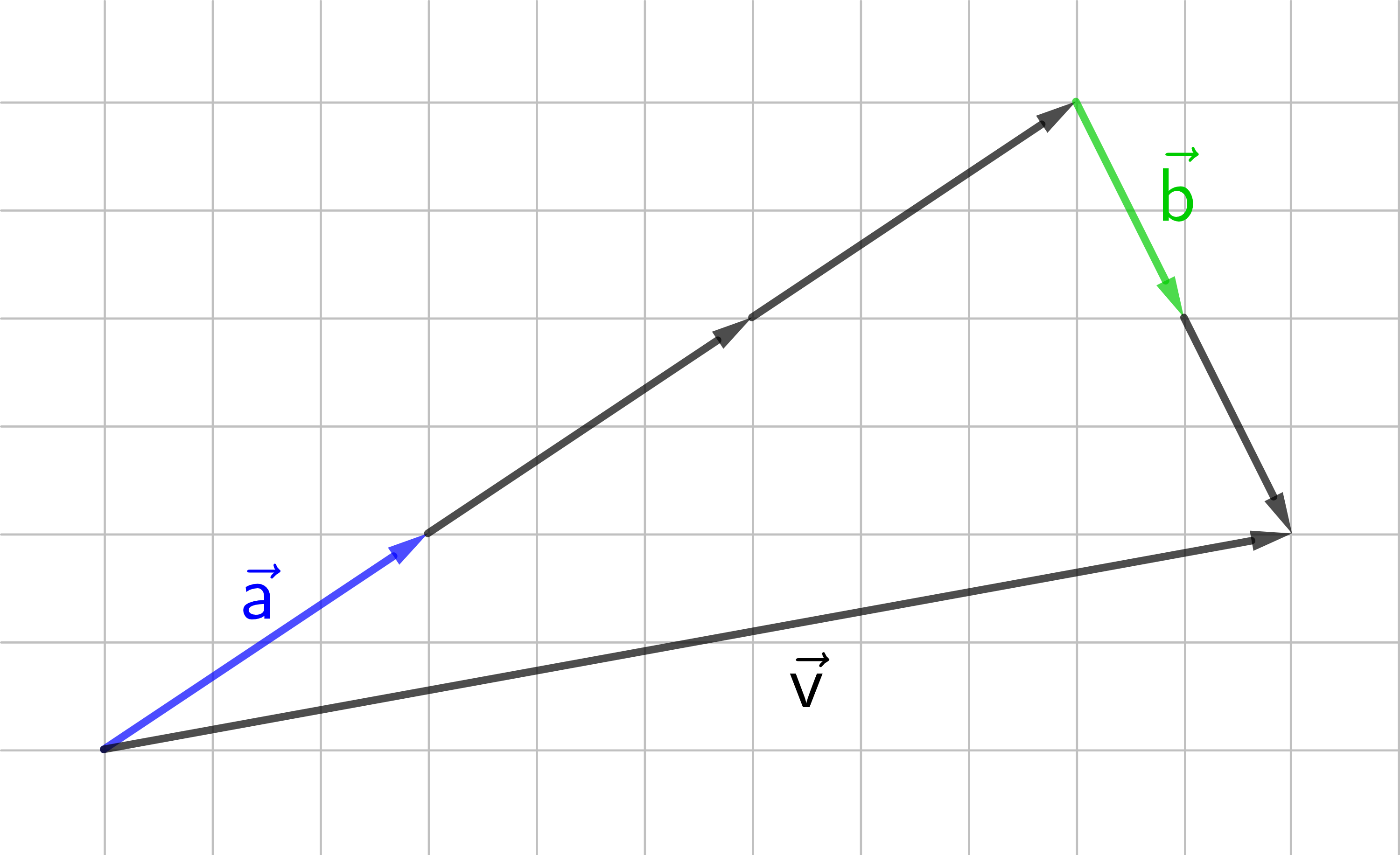
Der Vektor
→
v
ist das Ergebnis einer Linearkombination

der Vektoren
→
a
und
→
b
.
→
v
=
 3 ⋅
→
a
+
 2 ⋅
→
b
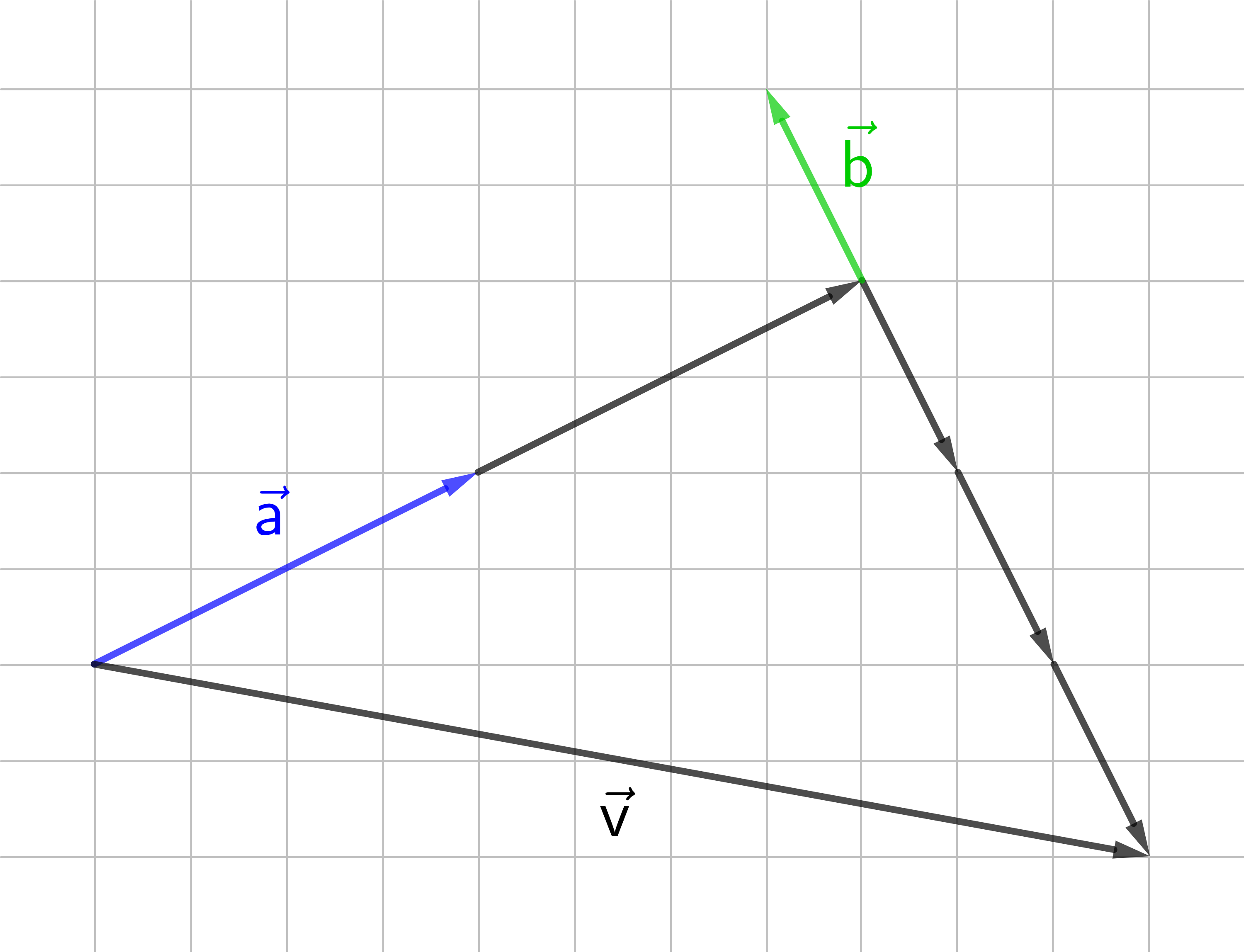
Auch in diesem Beispiel ist der Vektor
→
v
das Ergebnis

einer Linearkombination der Vektoren
→
a
und
→
b
.
→
v
=
 2 ⋅
→
a
+
 (-3) ⋅
→
b
=
 2 ⋅
→
a
−
 3 ⋅
→
b
Übung 1:
Entscheiden Sie:

Ist der Vektor
→
v
ein Vielfaches des Vektors
→
a
?
Kontrolle
Hilfe
Lösung
Neue Aufgabe
Übung 2:
Entscheiden Sie:

Ist der Vektor
→
v
ein Vielfaches des Vektors
→
a
?
→
v
=
(
12
-28
)
→
a
=
(
3
-7
)
Kontrolle
Lösung
Neue Aufgabe
Übung 3:
Berechnen Sie die Koordinaten des Ergebnisvektors der folgenden Linearkombination.
4
 ⋅
(
2
-7
)
+
3
 ⋅
(
1
5
)
=
(

)
Kontrolle
Lösung
Neue Aufgabe
Übung 4:
In der Zeichnung repräsentiert der blaue Pfeil

den Vektor
→
a
, der grüne Pfeil den Vektor
→
b

und der orangefarbene Pfeil den Vektor
→
v
.
Stellen Sie den Vektor
→
v
als Linearkombination

der Vektoren
→
a
und
→
b
dar.
→
v
=
⋅
→
a
+
⋅
→
b
Kontrolle
Hilfe
Lösung
Neue Aufgabe
3.2. ← → 3.4.