3. Rechnen mit Vektoren
← Kapitelübersicht3.4. Gesetze für das Rechnen mit Vektoren
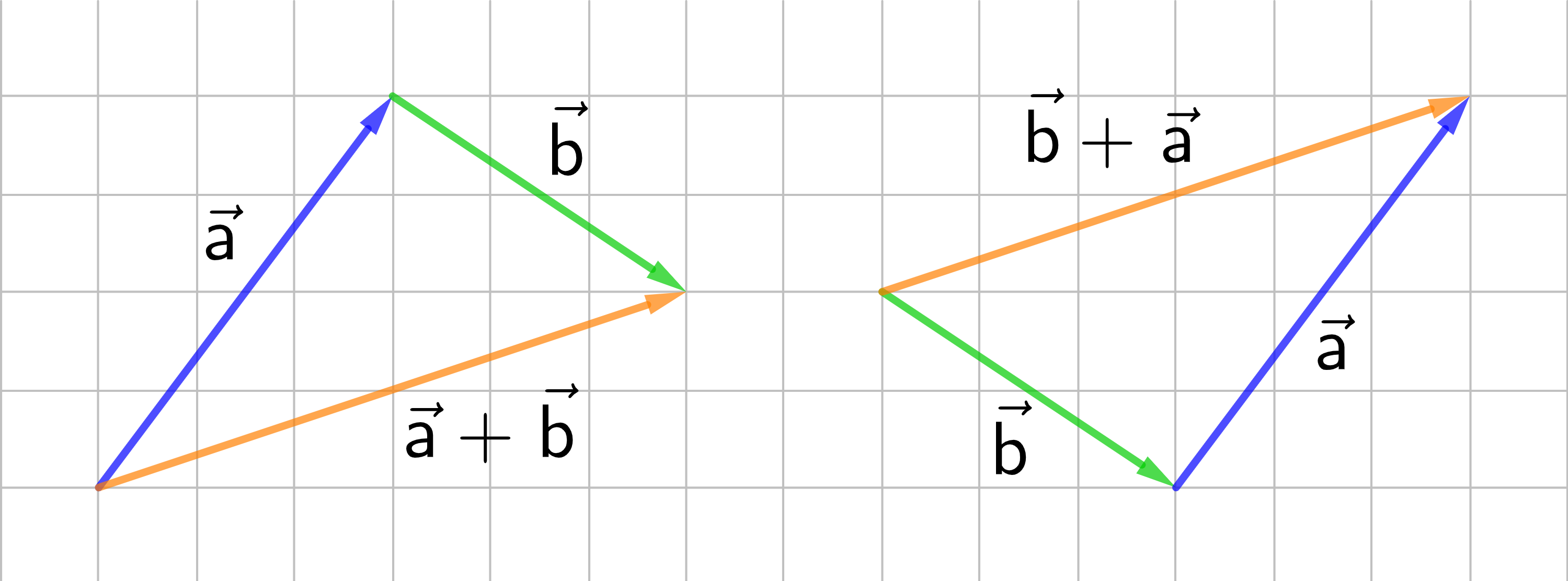
Für die Addition von Vektoren gilt das Kommutativgesetz:
→
a
+
→
b
=
→
b
+
→
a
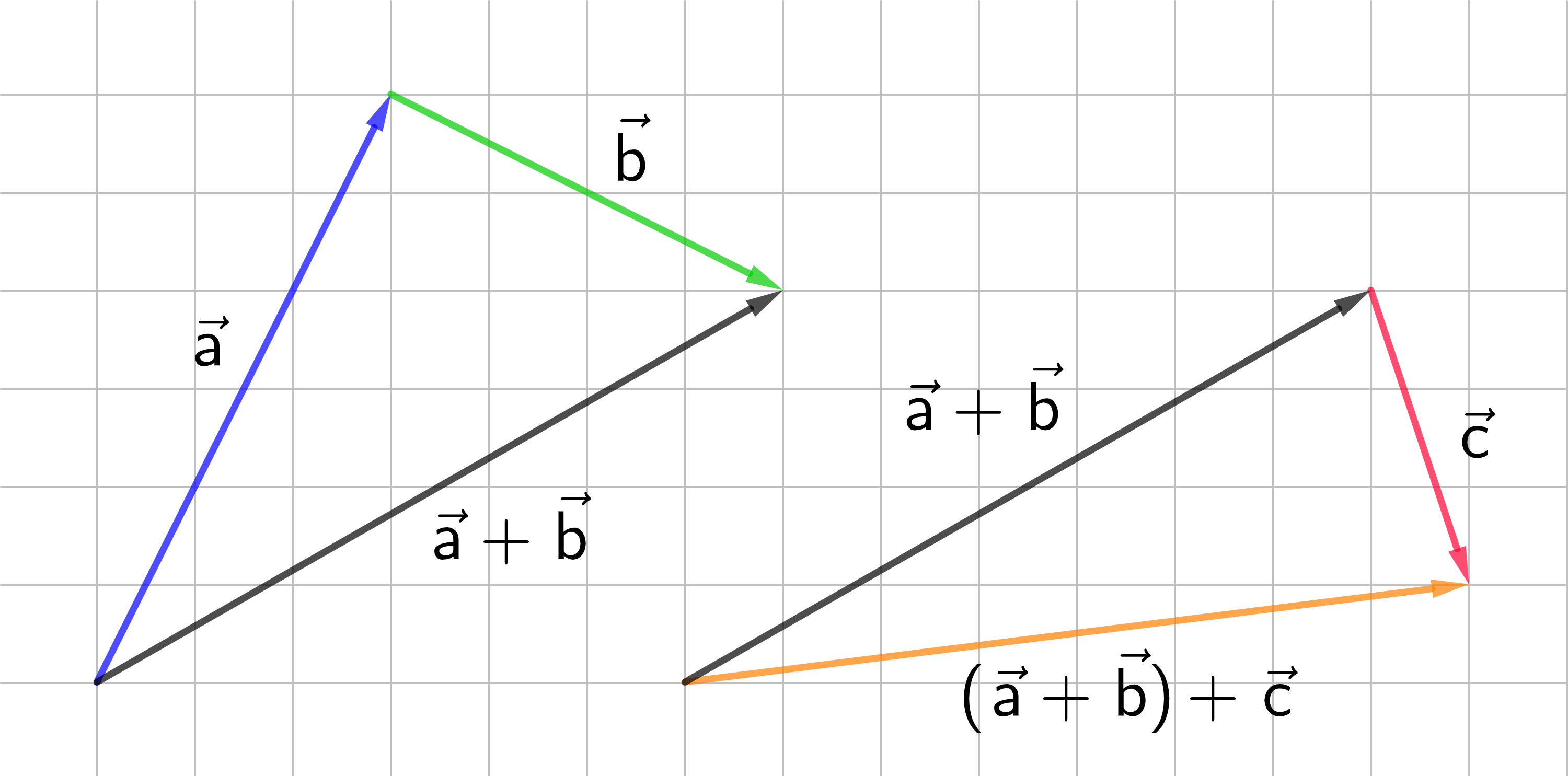
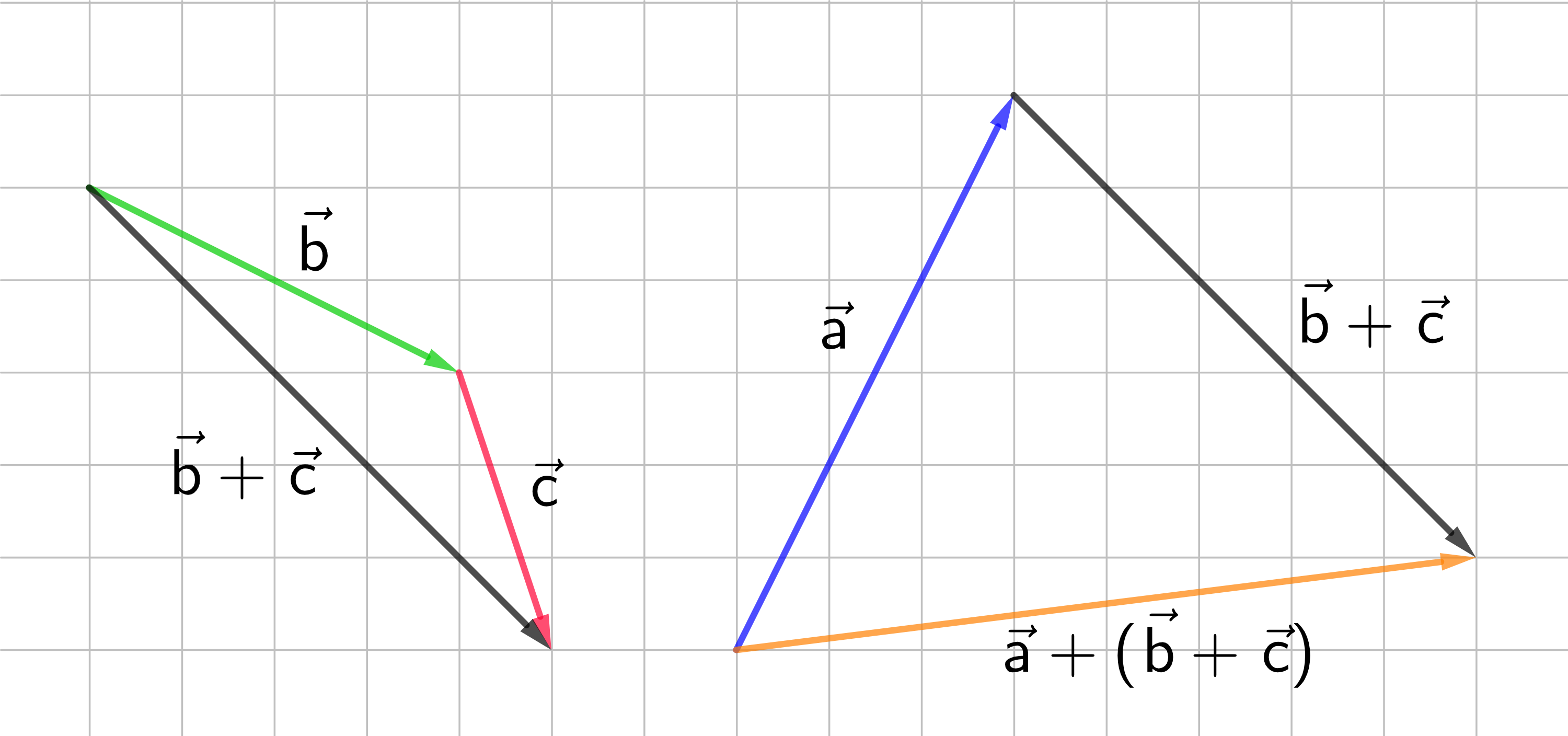
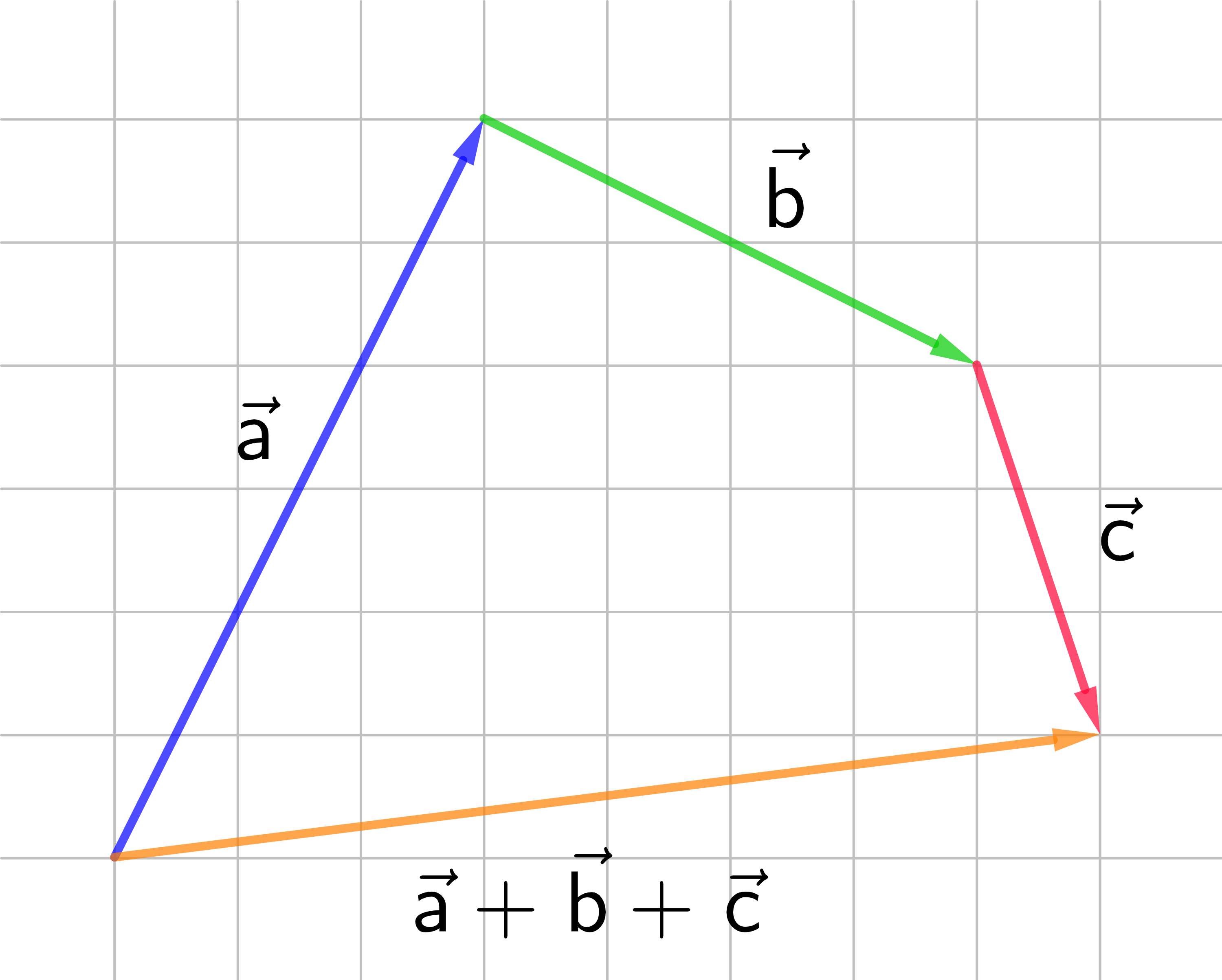
Für die Addition von Vektoren gilt das Assoziativgesetz:
(
→
a
+
→
b
)
+
→
c
=
→
a
+
(
→
b
+
→
c
)
=
→
a
+
→
b
+
→
c
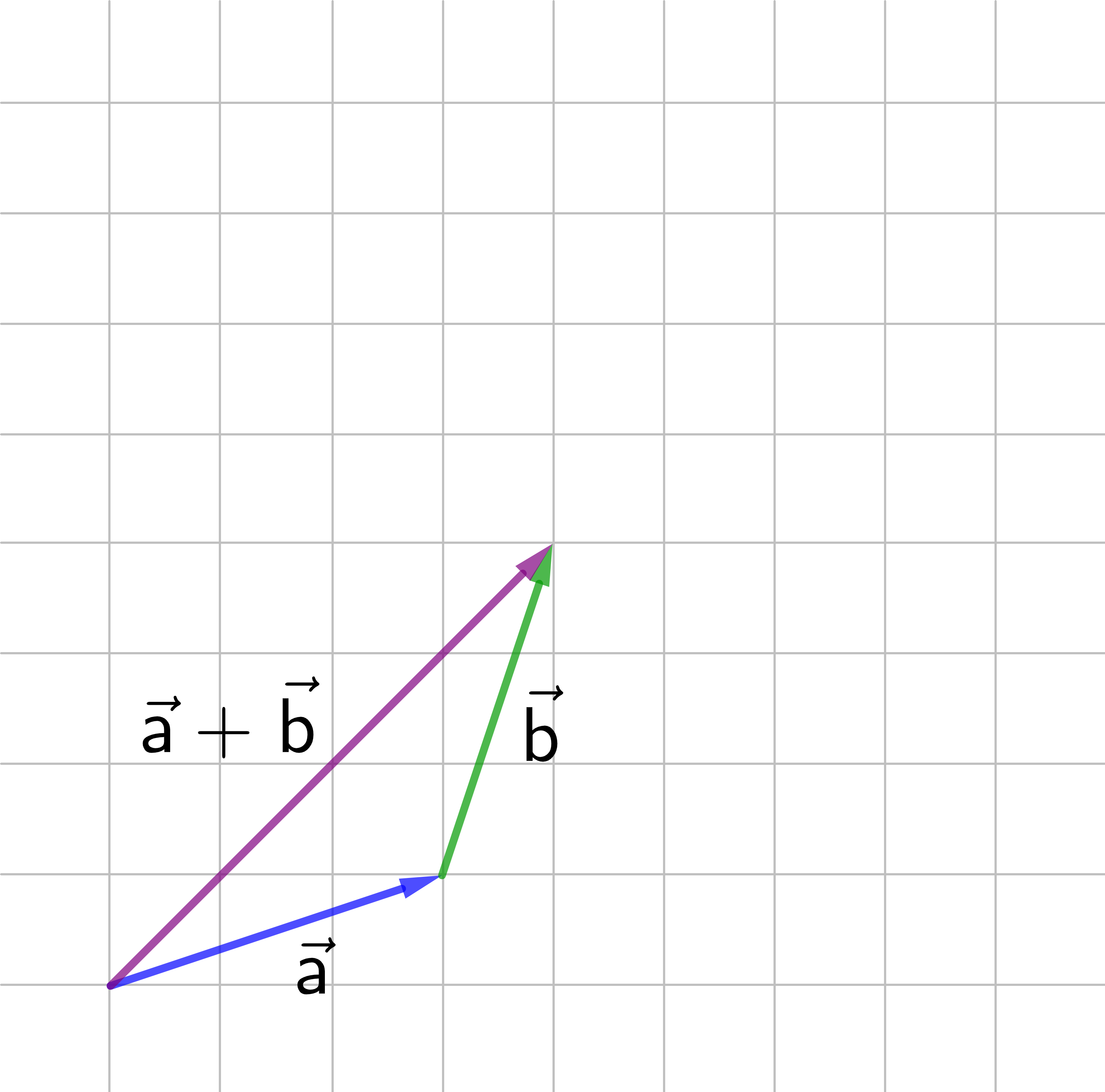
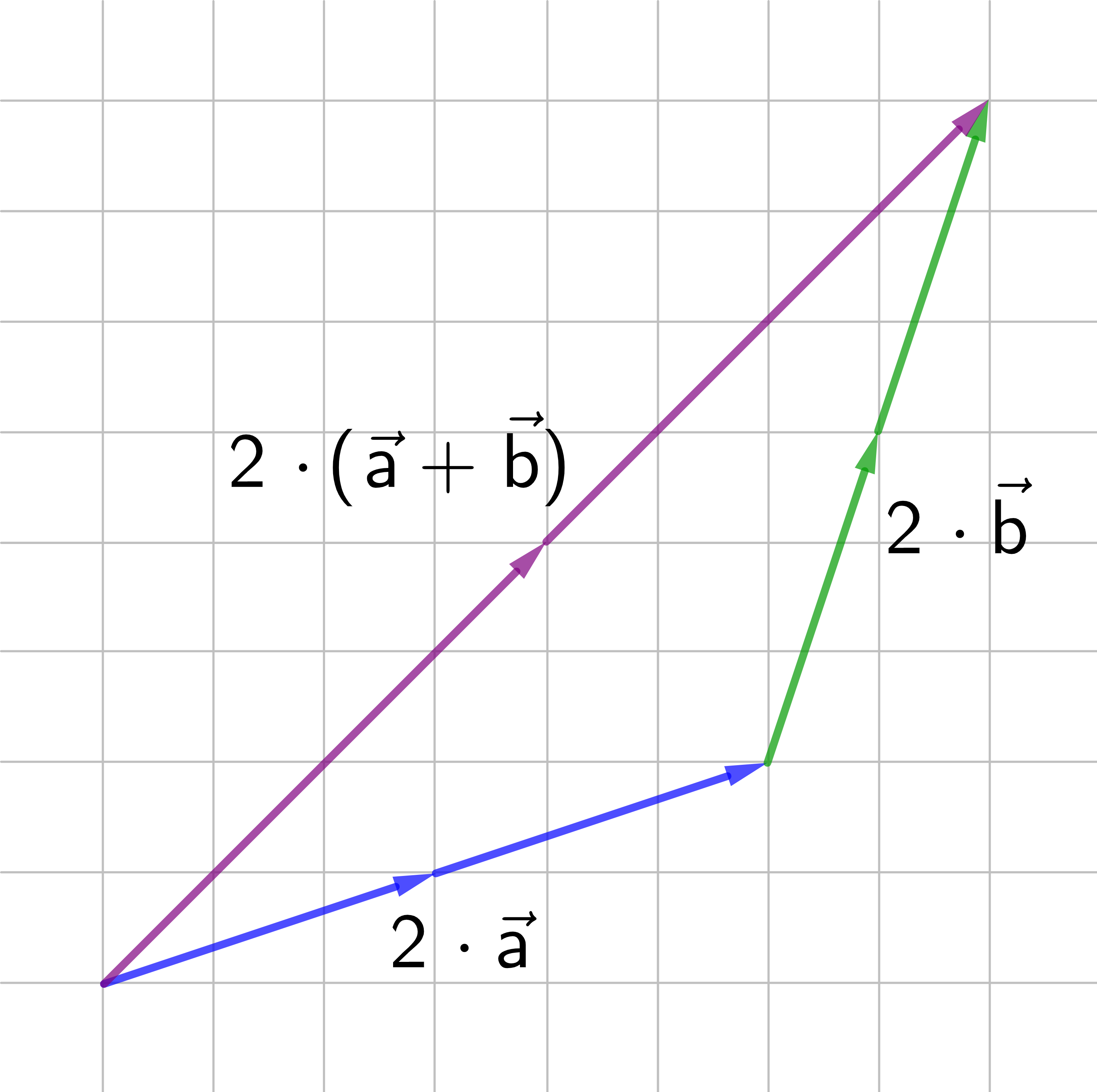
Für die Addition von Vektoren und die Multiplikation mit einem Skalar gelten zwei Distributivgesetze.
Die Zeichnungen veranschaulichen:
2 ⋅
→
a
+
2 ⋅
→
b
=
2 ⋅
(
→
a
+
→
b
)
Allgemein gilt für jede beliebige reelle Zahl r :
r ⋅
→
a
+
r ⋅
→
b
=
r ⋅
(
→
a
+
→
b
)
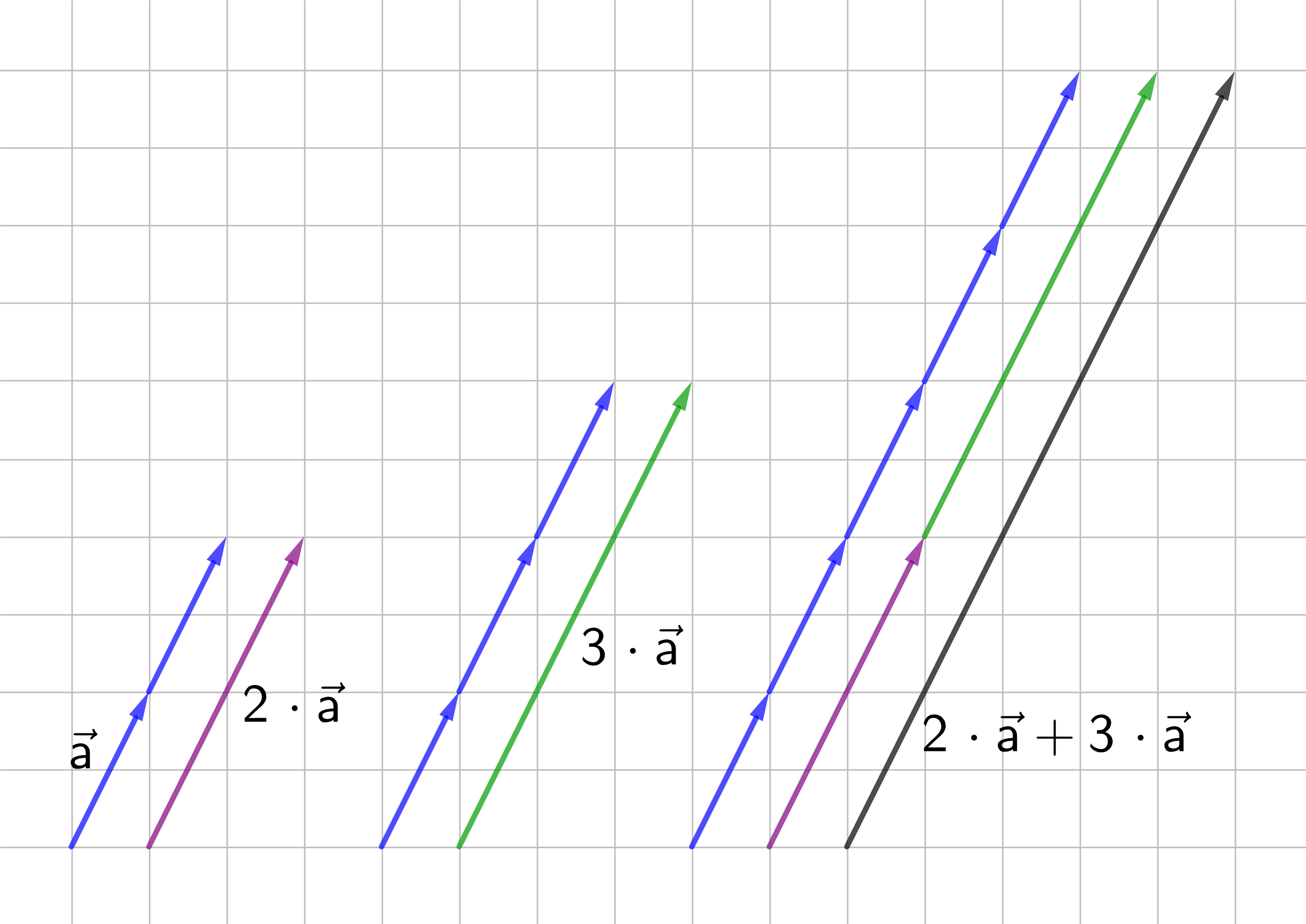
In der Zeichnung ist dargestellt:
2 ⋅
→
a
+
3 ⋅
→
a
=
(2 + 3)
⋅
→
a
=
5 ⋅
→
a
Allgemein gilt für beliebige reelle Zahlen r und s :
r ⋅
→
a
+
s ⋅
→
a
=
(r + s)
⋅
→
a
Übung:
Wenden Sie die Gesetze für das Rechnen mit Vektoren an, um den nachfolgenden Term zu vereinfachen.
⟶
B
C
+
⟶
A
B
=
⟶