4. Bestimmung von Punktkoordinaten mit Hilfe von Ortsvektoren
← Kapitelübersicht4.1. Anfangs- und Endpunkt eines Vektors
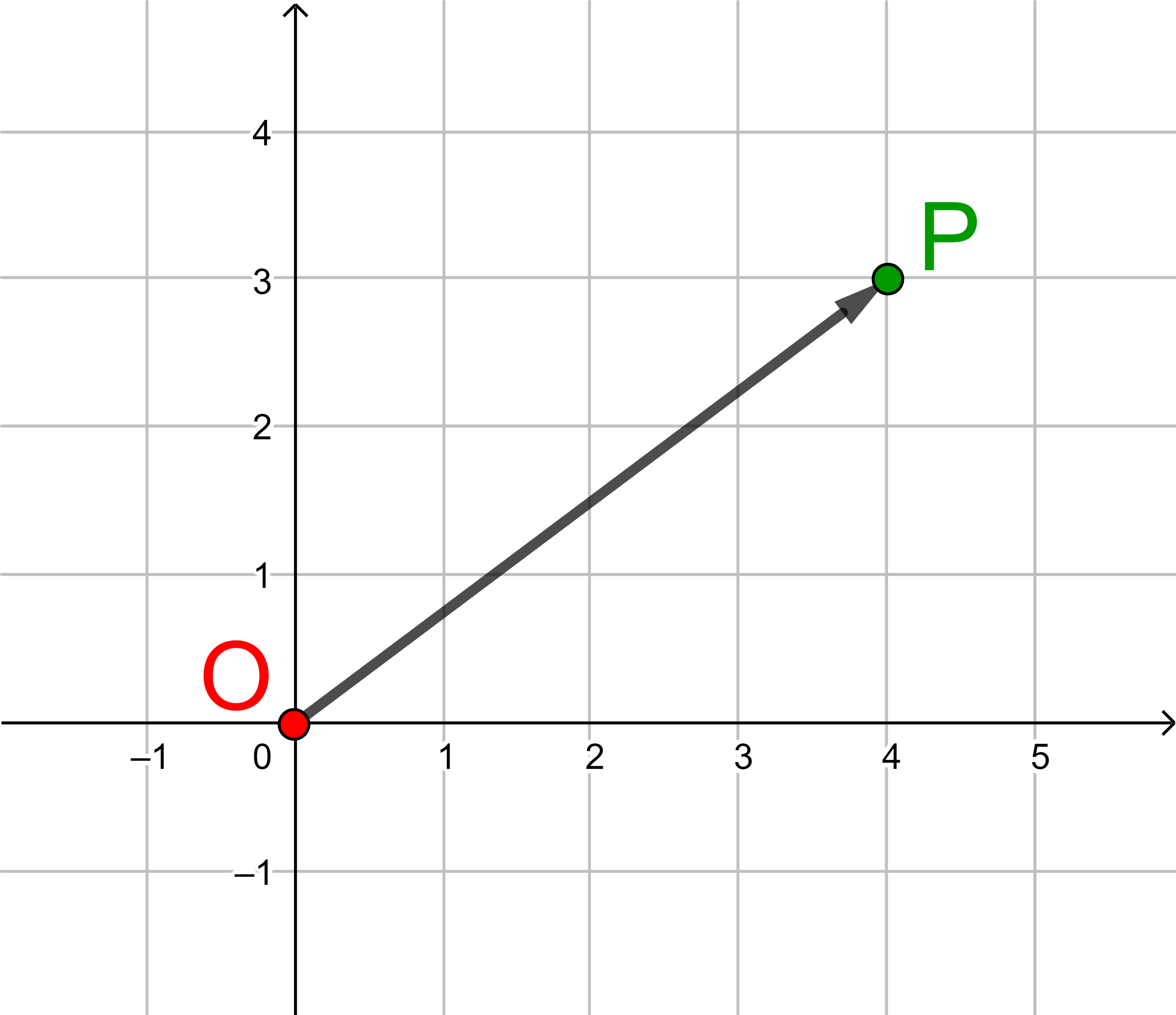
Origo ist das lateinische Wort für "Ursprung". Deshalb wird der Ursprung des Koordinatensystems mit O bezeichnet.
Der Vektor
⟶
OP
=
(
4
3
)
hat die gleichen Koordinaten wie der Punkt P(4 | 3).
Achtung: Vektorkoordinaten schreibt man untereinander, Punktkoordinaten nebeneinander.
Er heißt Ortsvektor zum Punkt P.
Möchte man die Koordinaten eines bestimmten Punktes in der Ebene oder im Raum ermitteln, berechnet man die Koordinaten des Ortsvektors zu diesem Punkt mit Hilfe der Addition oder Subtraktion geeigneter Vektoren.
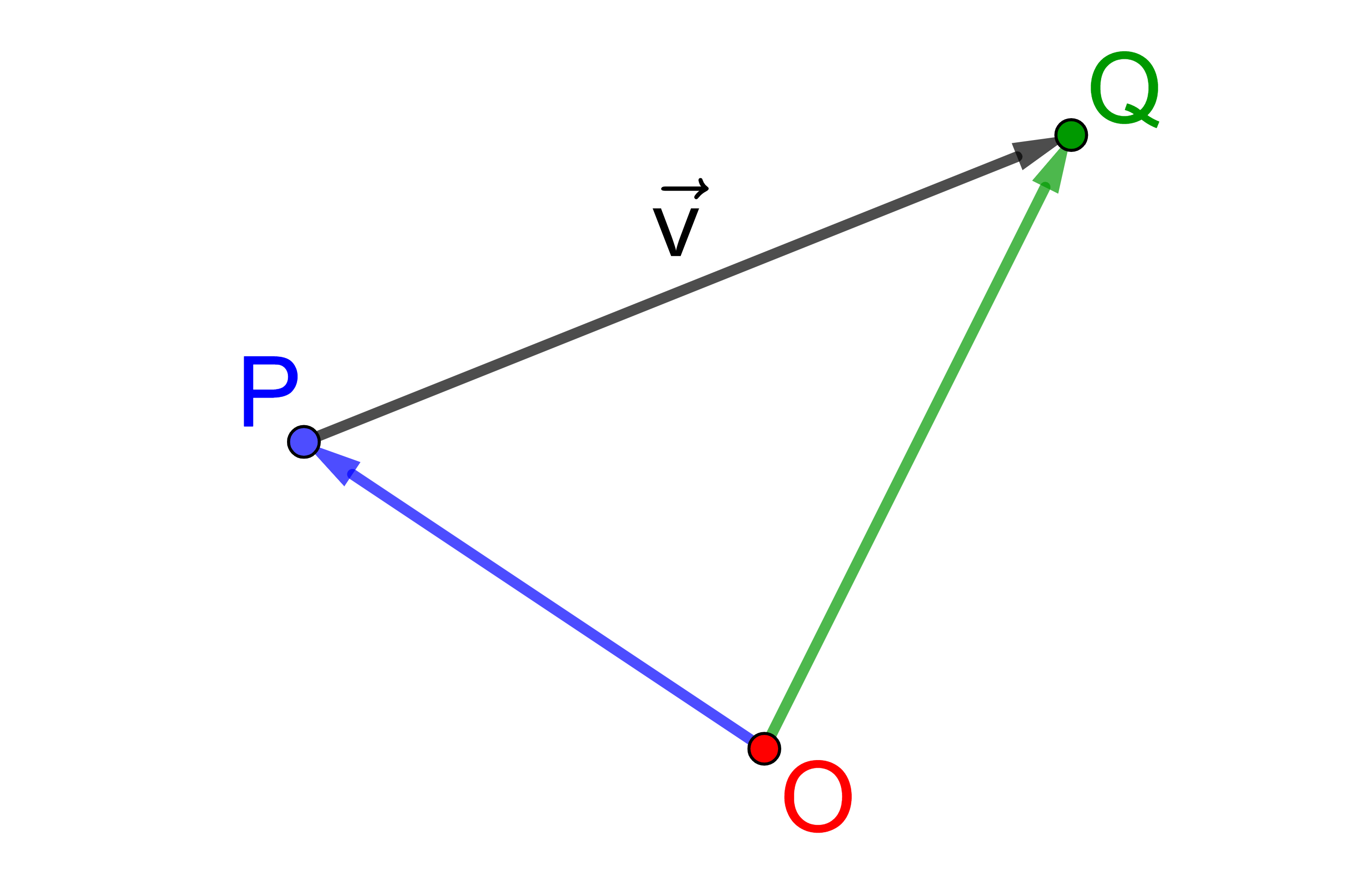
Sind die Koordinaten eines Vektors
→
v
bekannt und die Koordinaten
des Anfangspunktes P gegeben, kann man die Koordinaten des
Endpunktes Q berechnen.
Beispiel:
Gegeben sind P(-3 | 2) und
→
v
=
(
5
2
)
⟶
OQ
=
⟶
OP
+
→
v
=
(
-3
2
)
+
(
5
2
)
=
(
2
4
)
Q(2 | 4) ist der Endpunkt des gegebenen Vektors.
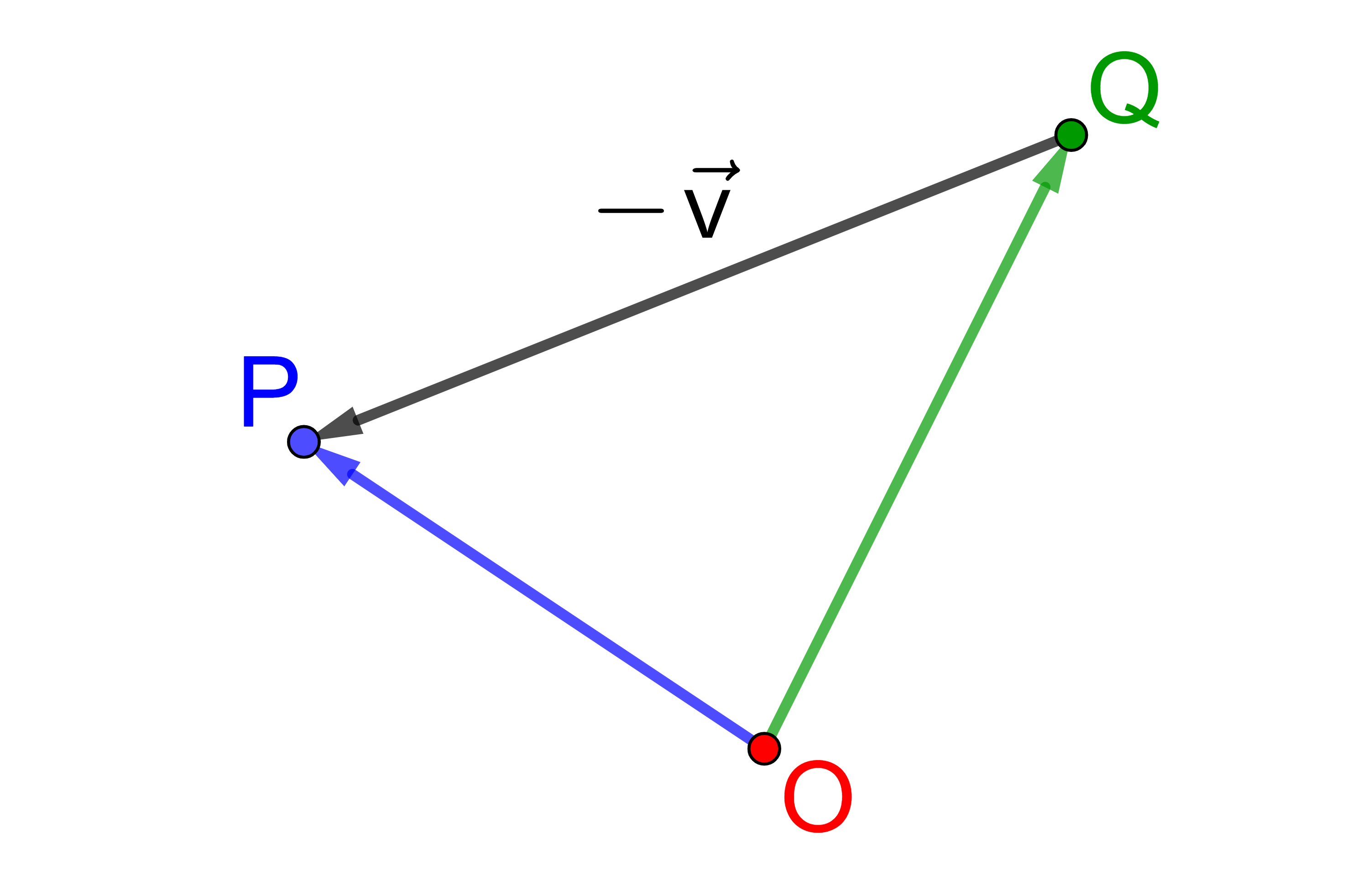
Sind die Koordinaten eines Vektors
→
v
bekannt und die Koordinaten
des Endpunktes Q gegeben, kann man die Koordinaten des
Anfangspunktes P berechnen.
Beispiel:
Gegeben sind Q(2 | 4) und
→
v
=
(
5
2
)
⟶
OP
=
⟶
OQ
+ ( -
→
v
) =
⟶
OQ
−
→
v
=
(
2
4
)
−
(
5
2
)
=
(
-3
2
)
P(-3 | 2) ist der Anfangspunkt des gegebenen Vektors.
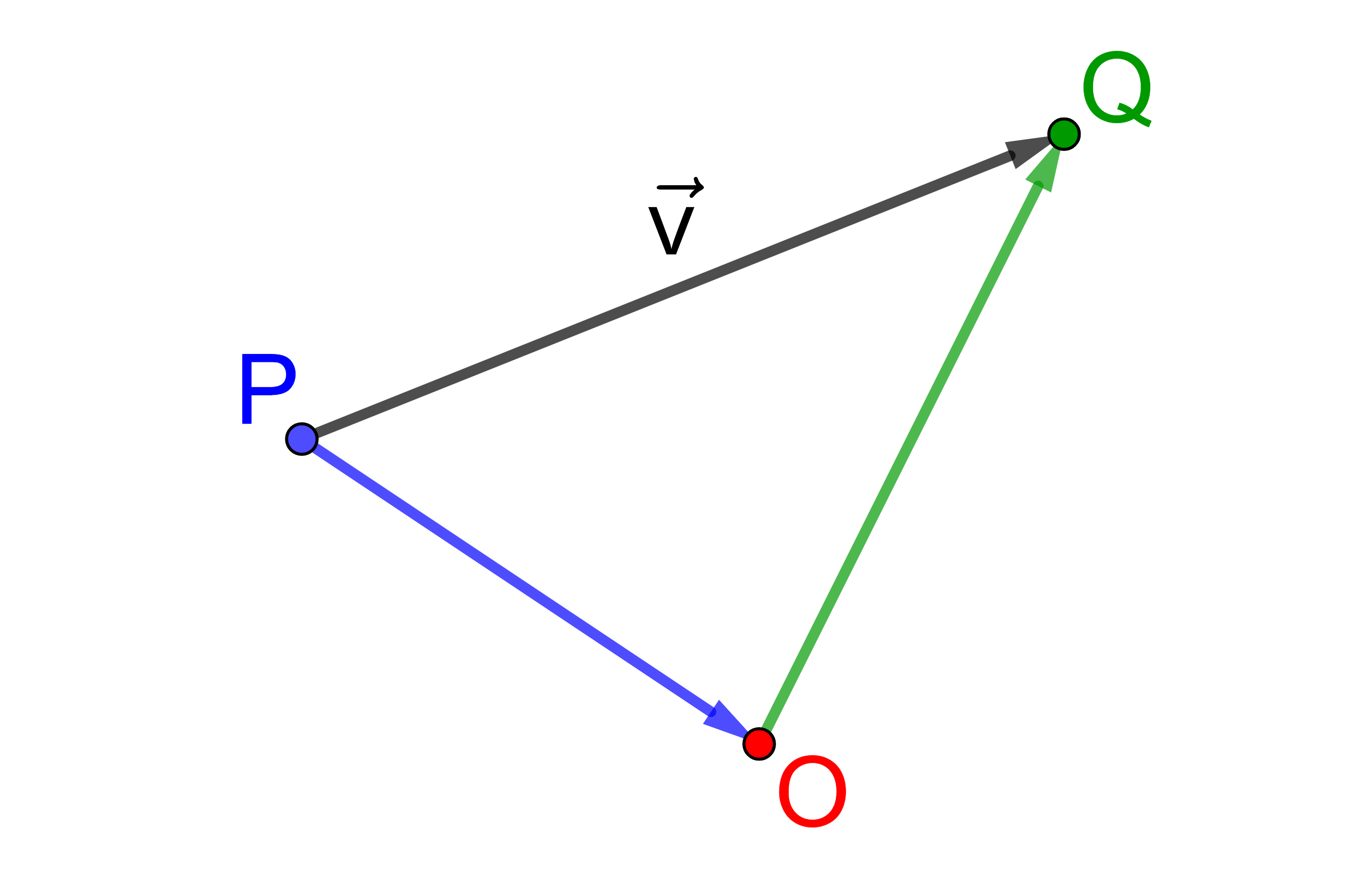
Sind der Anfangspunkt P und der Endpunkt Q eines Vektors
→
v
gegeben, kann man die Koordinaten des Vektors mit Hilfe von
Ortsvektoren berechnen.
Ortsvektoren berechnen.
Beispiel:
Gegeben sind P(-3 | 2) und Q(2 | 4) .
→
v
=
⟶
PQ
=
⟶
PO
+
⟶
OQ
=
⟶
OQ
+
⟶
PO
=
⟶
OQ
−
⟶
OP
(siehe Kapitel 3.2 und 3.4)
⟶
PQ
=
⟶
OQ
−
⟶
OP
=
(
2
4
)
−
(
-3
2
)
=
(
5
2
)
Eine Kombination der vorhergehenden Verfahren benötigt man, um die nachfolgende Aufgabe zu lösen.
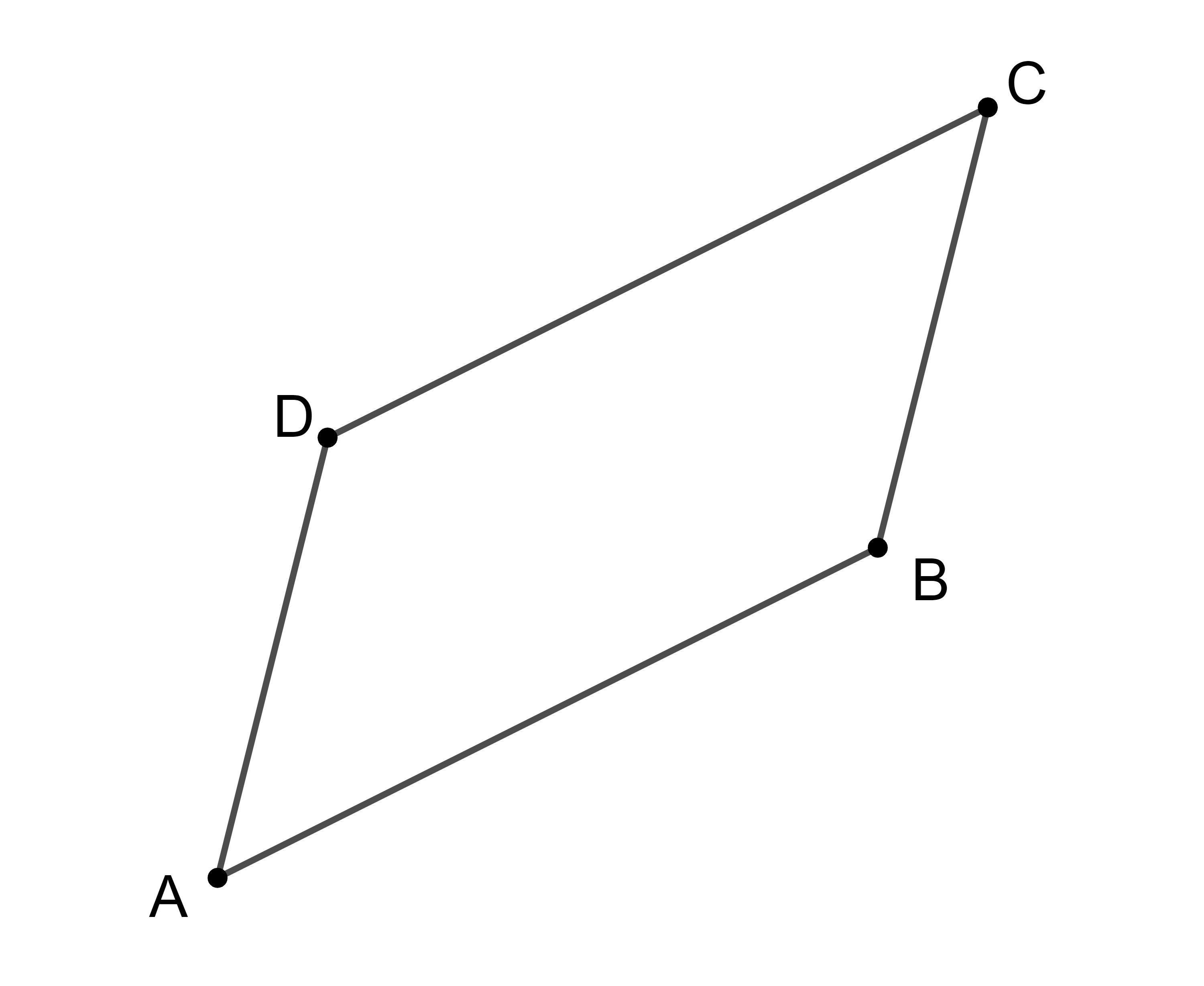
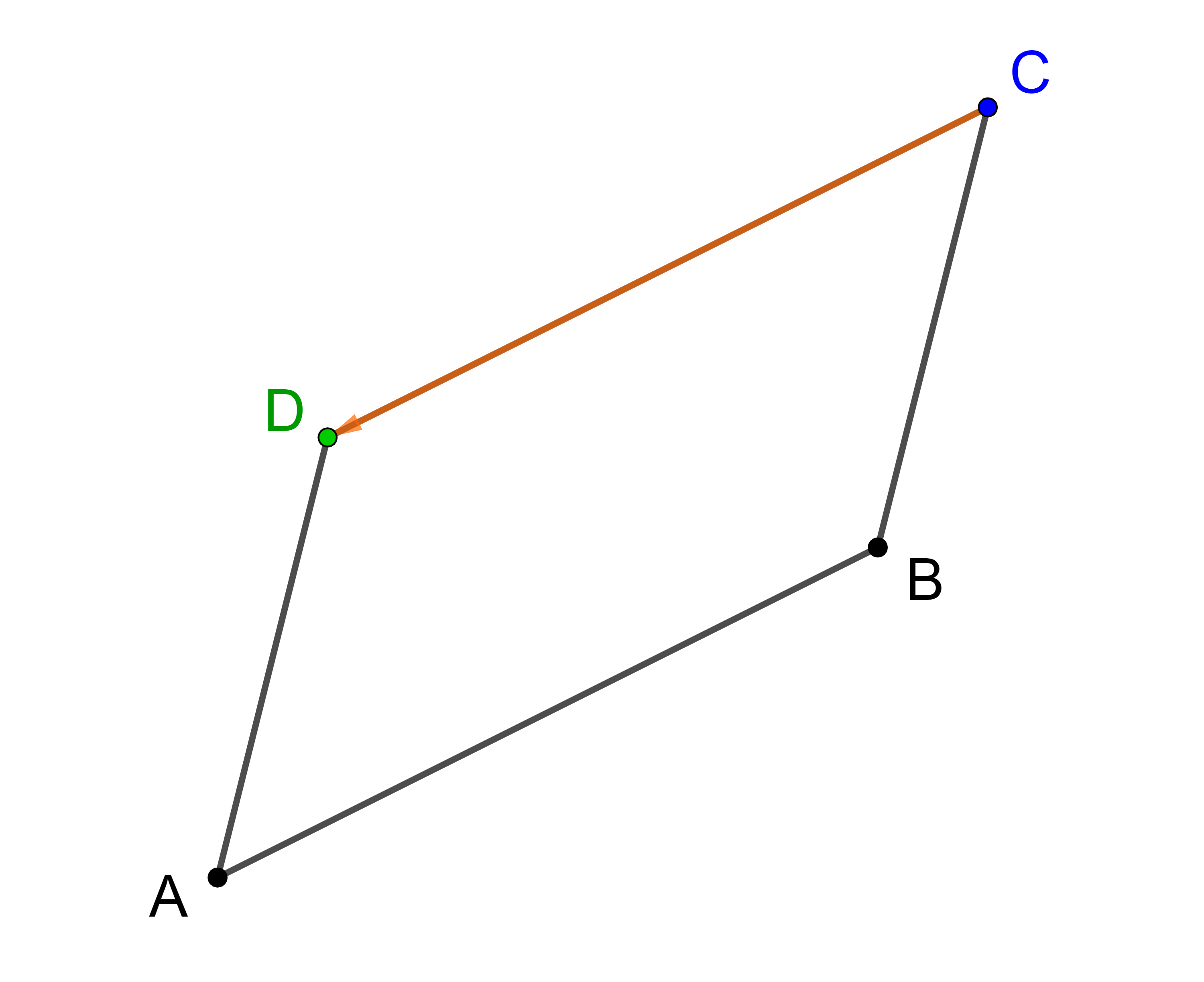
Von einem Parallelogramm mit den Eckpunkten A, B, C und D sind die Punkte A(-4 | -2), B(2 | 1) und C(3 | 5) gegeben. Die Koordinaten des Punktes D sollen rechnerisch ermittelt werden.
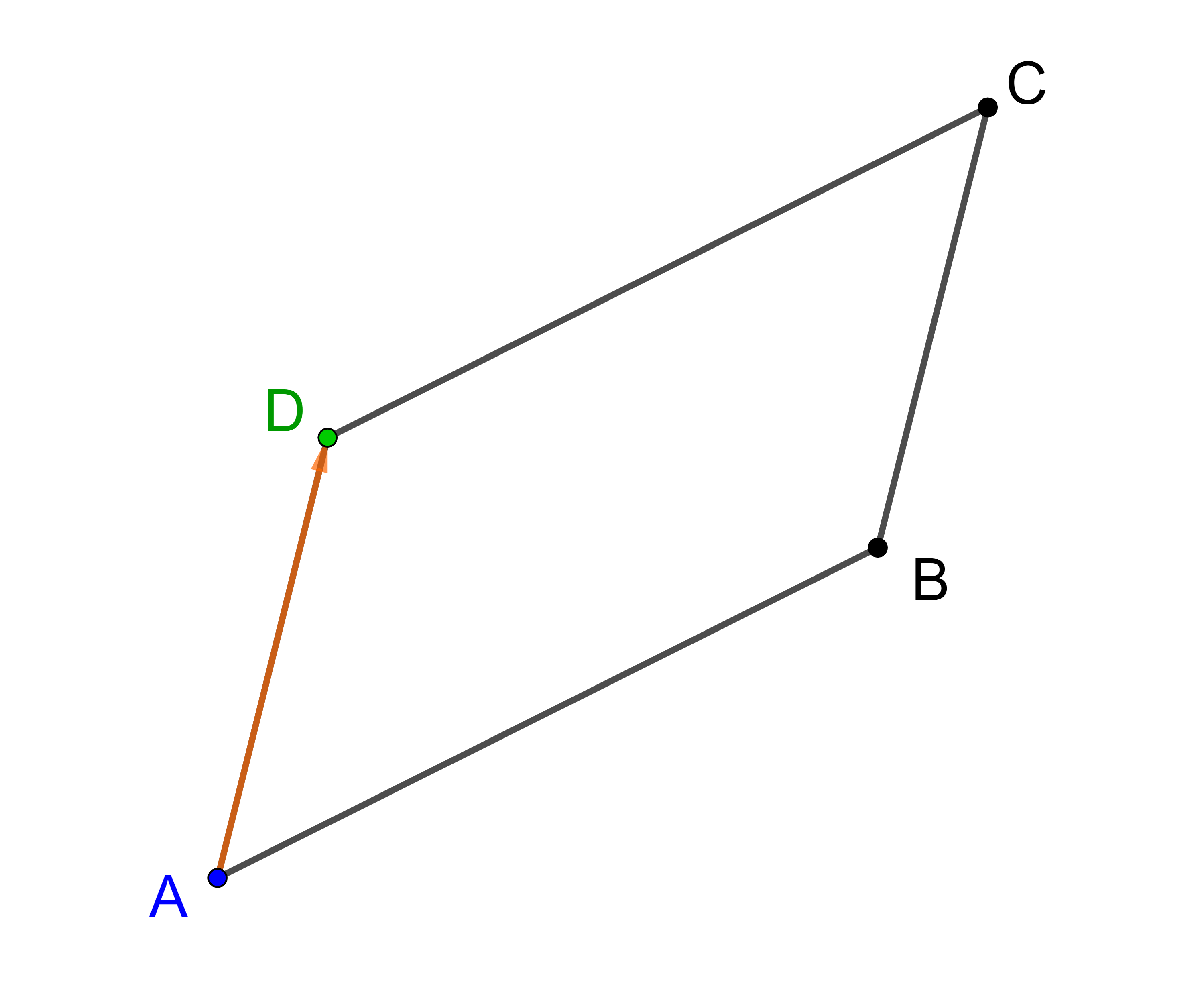
Diese Aufgabe kann gelöst werden, wenn es einen Verbindungsvektor gibt, dessen Koordinaten und Anfangspunkt bekannt sind und dessen Endpunkt der gesuchte Punkt D ist.
Das trifft zum Beispiel auf den Vektor
⟶
AD
zu.
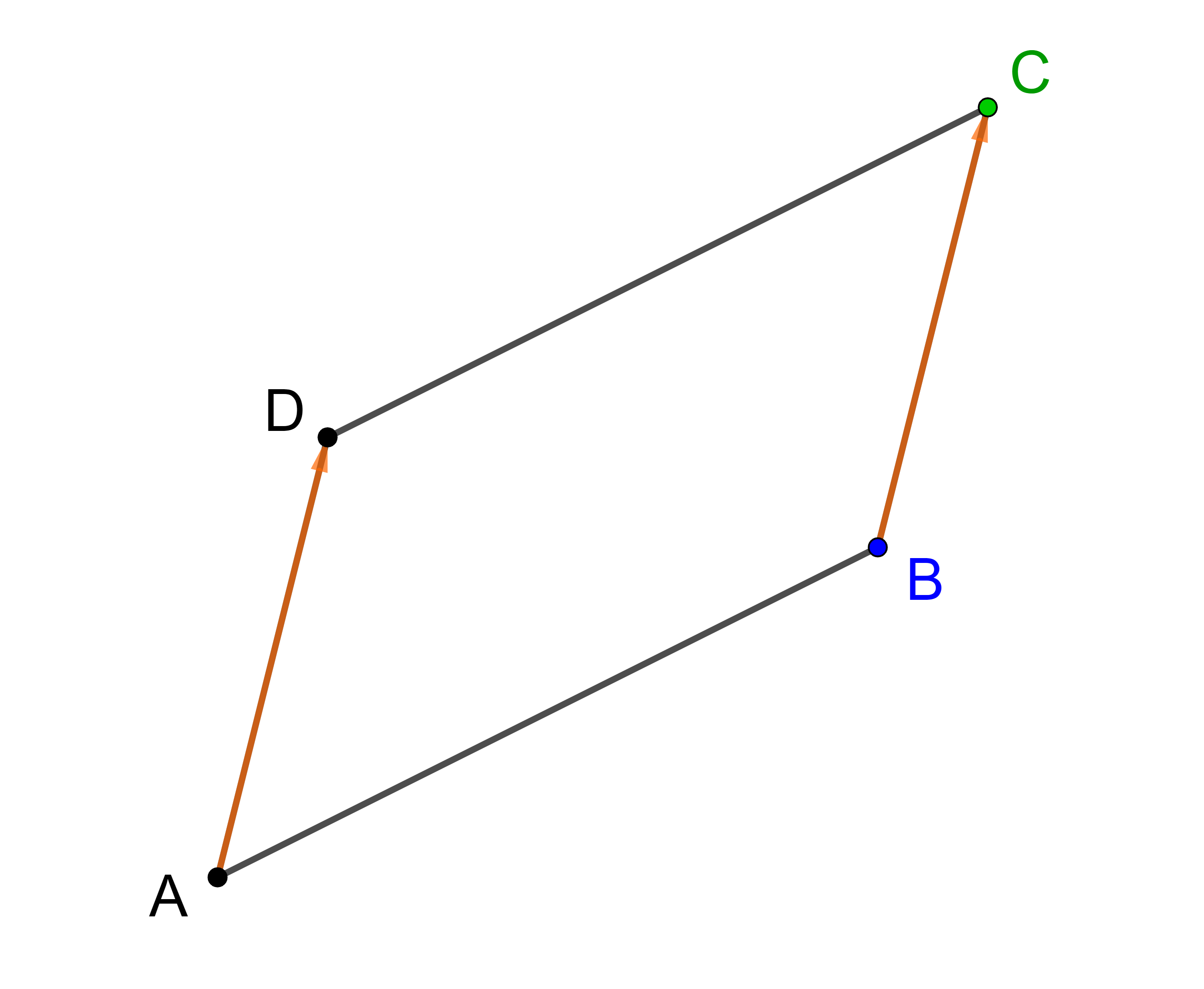
In einem Parallelogramm sind die gegenüberliegenden Seiten parallel und gleich lang.
Daher gilt:
⟶
AD
=
⟶
BC
Die Koordinaten dieses Vektors können berechnet werden, da die Koordinaten der Punkte B und C gegeben sind.
⟶
BC
=
⟶
OC
−
⟶
OB
=
(
3
5
)
−
(
2
1
)
=
(
1
4
)
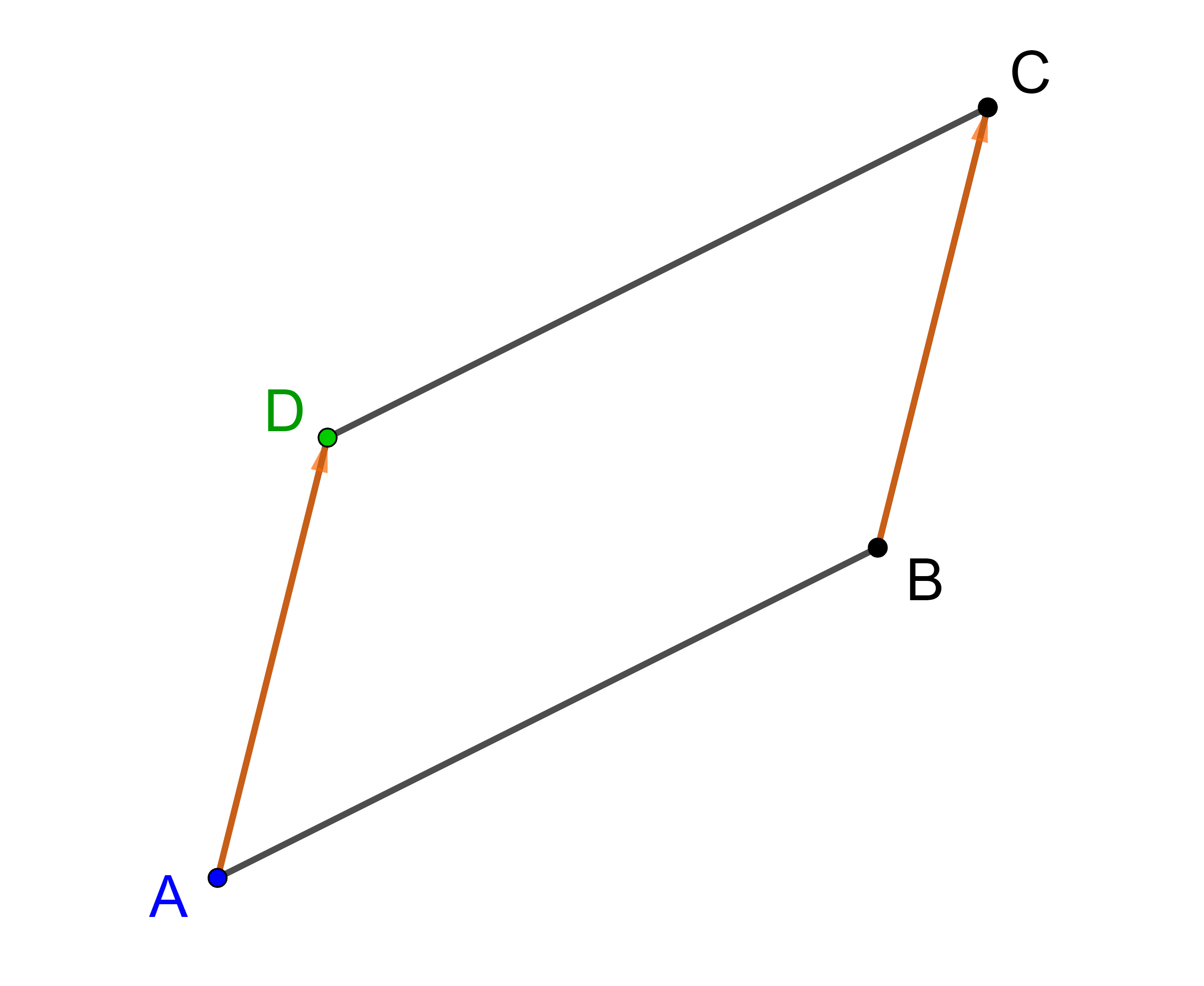
Jetzt können die Koordinaten des Eckpunktes D berechnet werden.
⟶
OD
=
⟶
OA
+
⟶
AD
=
⟶
OA
+
⟶
BC
=
(
-4
-2
)
+
(
1
4
)
=
(
-3
2
)
D(-3 | 2) ist der gesuchte Eckpunkt.
Die Aufgabe kann auch mit Hilfe eines anderen Verbindungsvektors gelöst werden.
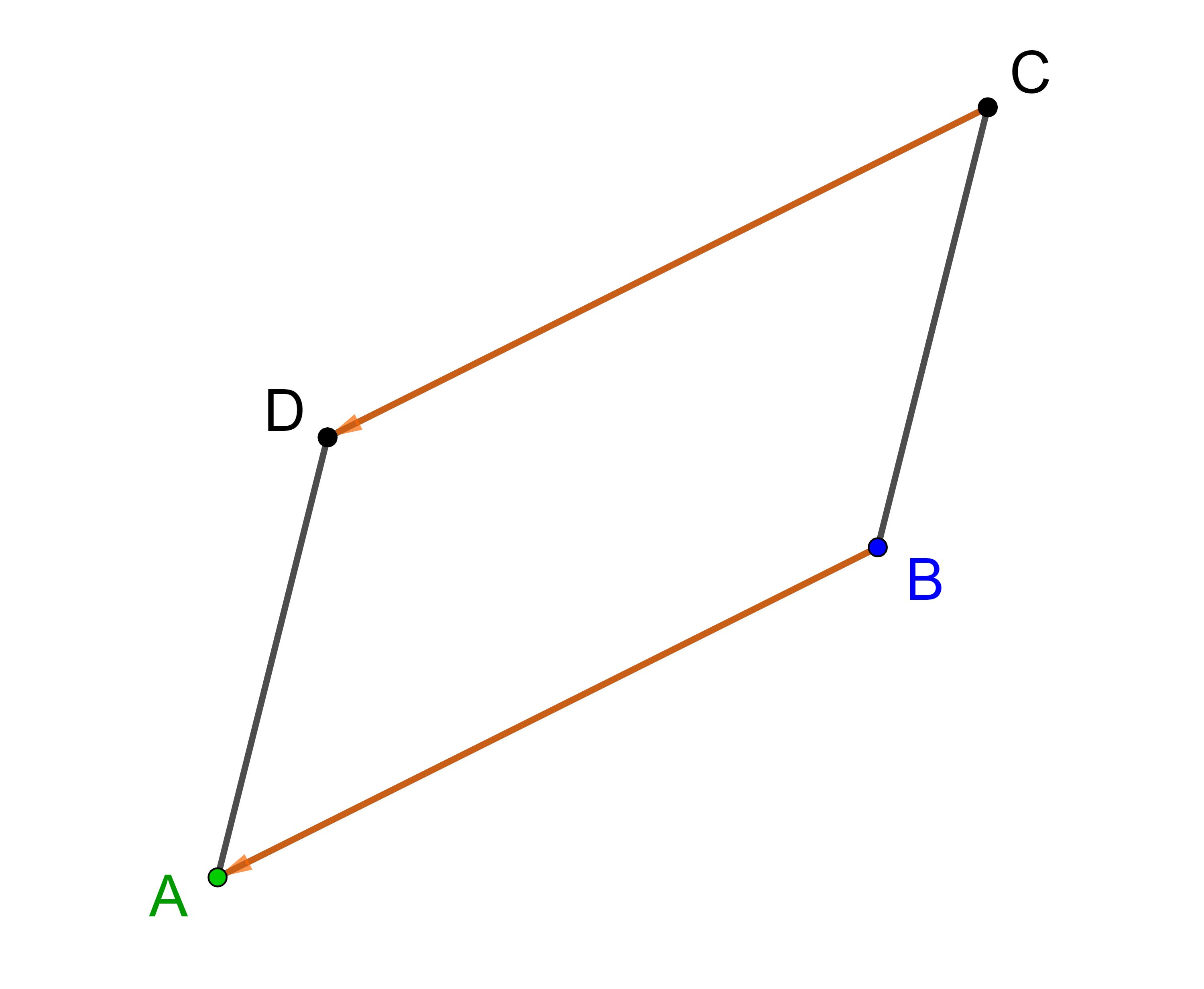
⟶
CD
=
⟶
BA
⟶
BA
=
⟶
OA
−
⟶
OB
=
(
-4
-2
)
−
(
2
1
)
=
(
-6
-3
)
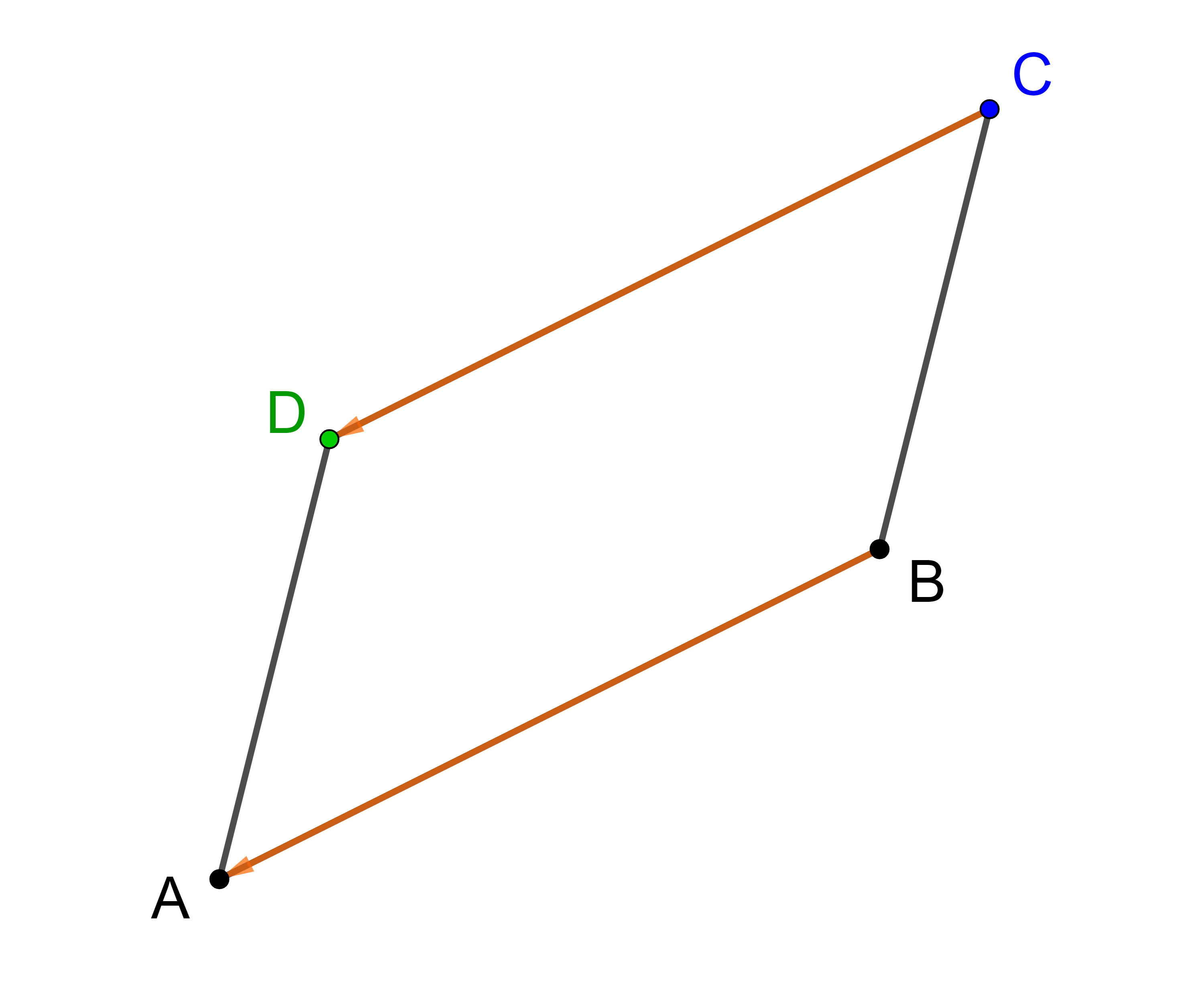
⟶
OD
=
⟶
OC
+
⟶
CD
=
⟶
OC
+
⟶
BA
=
(
3
5
)
+
(
-6
-3
)
=
(
-3
2
)
D(-3 | 2) ist der gesuchte Eckpunkt.
Übung 1:
Gegeben sind die Punkte
A
(
3
|
-6
)
und
B
(
5
|
4
).
Berechnen Sie die Koordinaten des angegebenen Vektors mit Hilfe von Ortsvektoren.
⟶
A
B
=
⟶
−
⟶
=
(
)
−
(
)
=
(
)
Übung 2:
Von einem Parallelogramm mit den Eckpunkten A, B, C und D sind die folgenden Punkte gegeben:
A(
2
|
3
)
,
B(
6
|
2
)
und
C(
8
|
5
)
.
Berechnen Sie die Koordinaten des fehlenden Eckpunktes mit Hilfe von Ortsvektoren.
⟶
=
⟶
+
⟶
=
⟶
+
⟶
=
(
)
+
(
)
=
(
)
(
|
)
ist der gesuchte Eckpunkt des Parallelogramms.