4. Bestimmung von Punktkoordinaten mit Hilfe von Ortsvektoren

← Kapitelübersicht
4.2.  Mittelpunkt einer Strecke
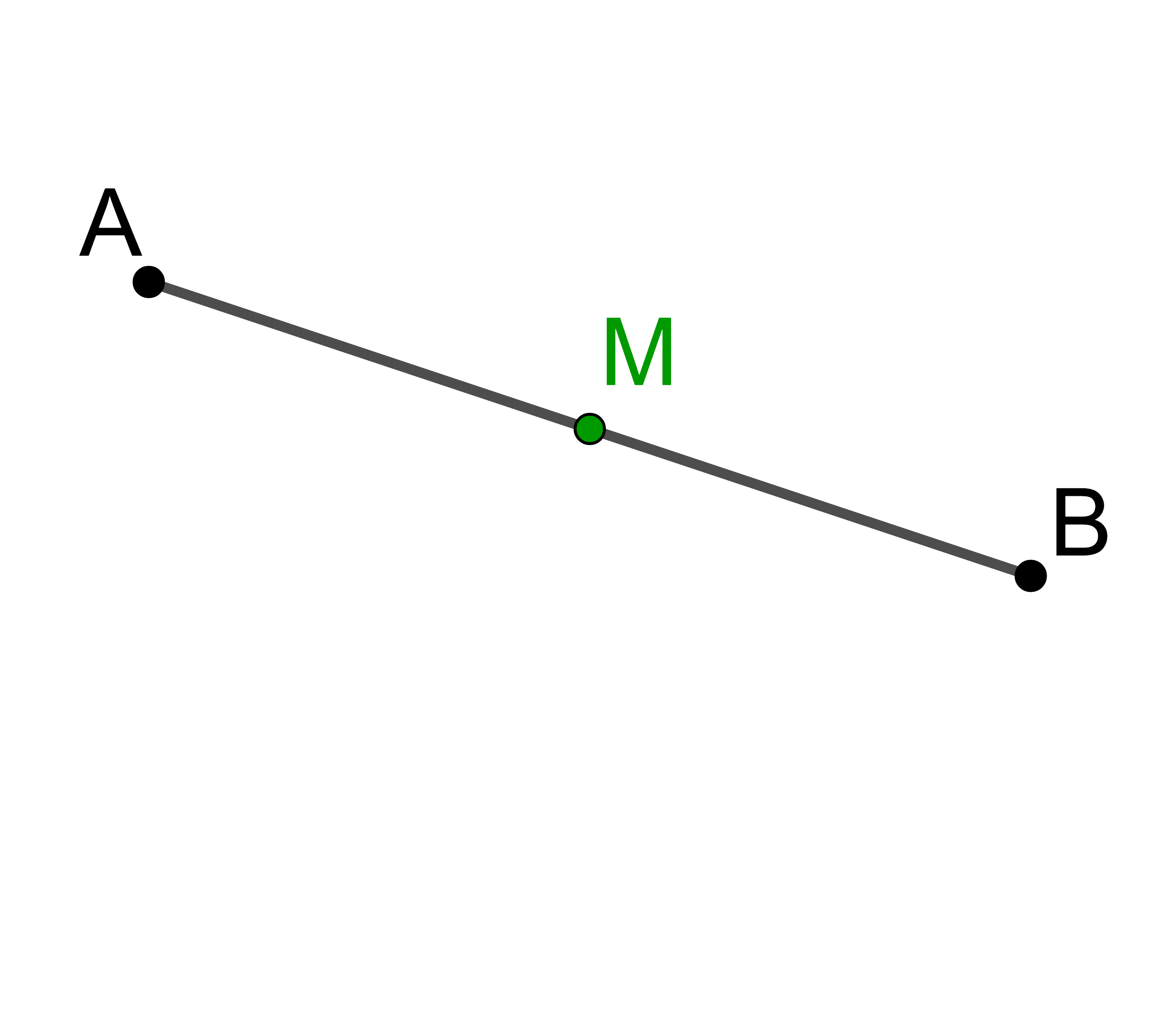
In diesem Kapitel wird erklärt, wie man den Mittelpunkt einer in der Ebene oder im Raum gelegenen Strecke mit Hilfe von Vektoren bestimmen kann.
Gegeben sind die Punkte A(-1 | 4) und B(5 | 2).

Der Mittelpunkt M der Strecke AB soll rechnerisch mit Hilfe von Vektoren ermittelt werden.
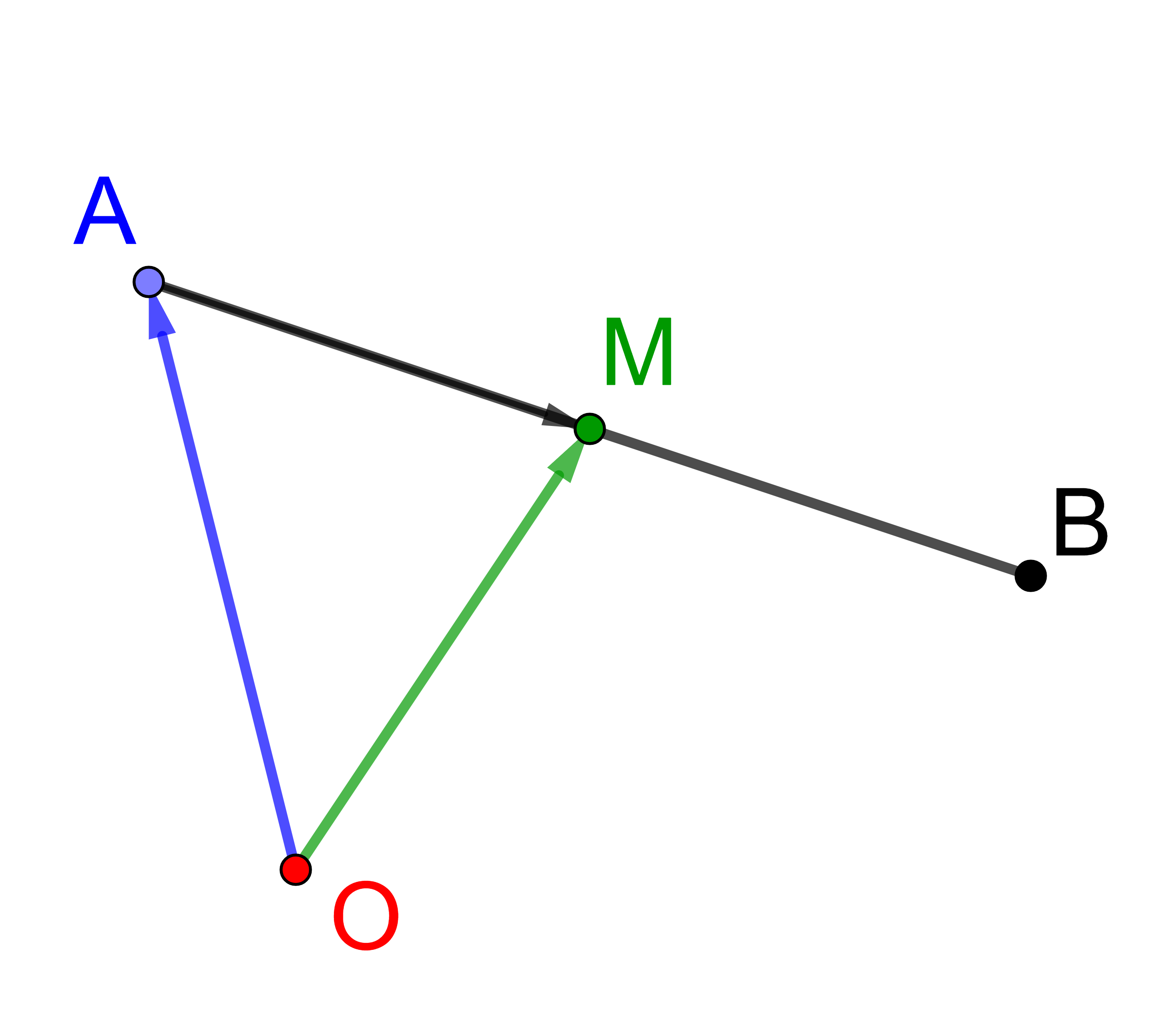
Es gilt:
⟶
OM
=
⟶
OA
+
⟶
AM
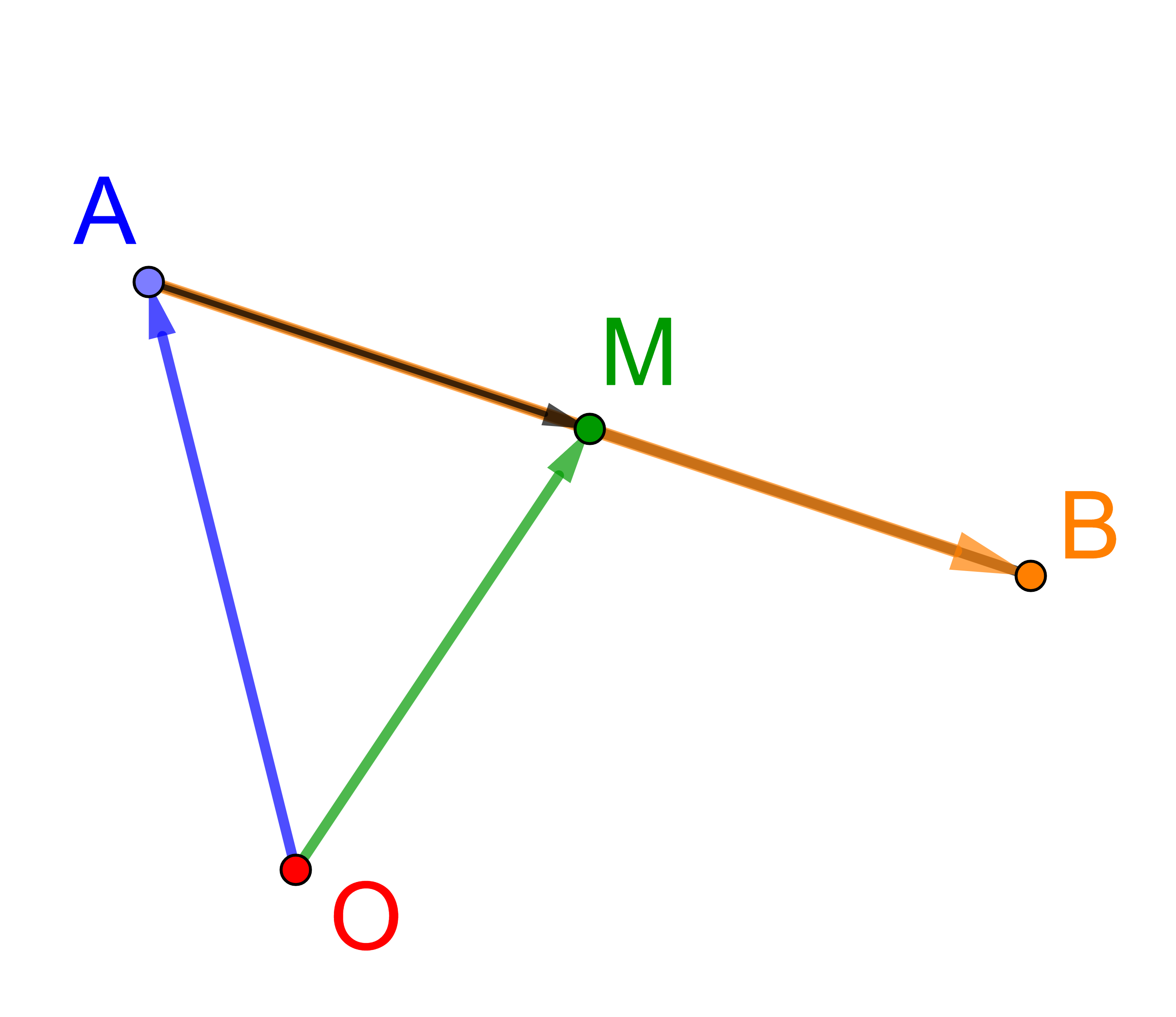
Da M der Mittelpunkt der Strecke AB ist, gilt:
⟶
AM
=
1
2
⋅
⟶
AB
und somit:


⟶
OM
=
⟶
OA
+
1
2
⋅
⟶
AB
=
(
-1
 4
)
+
1
2
⋅
(
 6
-2
)
=
(
-1
 4
)
+
(
 3
-1
)
=
(
2
3
)



M(2 | 3) ist der Mittelpunkt der Strecke AB.
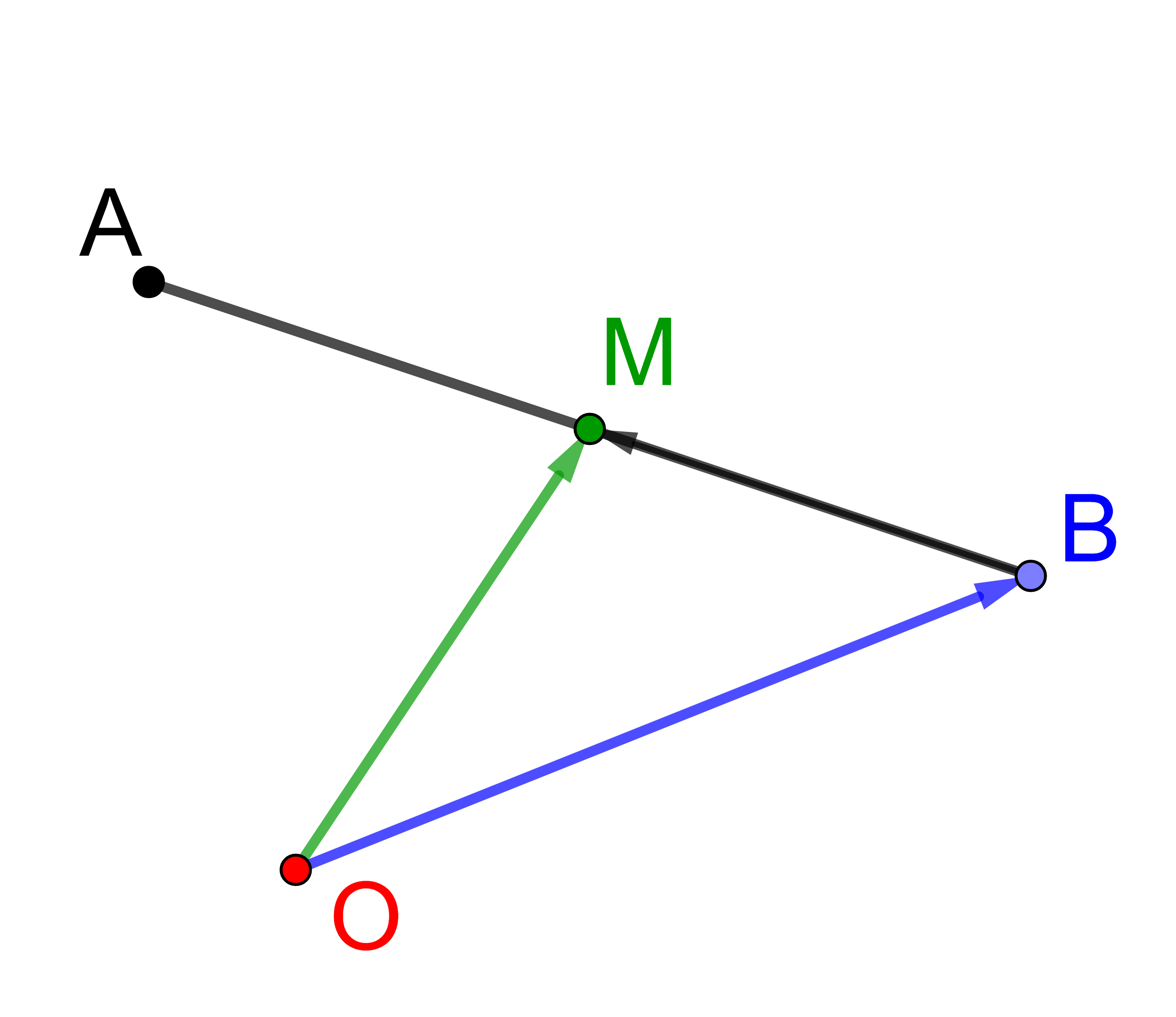
Auch der Punkt B kann als sogenannter Aufpunkt zur Bestimmung des Streckenmittelpunktes M verwendet werden:
⟶
OM
=
⟶
OB
+
⟶
BM
⟶
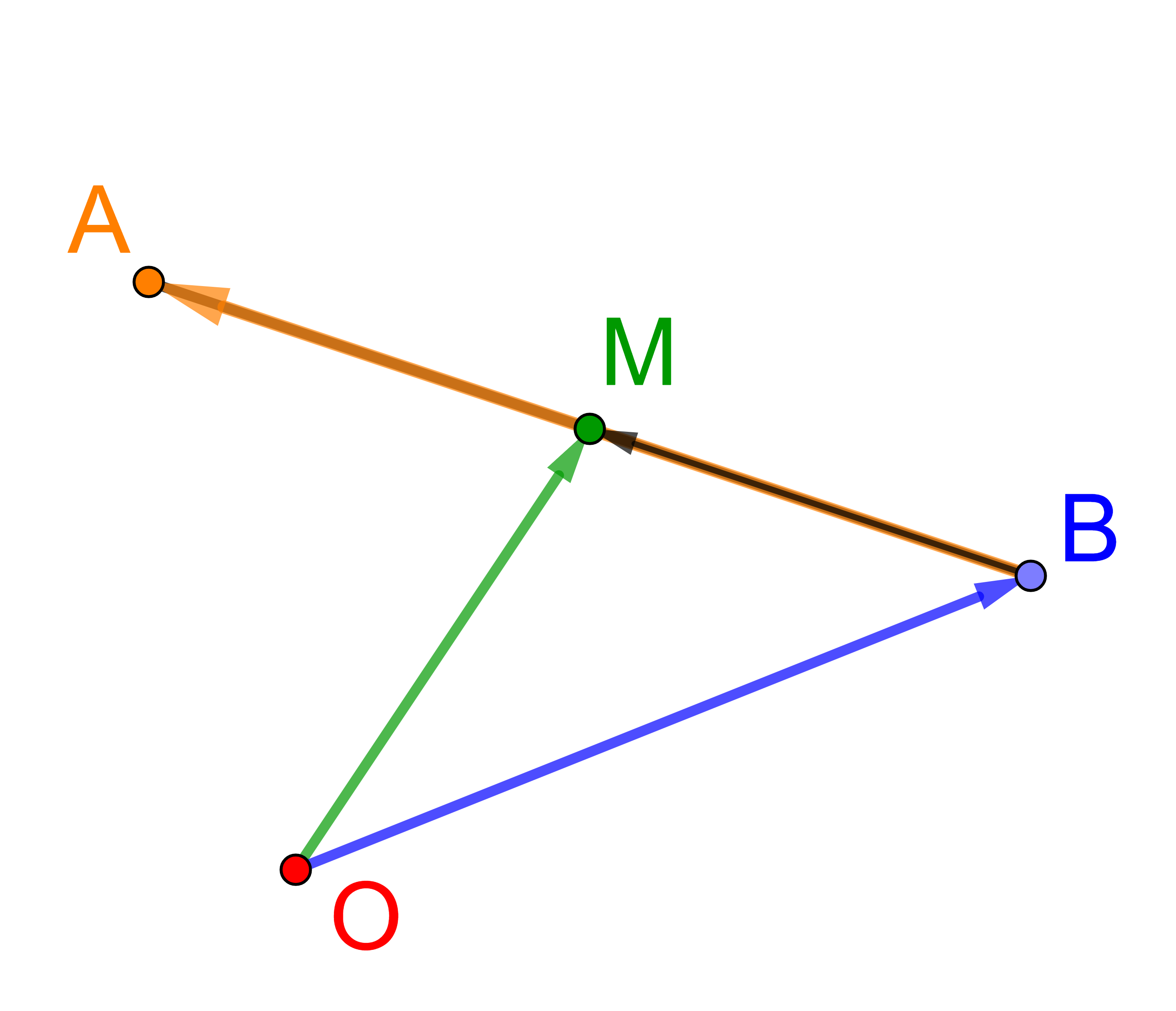
BM
=
1
2
⋅
⟶
BA
Somit gilt:


⟶
OM
=
⟶
OB
+
1
2
⋅
⟶
BA
=
(
5
2
)
+
1
2
⋅
(
-6
 2
)
=
(
5
2
)
+
(
-3
 1
)
=
(
2
3
)



M(2 | 3) ist der Mittelpunkt der Strecke AB.
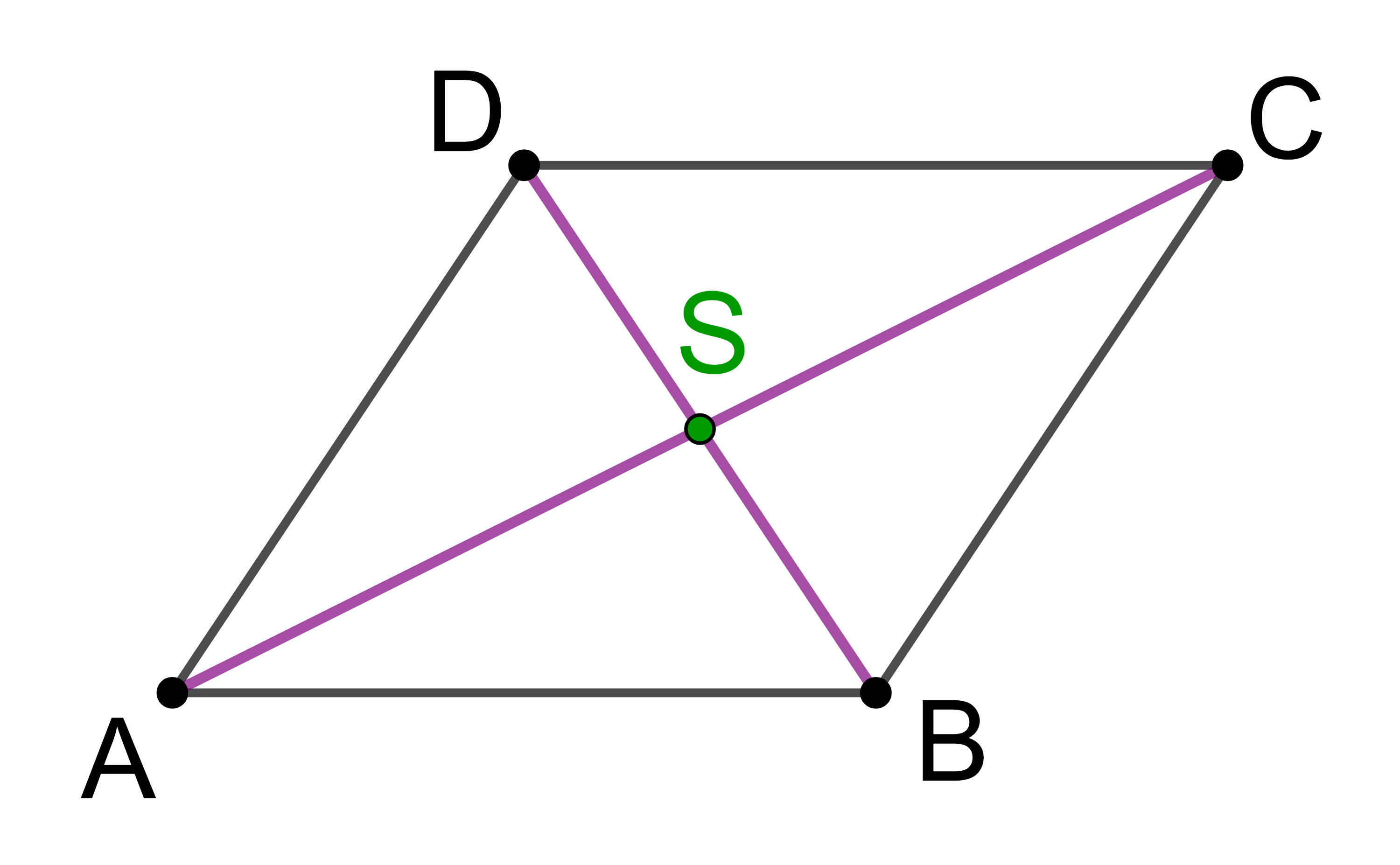
In jedem Parallelogramm schneiden sich die Diagonalen in einem Punkt S. Der Schnittpunkt S ist der Mittelpunkt jeder Diagonalen. Sind die Koordinaten der Eckpunkte A, B, C und D des Parallelogramms bekannt, können die Koordinaten des Schnittpunktes S mit Hilfe von Vektoren berechnet werden.
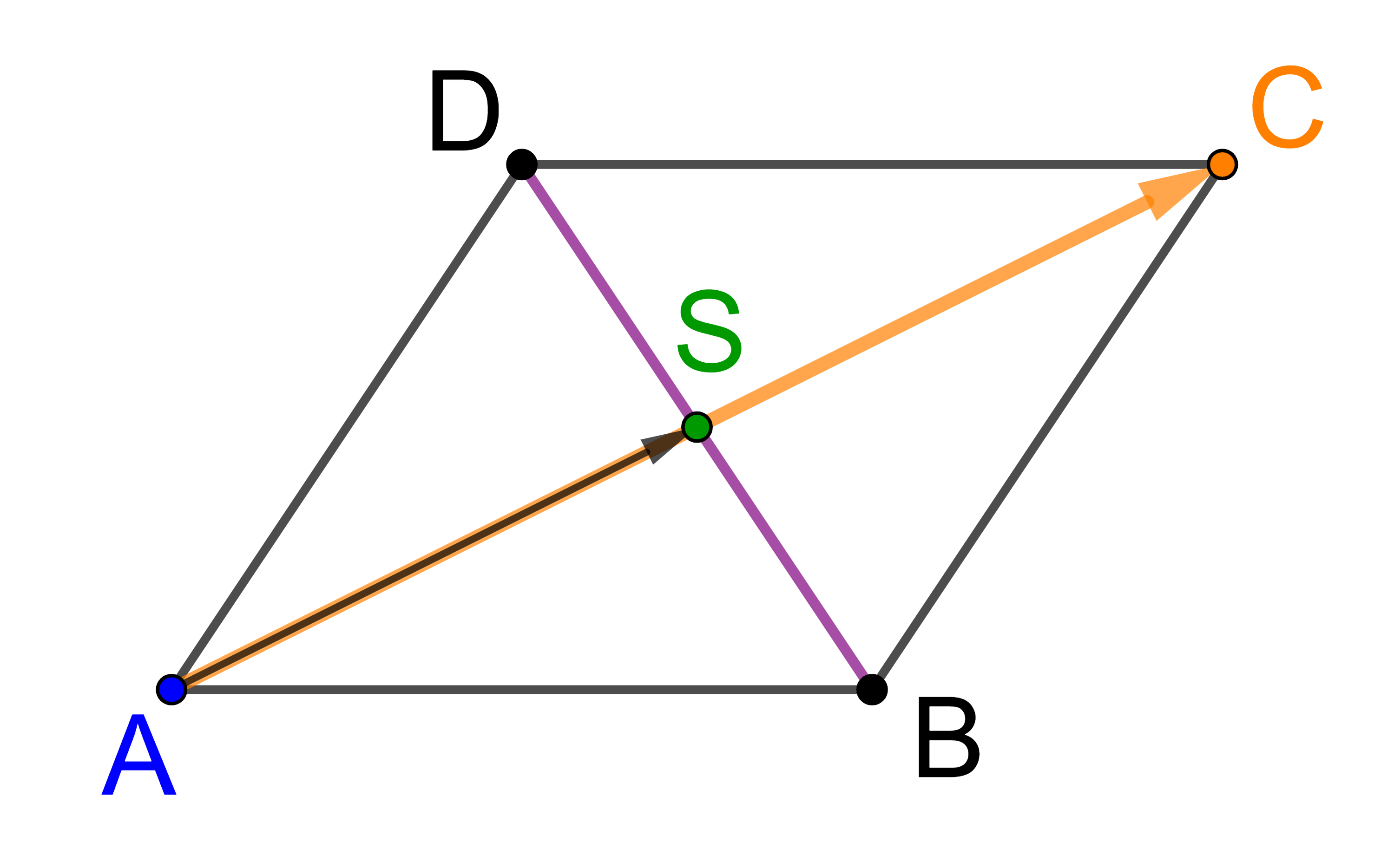
Da S der Mittelpunkt der Strecke AC ist, gilt:
⟶
OS
=
⟶
OA
+
1
2
⋅
⟶
AC
(oder:   
⟶
OS
=
⟶
OC
+
1
2
⋅
⟶
CA
)
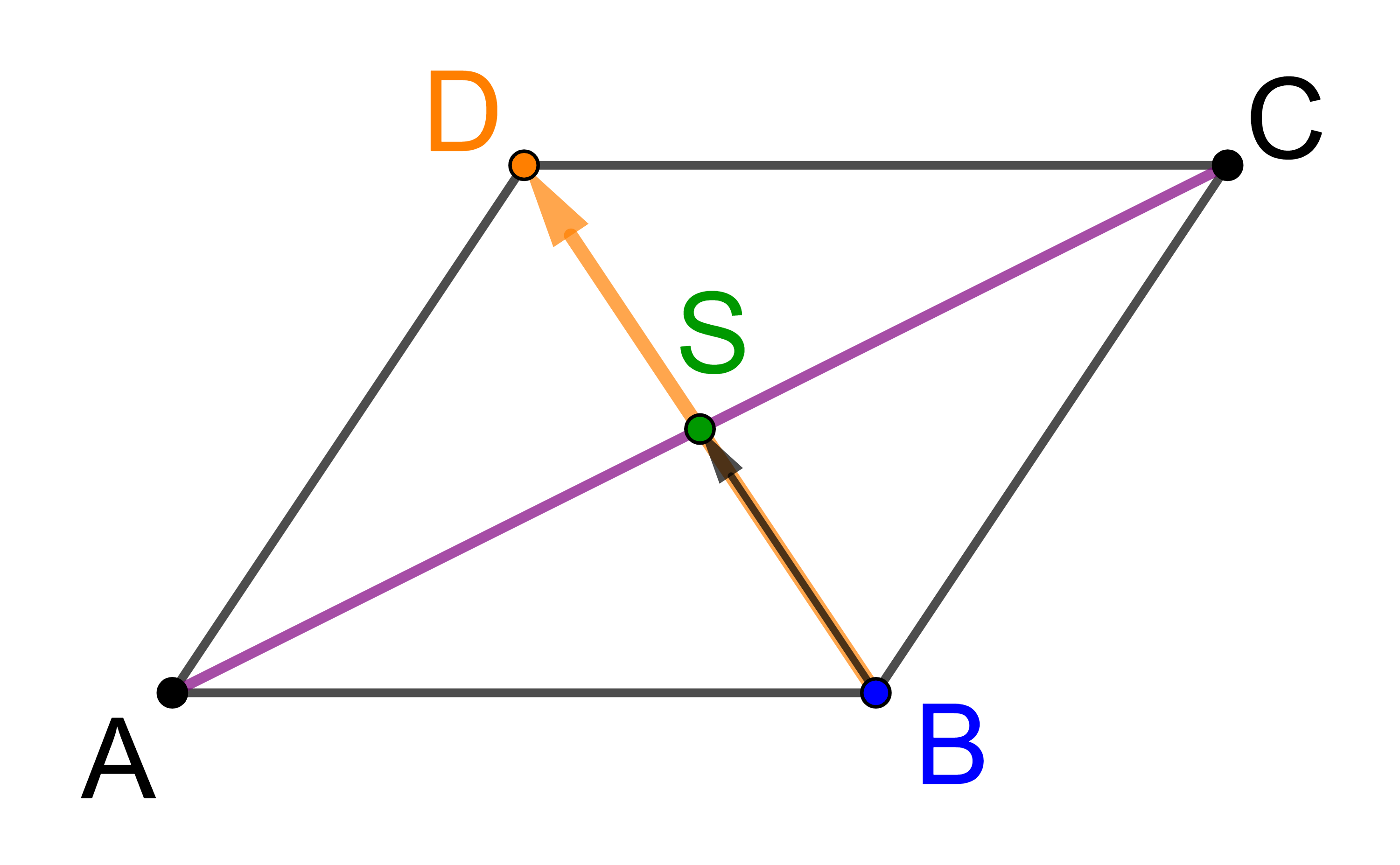
Ebenso kann man die Koordinaten von S mit Hilfe der Eckpunkte B und D berechnen:
⟶
OS
=
⟶
OB
+
1
2
⋅
⟶
BD
(oder:   
⟶
OS
=
⟶
OD
+
1
2
⋅
⟶
DB
)
Das Verfahren zur Bestimmung des Mittelpunktes einer Strecke kann auf beliebige Teilungspunkte übertragen werden.
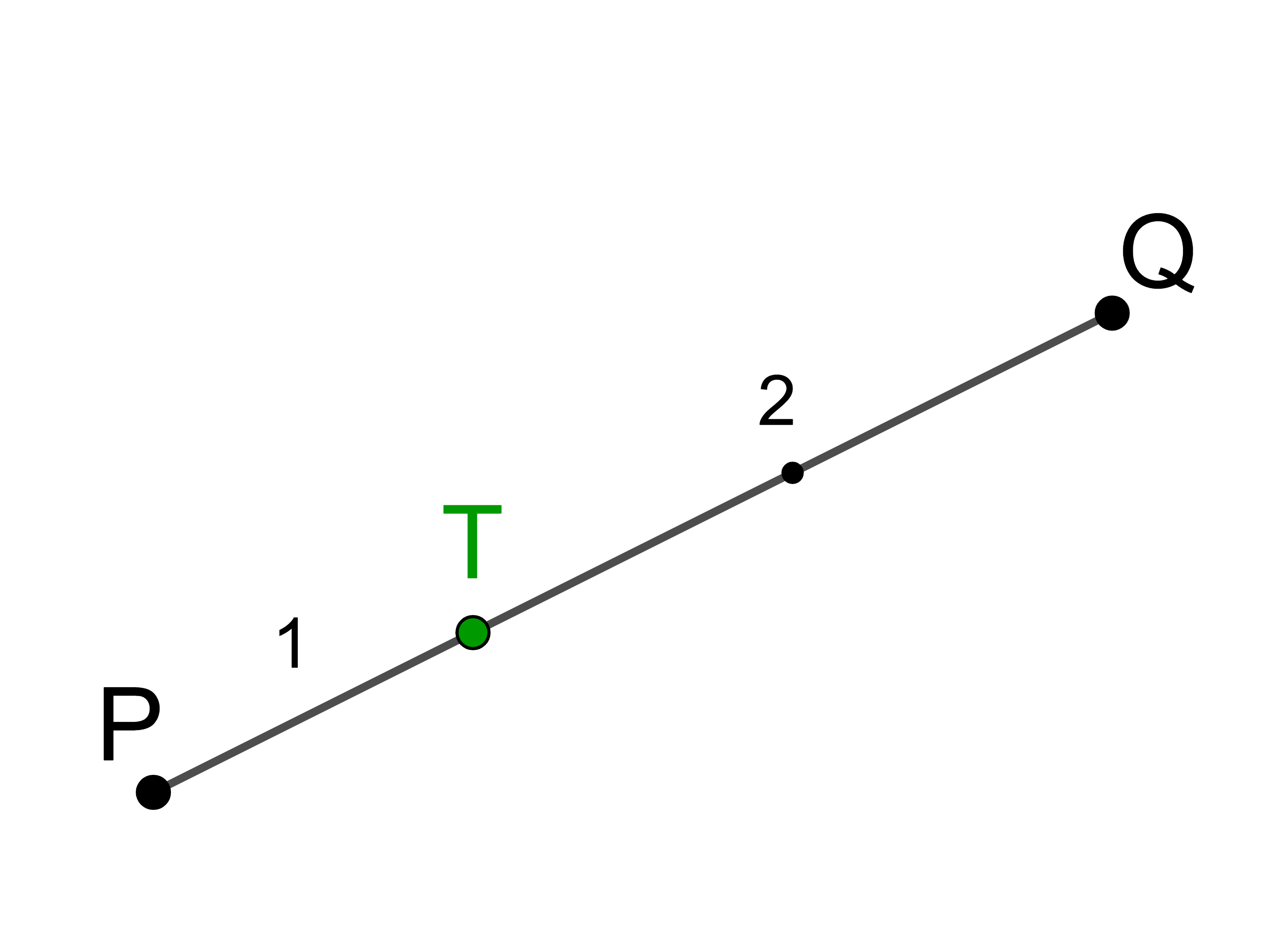
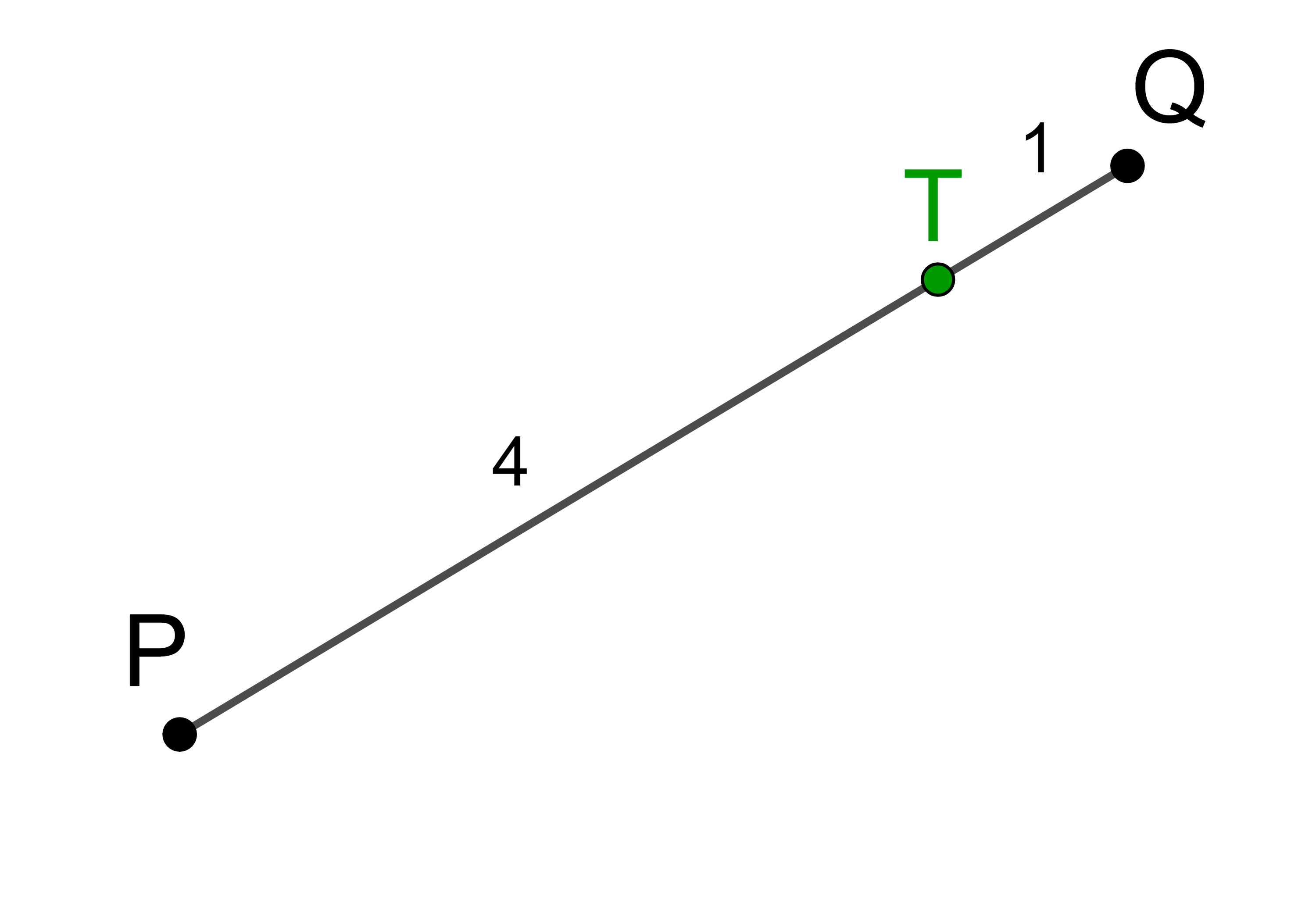
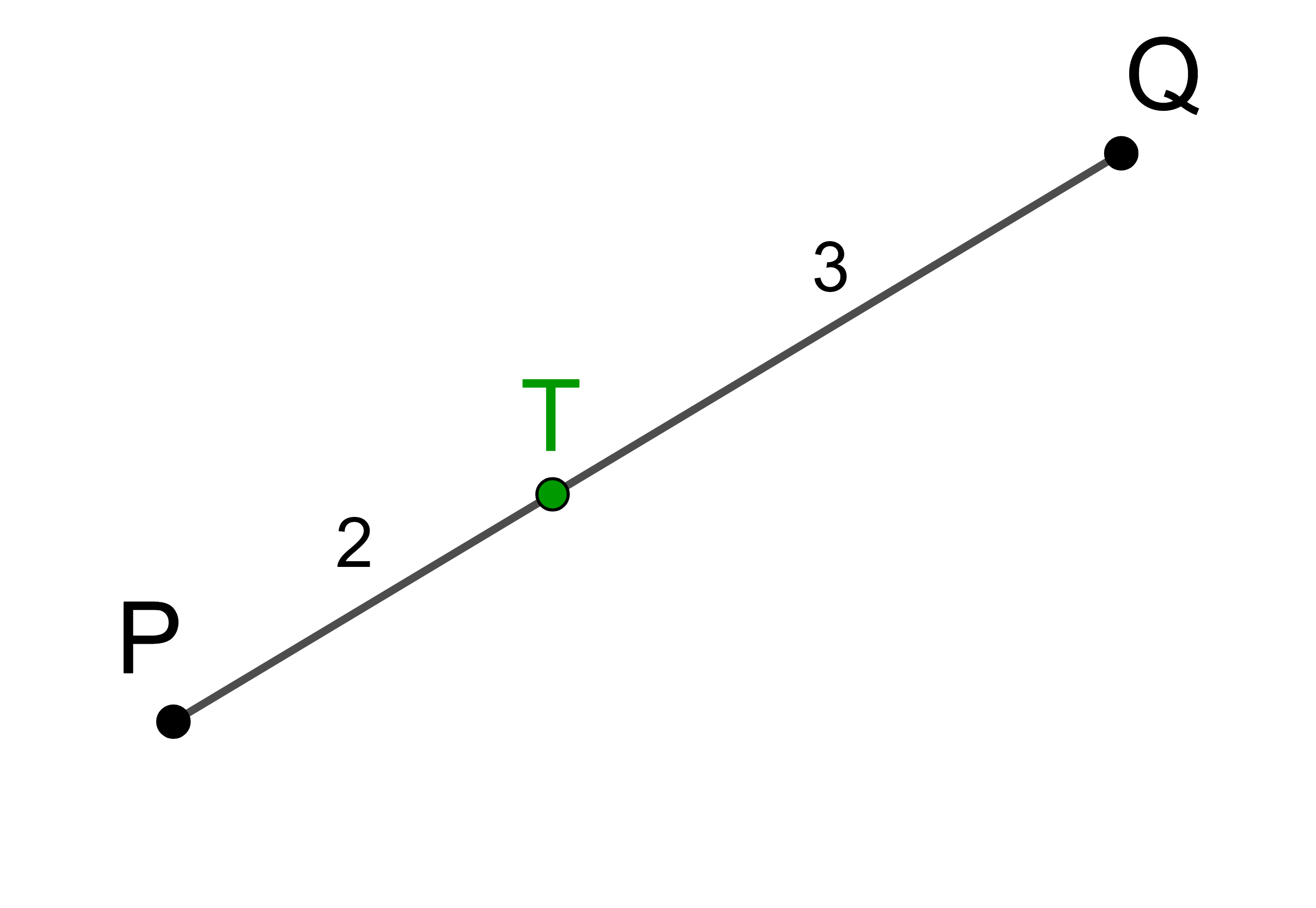
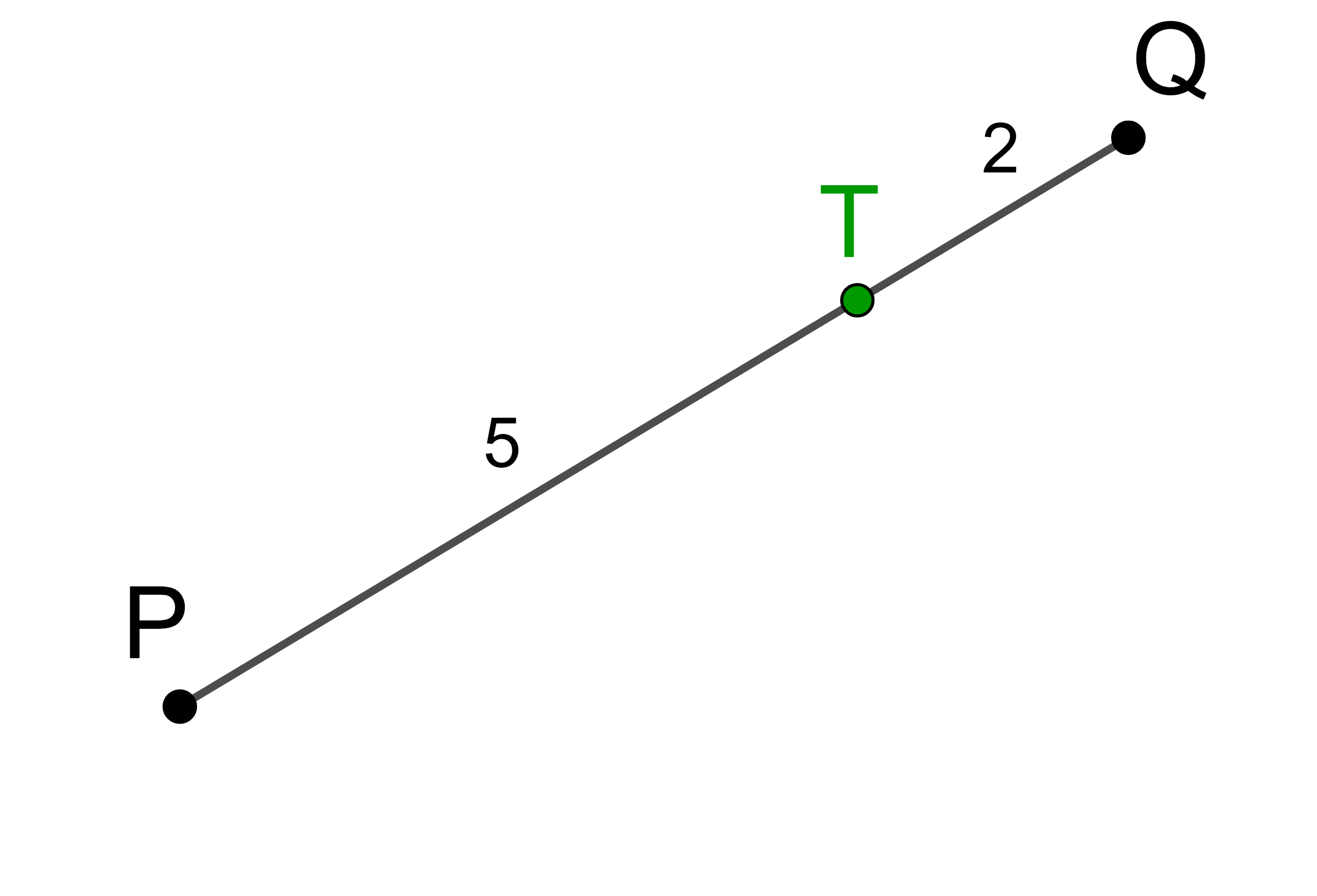
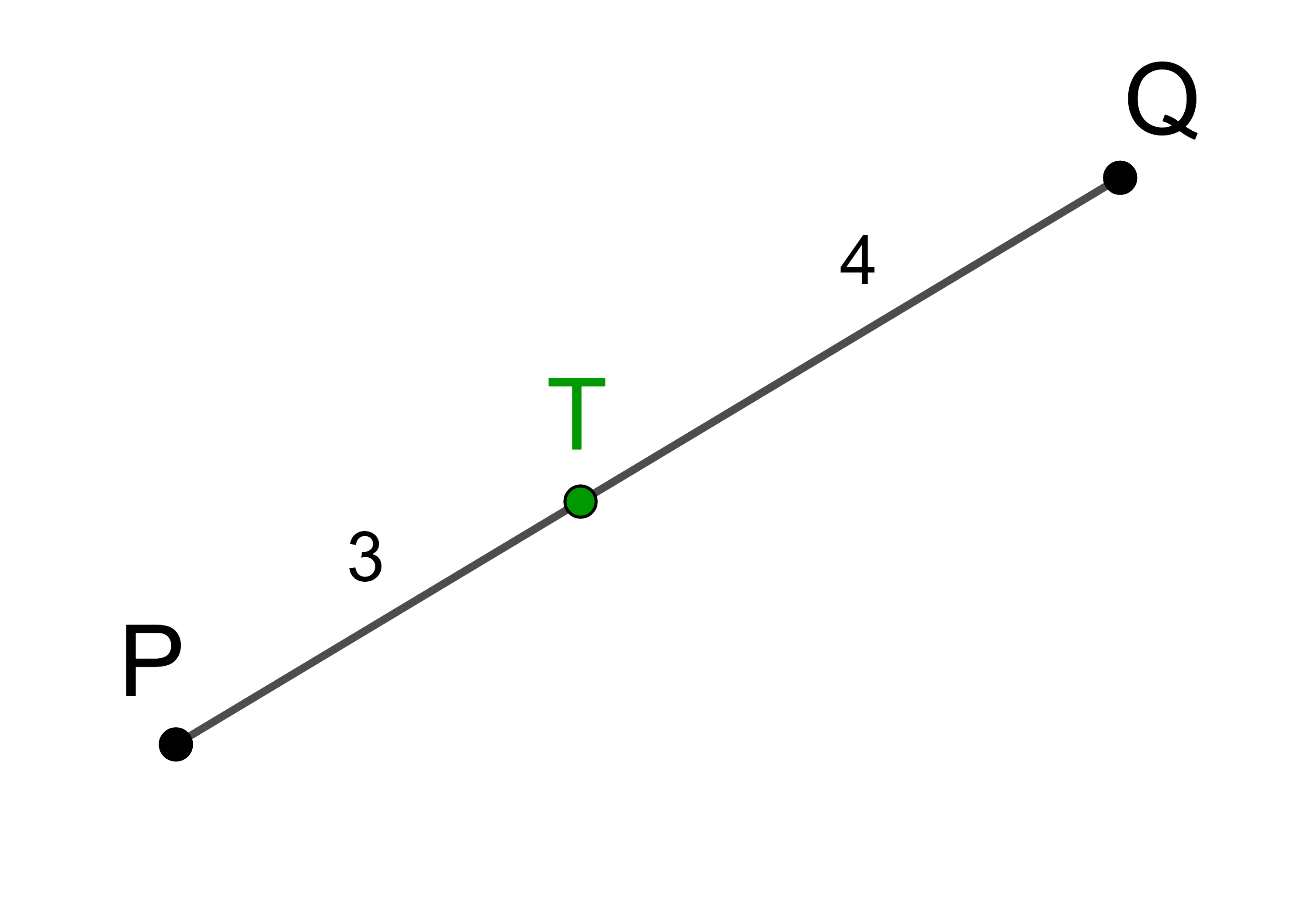
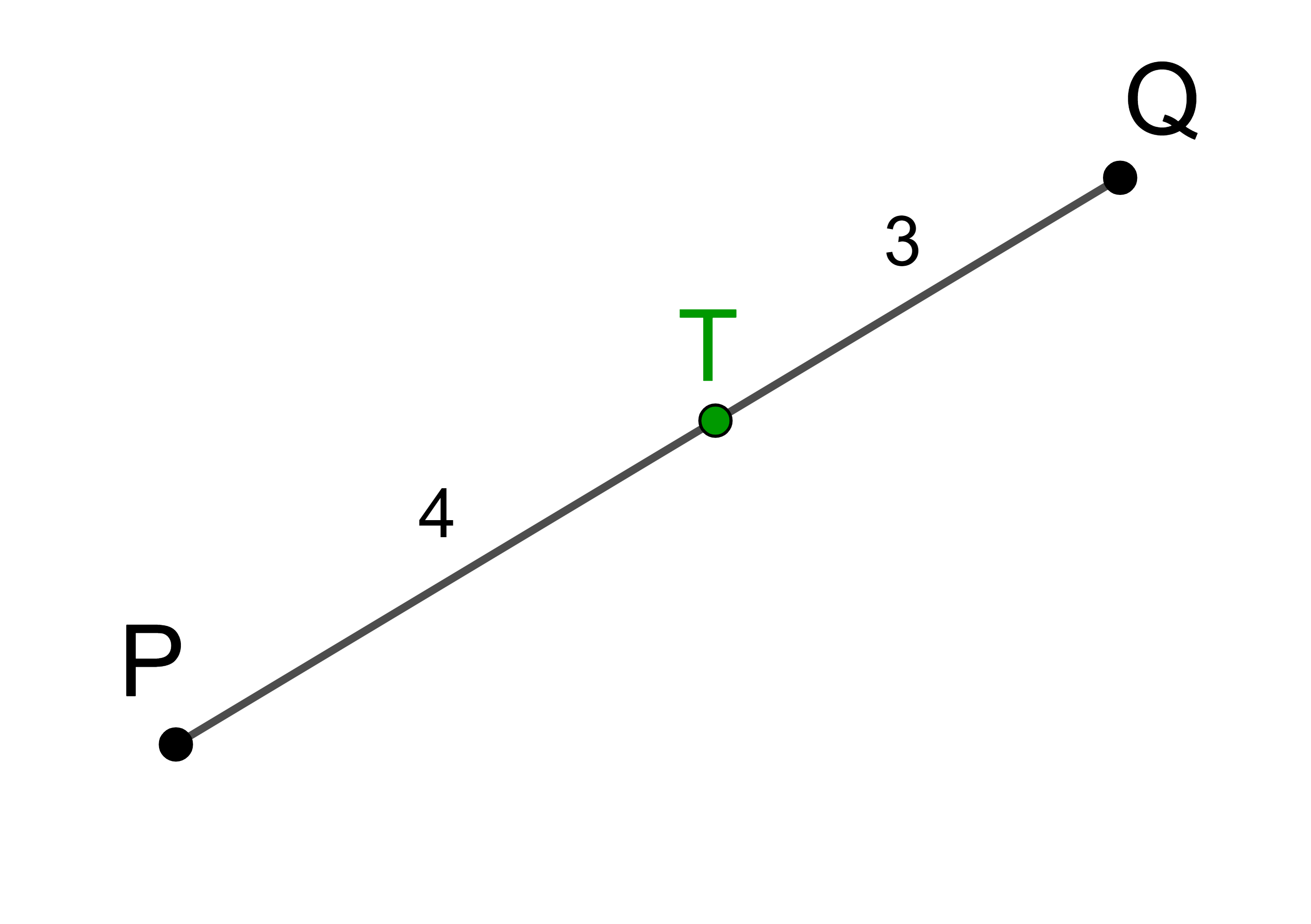
Gegeben sind die Punkte P(-2 | 4 | 7) und Q(7 | 16 | -8) im Raum.


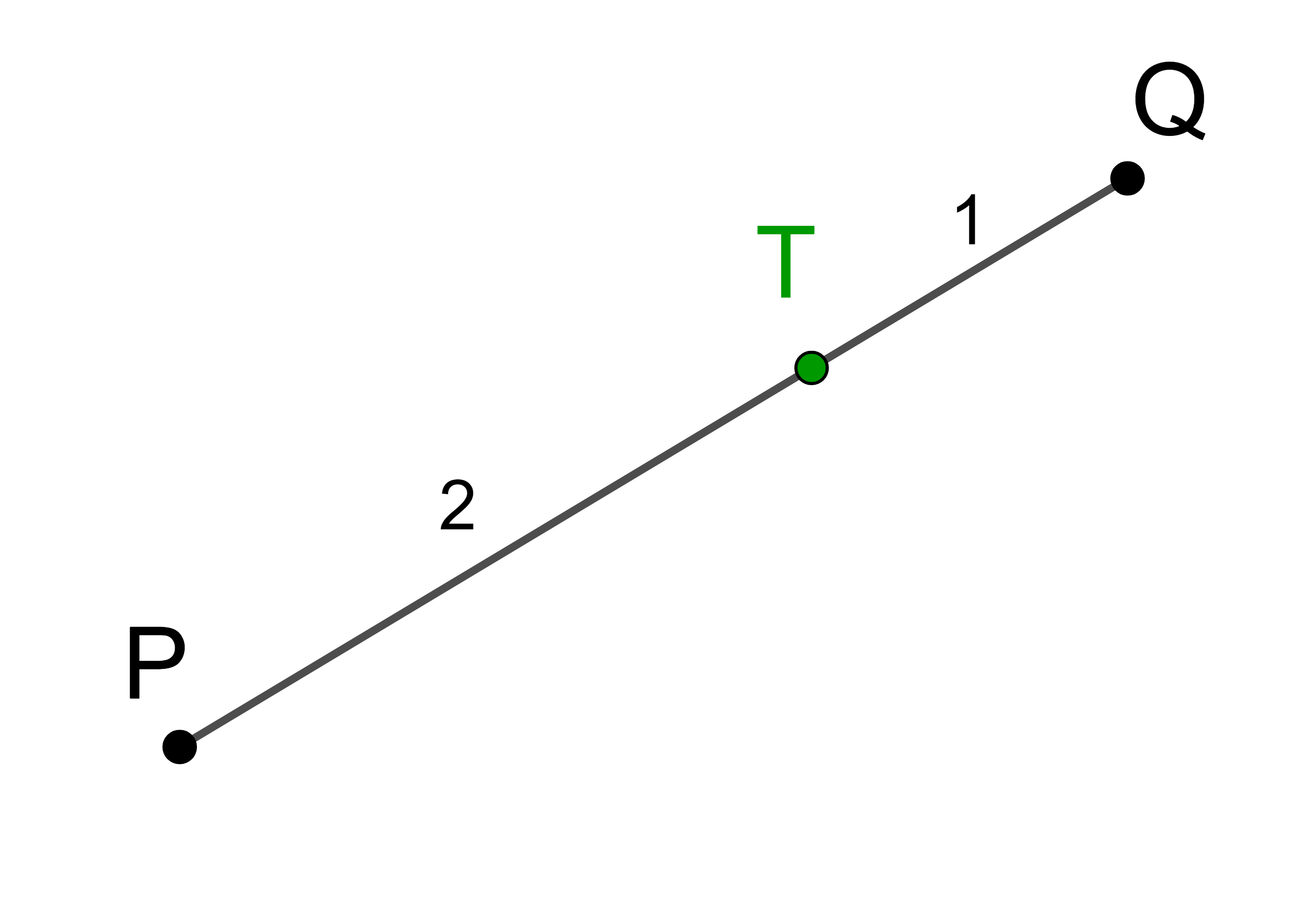
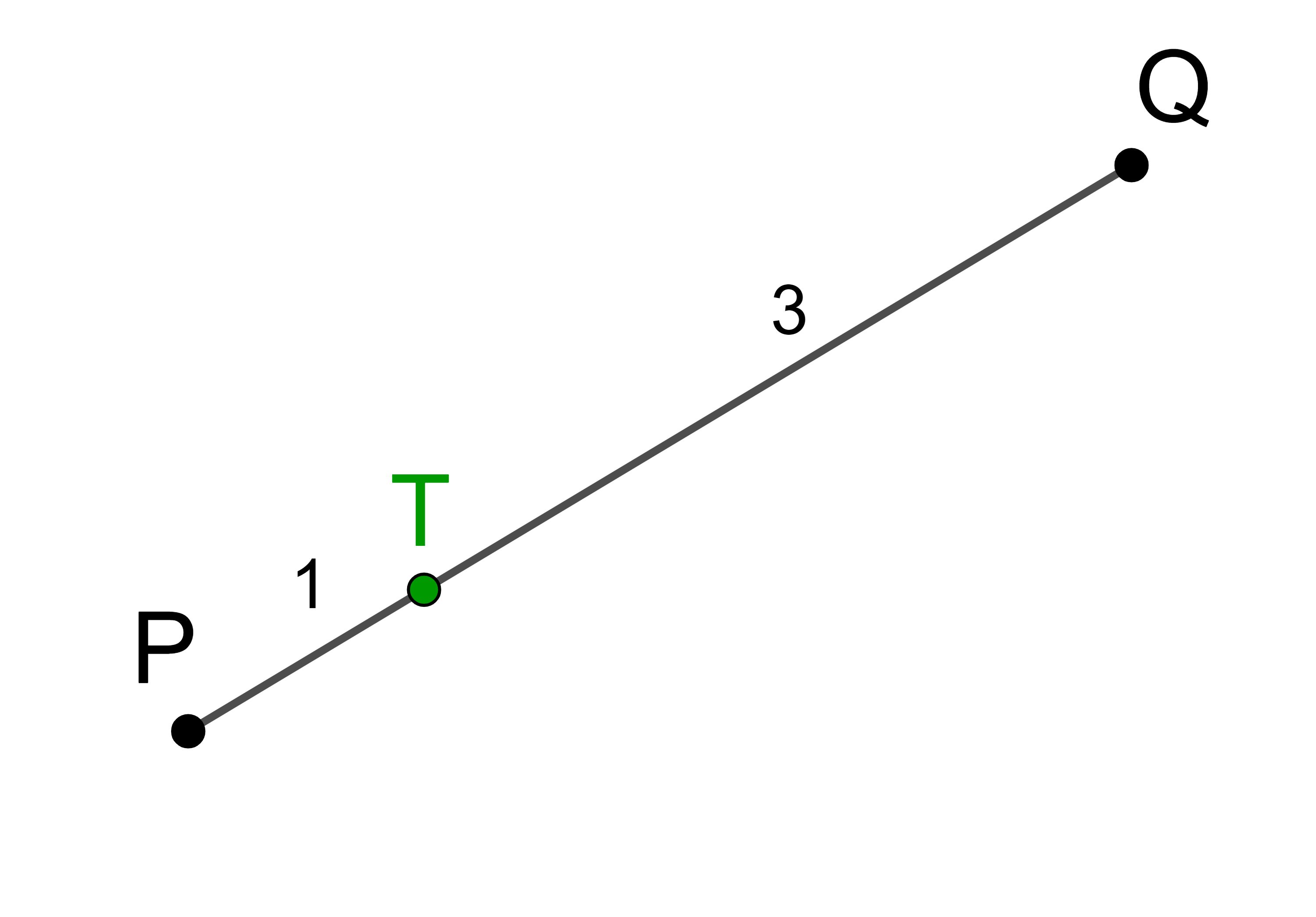
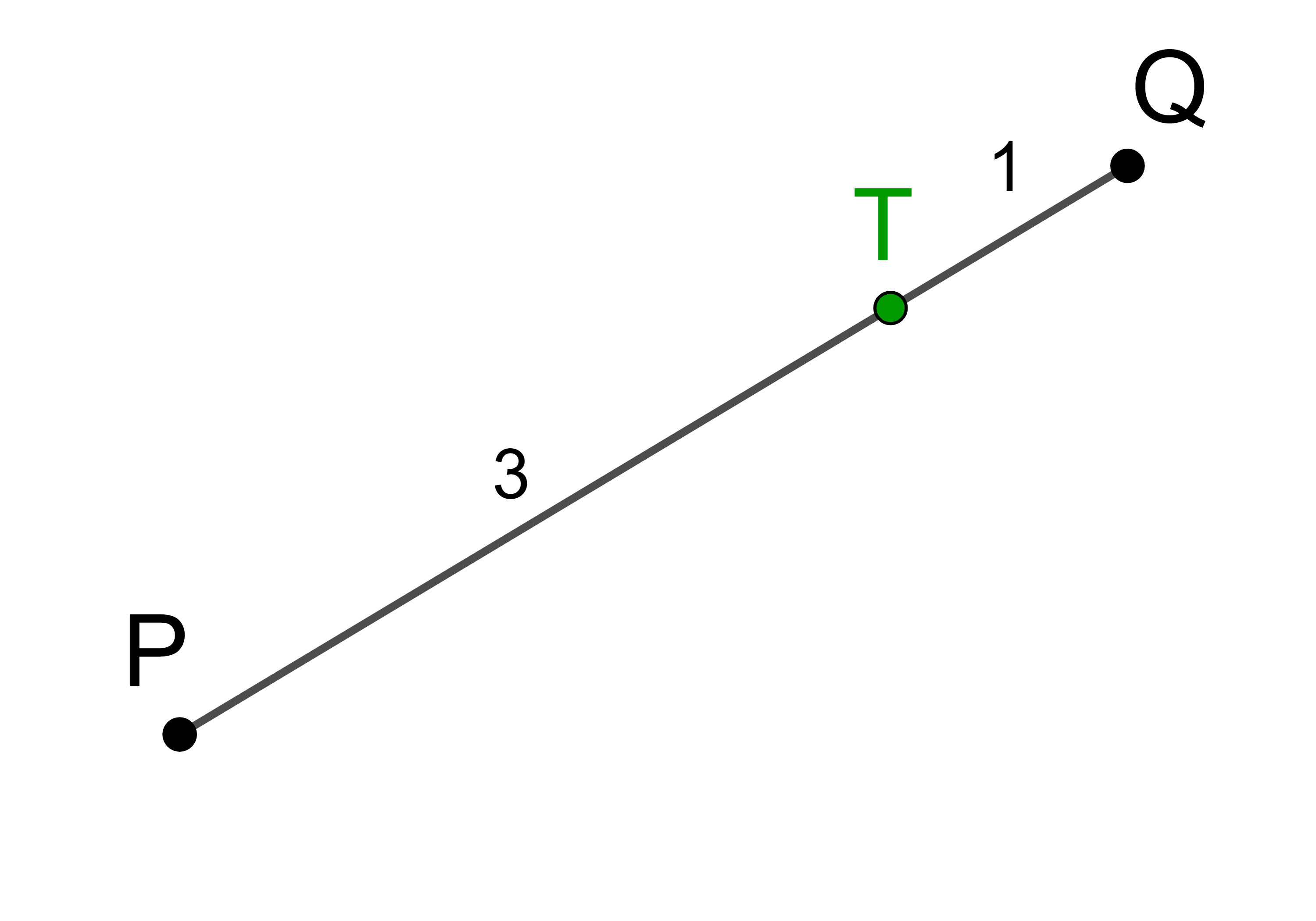
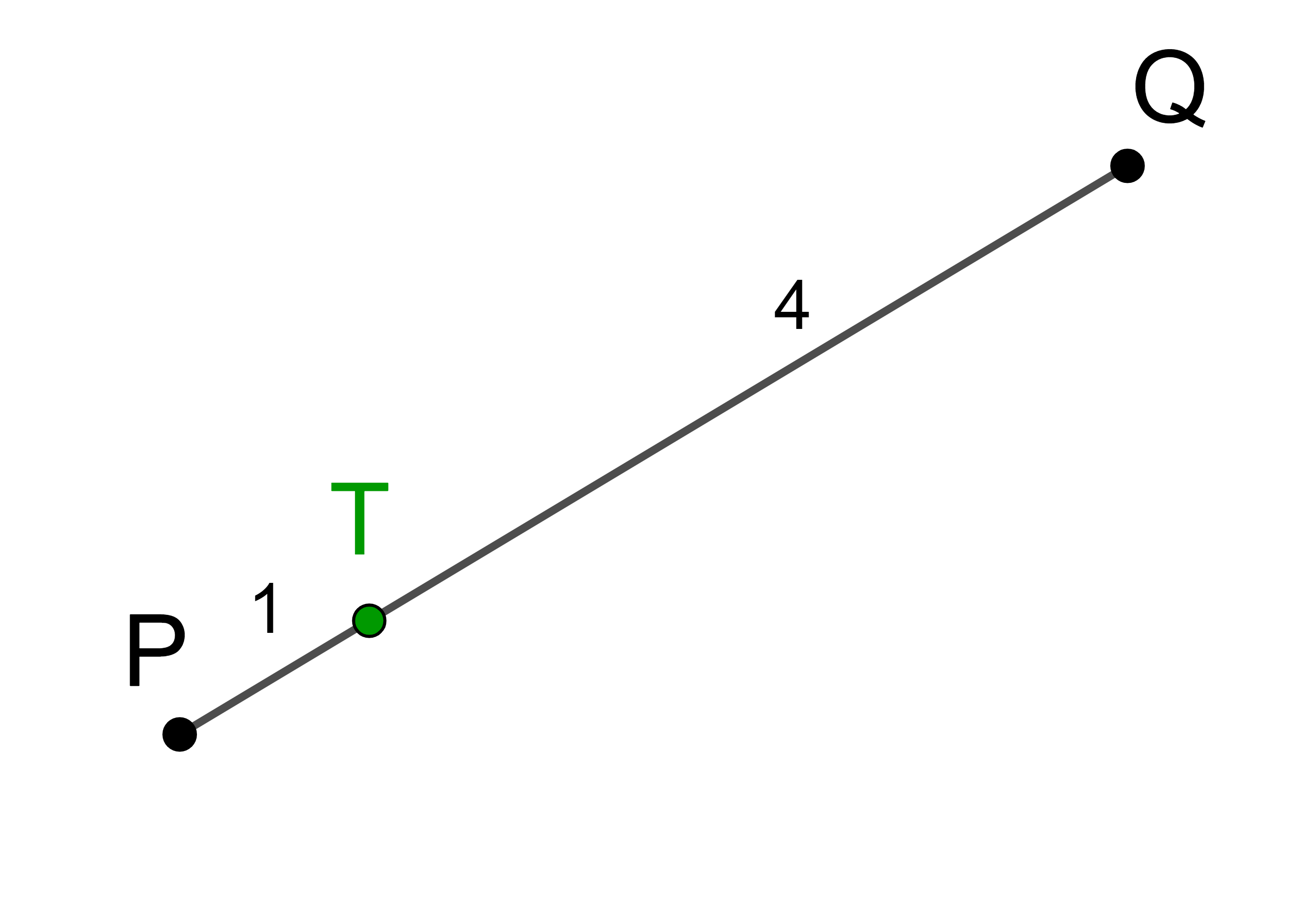
Der Punkt T teilt die Strecke PQ im Verhältnis 1 : 2.

Teilt man die Strecke PQ in 3 gleiche Teile, dann entfällt ein Teil auf die Strecke PT und zwei Teile entfallen auf die Strecke TQ.
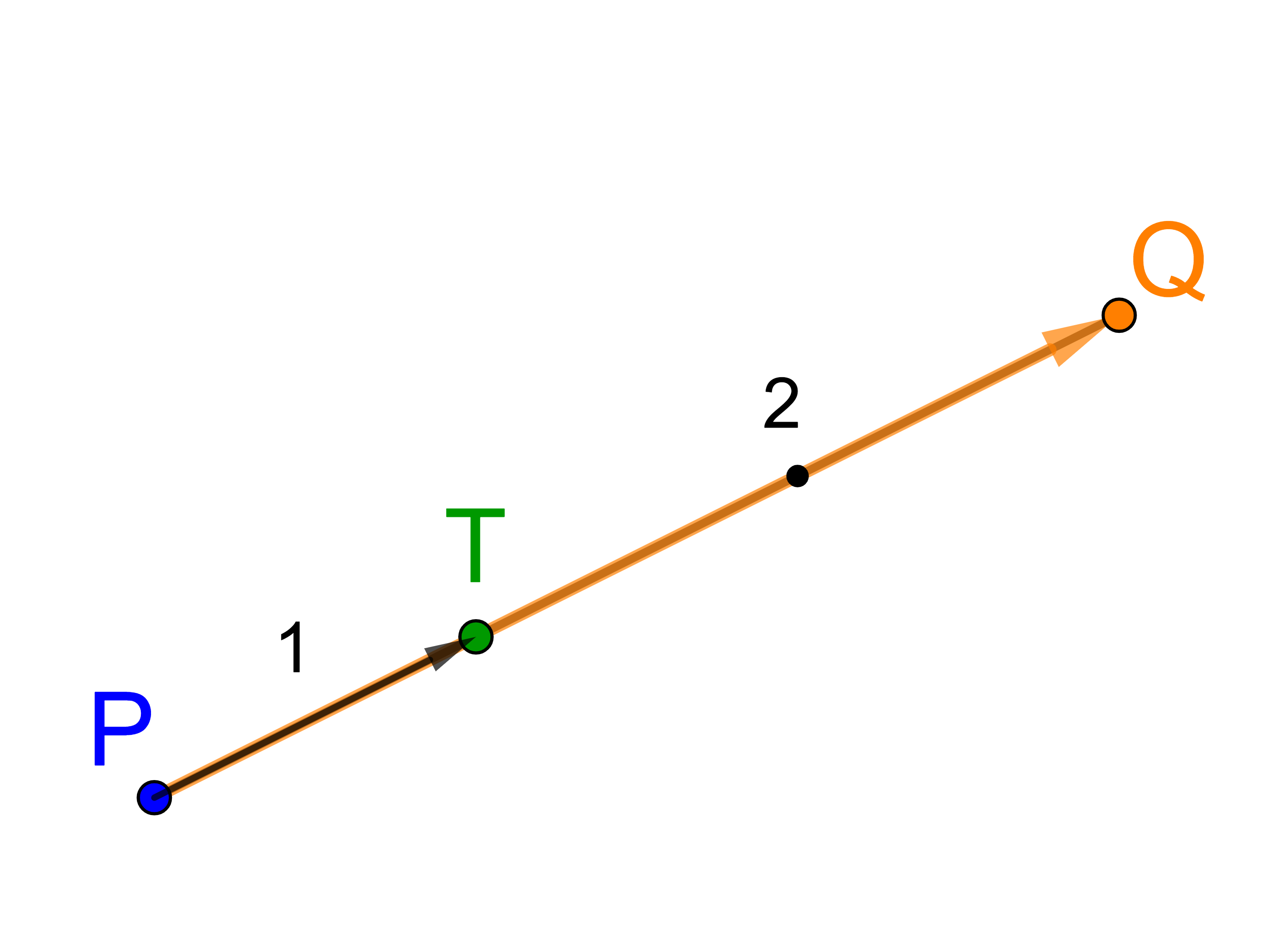
Die Strecke PT ist ein Drittel der Strecke PQ. Deshalb gilt:
⟶
OT
=
⟶
OP
+
1
3
⋅
⟶
PQ
=
(
-2
4
7
)
+
1
3
⋅
(
9
12
-15
)
=
(
-2
4
7
)
+
(
3
4
-5
)
=
(
1
8
2
)



T(1 | 8 | 2) ist der gesuchte Teilungspunkt der Strecke PQ.
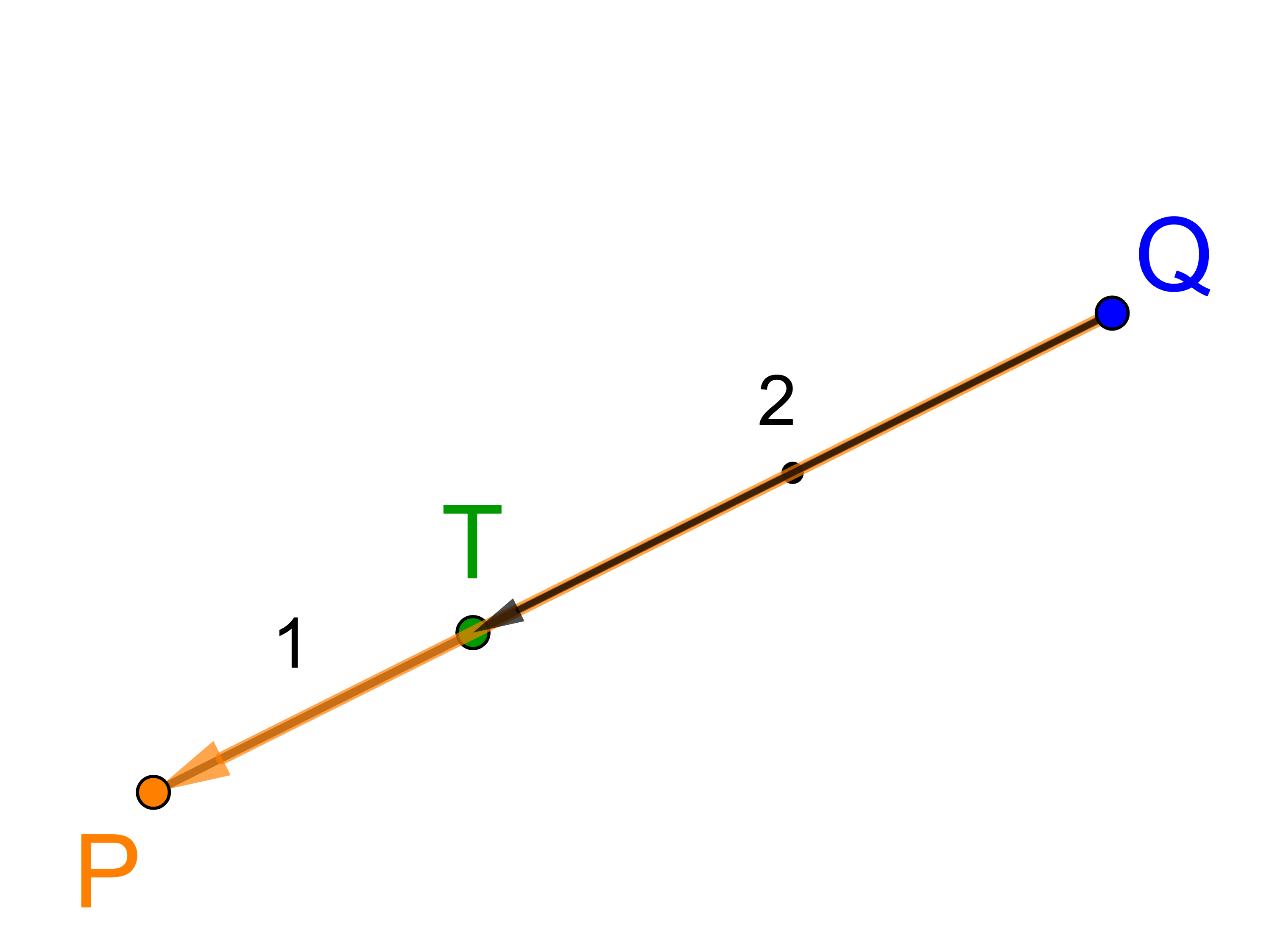
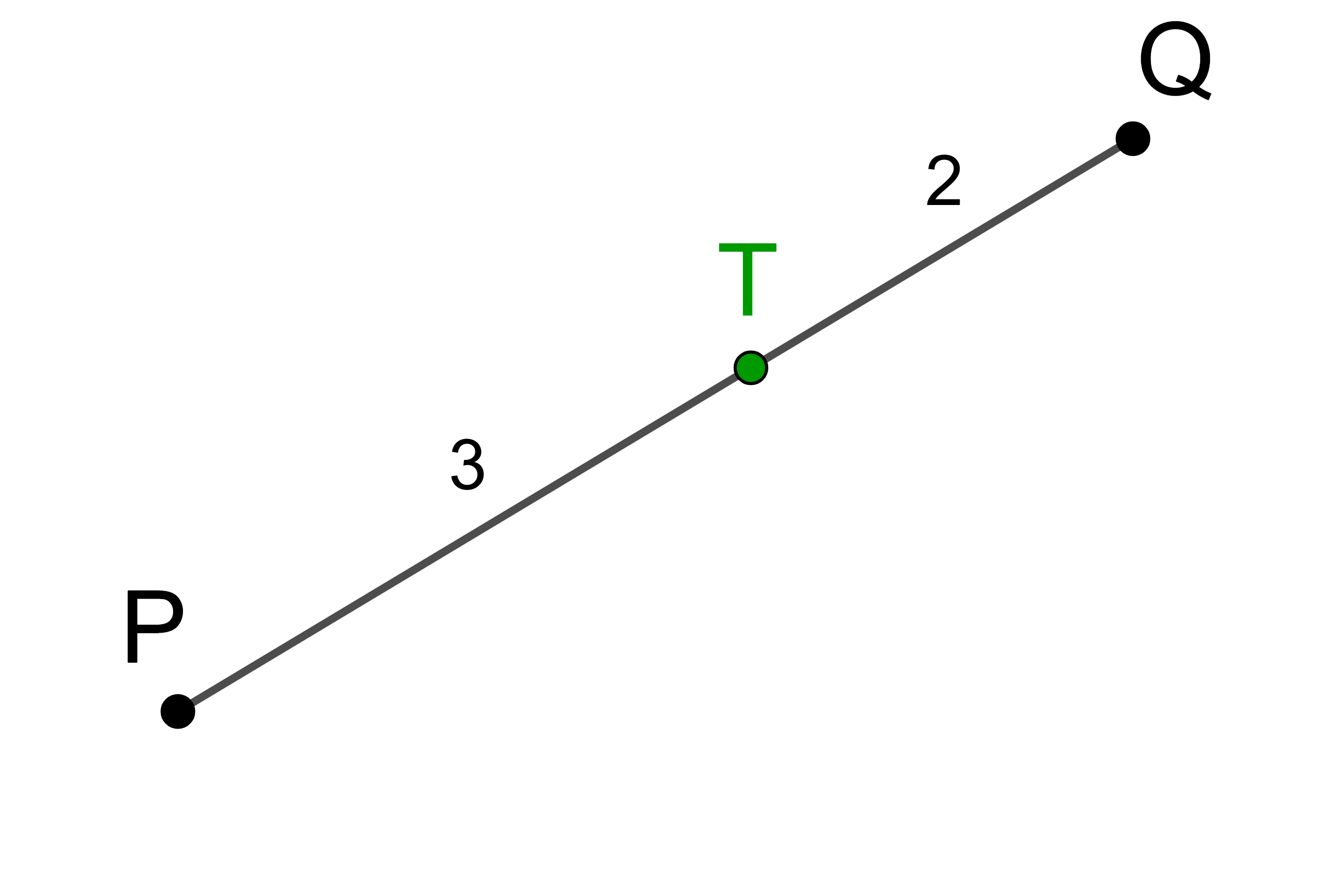
Die Koordinaten von T können auch mit Hilfe des Aufpunktes Q ermittelt werden. Die Strecke TQ ist zwei Drittel der Strecke PQ. Deshalb gilt:
⟶
OT
=
⟶
OQ
+
2
3
⋅
⟶
QP
=
(
7
16
-8
)
+
2
3
⋅
(
-9
-12
15
)
=
(
7
16
-8
)
+
(
-6
-8
10
)
=
(
1
8
2
)



T(1 | 8 | 2) ist der gesuchte Teilungspunkt der Strecke PQ.
Übung 1:
Gegeben ist ein Parallelogramm mit den Eckpunkten 
A(
-1
 | 
-2
)
 , 
B(
5
 | 
-6
)
 , 
C(
3
 | 
-2
)
 und 
D(
-3
 | 
2
)
 .
Berechnen Sie die Koordinaten des Mittelpunktes M der Seite AB des Parallelogramms mit Hilfe von Ortsvektoren.
⟶
   =   
⟶
   +   
1
2
⋅  
⟶
   =   
(

)
   +   
1
2
⋅  
(

)
   =   
(

)
 ( 
 | 
 ) 
  ist der gesuchte Punkt.
Kontrolle
Lösung
Bei wiederholtem Drücken des Lösungsbuttons werden weitere Lösungsmöglichkeiten angezeigt.
Neue Aufgabe
Übung 2:
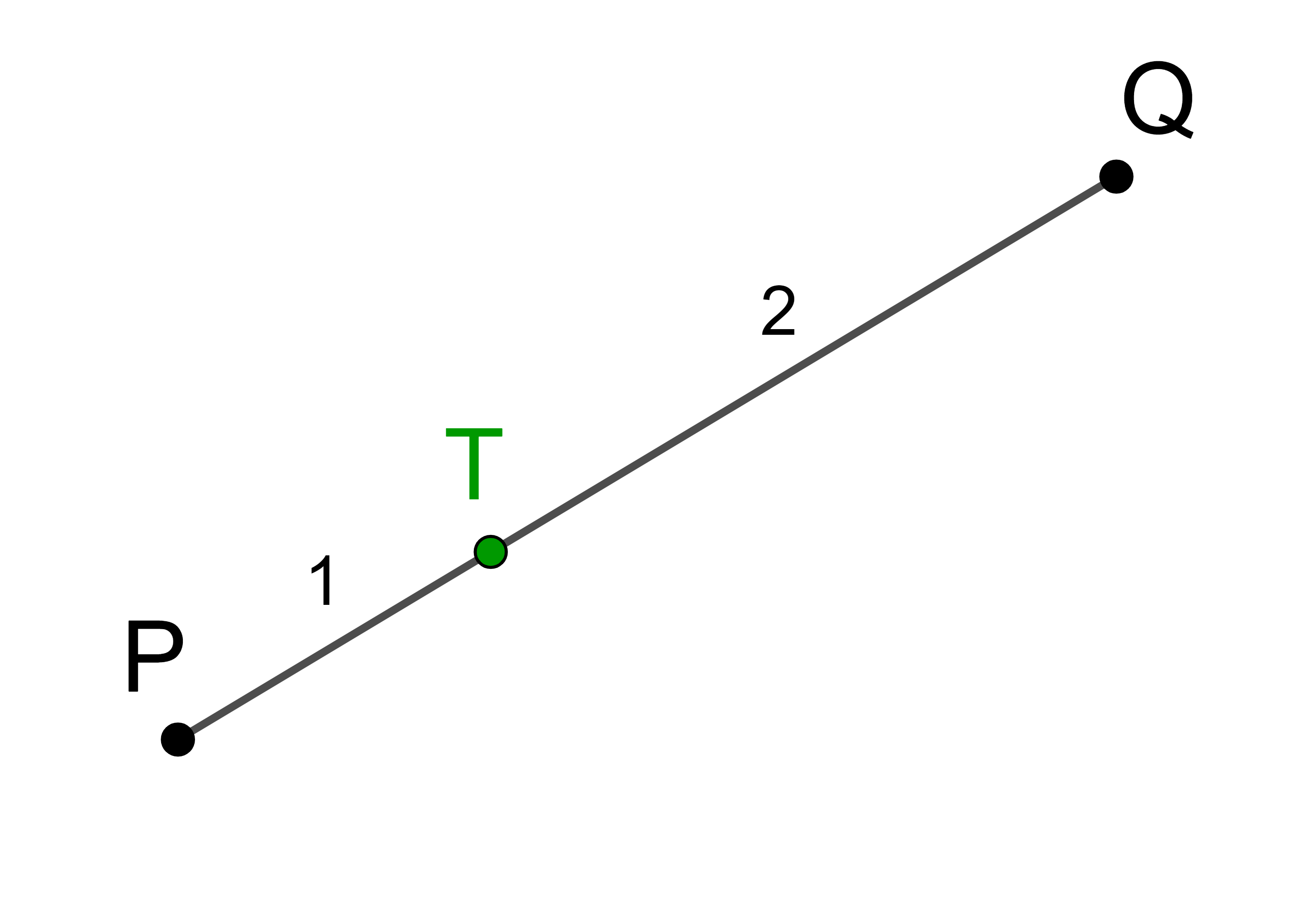
Gegeben sind die Punkte 
P(
2
 | 
-3
 | 
5
)
 und 
Q(
-7
 | 
3
 | 
20
)
 im Raum.


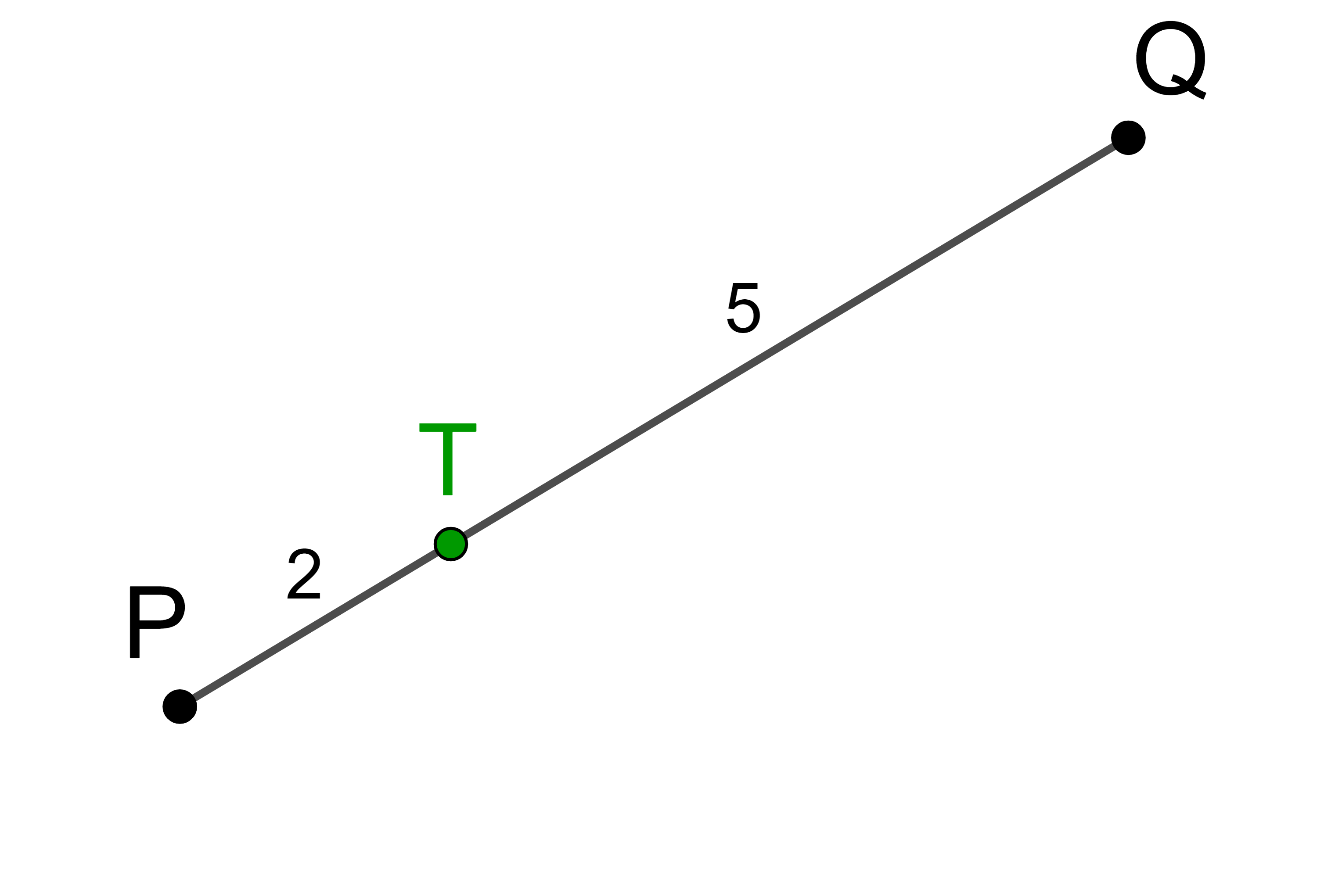
Der Punkt T teilt die Strecke PQ im Verhältnis 
1
 : 
2
 . 



Berechnen Sie die Koordinaten von T mit Hilfe von Ortsvektoren.
⟶
  =  
⟶
  +  
⋅  
⟶
  =  
(

)
  +  
⋅  
(

)
  =  
(

)
  +  
(

)
  =  
(

)
T ( 
 | 
 | 
 ) 
  ist der gesuchte Teilungspunkt.
Kontrolle
Lösung
Bei nochmaligem Drücken des Lösungsbuttons wird eine weitere Lösungsmöglichkeit angezeigt.
Neue Aufgabe
4.1. ←