11. Graphische Darstellung von Binomialverteilungen und Erwartungswert
← Kapitelübersicht
Mit Hilfe der Ergebnisse und Informationen aus den Kapiteln 9 und 10 kann eine Binomialverteilung zur Glücksspielaufgabe aus Kapitel 1 mit n = 5 und p = 0,25 erstellt werden.
Die Wahrscheinlichkeiten für die einzelnen Ergebnisse der Zufallsgröße X (= Anzahl der Treffer innerhalb einer Bernoulli-Kette) wurden auf die vierte Nachkommastelle gerundet.
Die Wahrscheinlichkeiten für die einzelnen Ergebnisse der Zufallsgröße X (= Anzahl der Treffer innerhalb einer Bernoulli-Kette) wurden auf die vierte Nachkommastelle gerundet.
| k | 0 | 1 | 2 | 3 | 4 | 5 |
| P(X = k) | 0,2373 | 0,3955 | 0,2637 | 0,0879 | 0,0146 | 0,001 |
Die Binomialverteilung kann durch ein Säulendiagramm graphisch dargestellt werden. Die möglichen Ergebnisse der Zufallsgröße X befinden sich auf der x-Achse. Die Höhe der Säule - ablesbar an der y-Achse - gibt an, mit welcher Wahrscheinlichkeit das jeweilige Ergebnis eintritt.
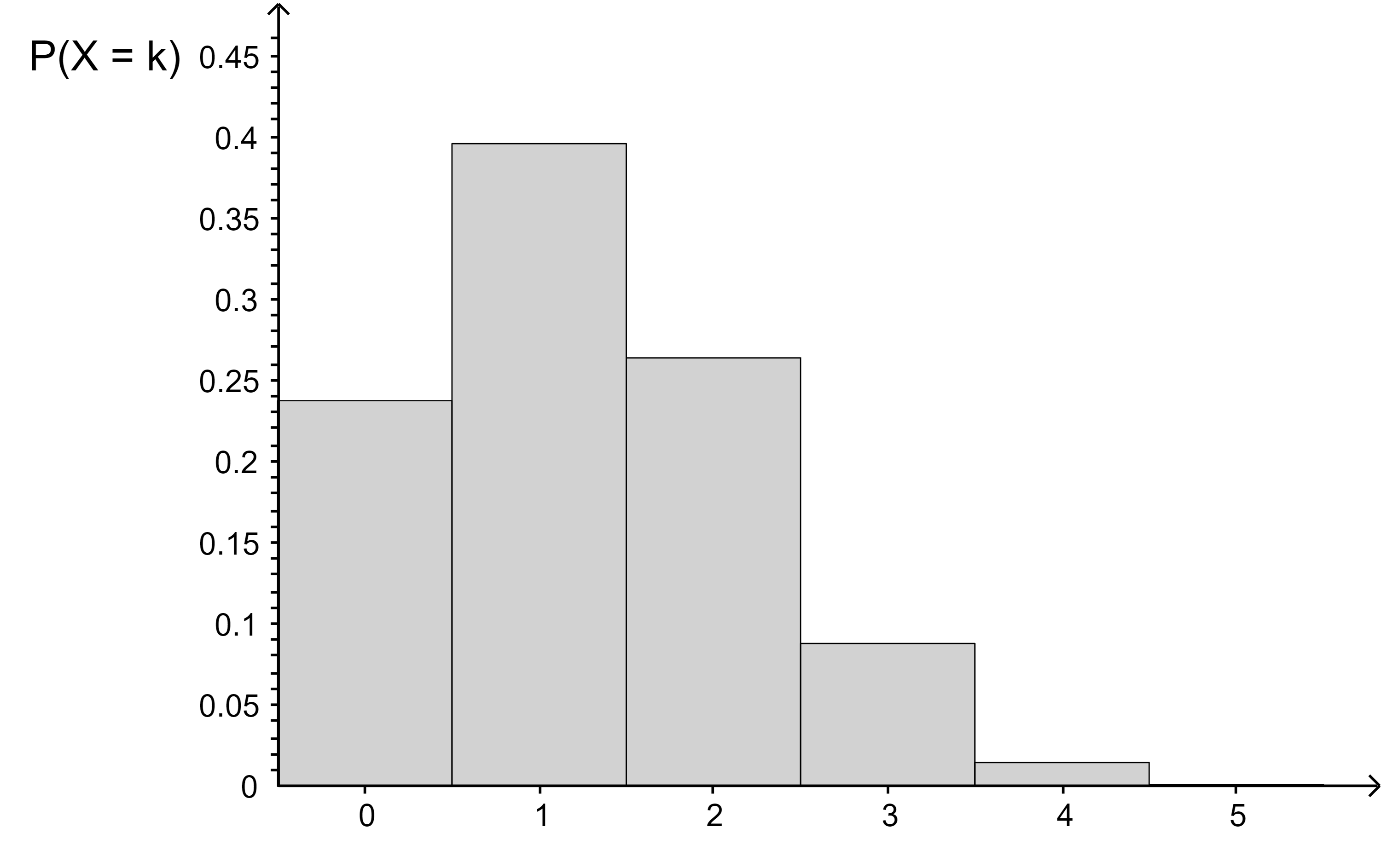
Angenommen, man führt das Glücksspiel aus Kapitel 1 sehr oft durch (z.B. 1000mal), notiert jeweils die eingetretene Trefferzahl und bildet anschließend den Mittelwert aus allen Trefferzahlen, dann liegt dieser statistische Wert in der Nähe des sogenannten Erwartungswertes der Zufallsgröße X.
Für eine Bernoulli-Kette mit der Länge n und der Trefferwahrscheinlichkeit p gilt:
Der Erwartungswert μ der Zufallsgröße X wird berechnet mit der Formel: μ = n ⋅ p .
Er gibt eine Prognose ab für den Mittelwert aller eingetretenen Trefferzahlen bei einer hohen Anzahl von Wiederholungen des mehrstufigen Zufallsversuchs.
Der Erwartungswert μ der Zufallsgröße X wird berechnet mit der Formel: μ = n ⋅ p .
Er gibt eine Prognose ab für den Mittelwert aller eingetretenen Trefferzahlen bei einer hohen Anzahl von Wiederholungen des mehrstufigen Zufallsversuchs.
Für das Glücksspiel aus Kapitel 1 erhält man als Erwartungswert: μ = 5 ⋅ 0,25 = 1,25.
Trägt man den Erwartungswert auf der x-Achse des Säulendiagramms ein, dann liegt er in der Nähe der Trefferzahl mit der höchsten Wahrscheinlichkeit.
Trägt man den Erwartungswert auf der x-Achse des Säulendiagramms ein, dann liegt er in der Nähe der Trefferzahl mit der höchsten Wahrscheinlichkeit.
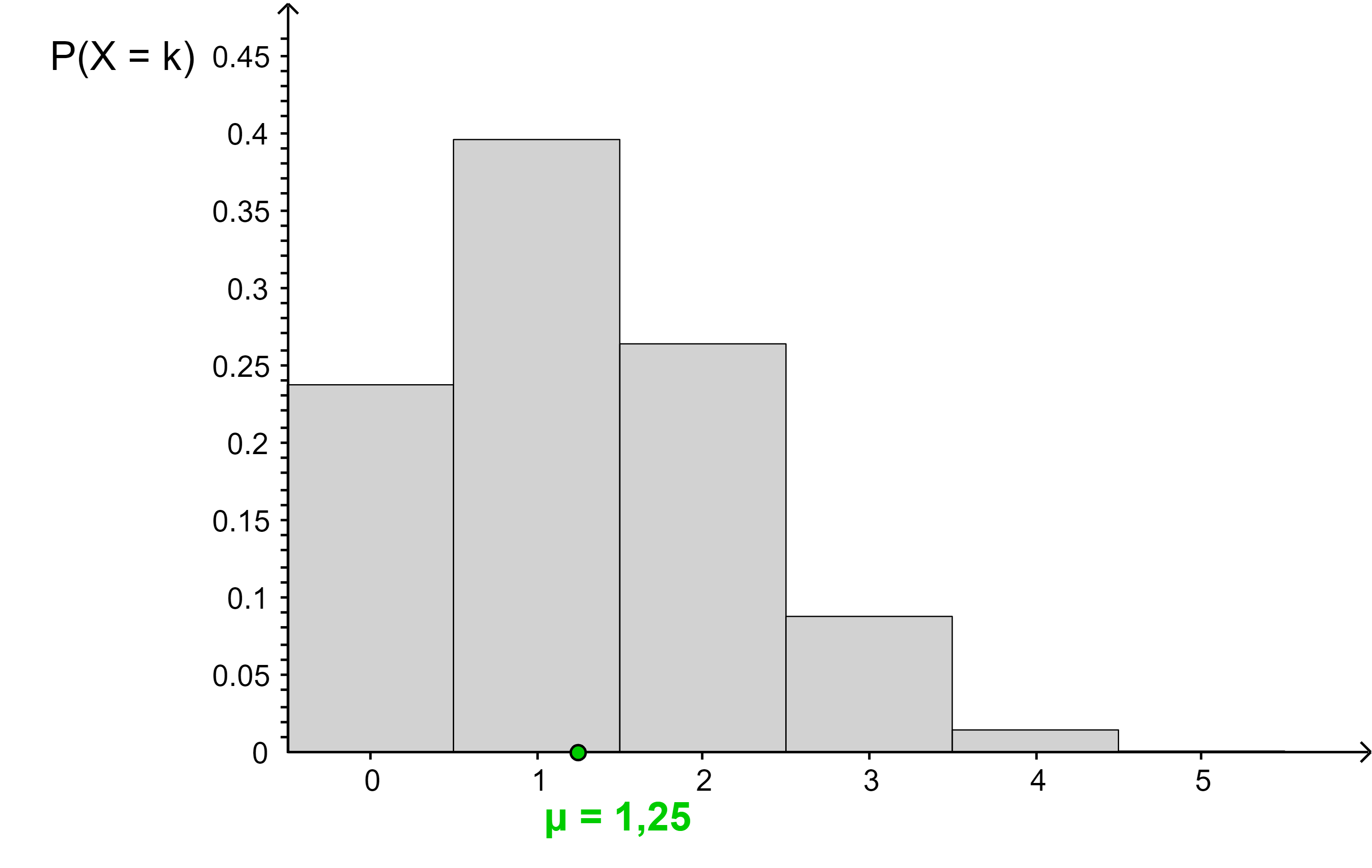
Übungsaufgaben:
Die nachfolgenden Diagramme stellen jeweils eine Binomialverteilung dar. Entscheiden Sie, welches der drei angegebenen Wertepaare für n und p zum Diagramm passt.
Aufgabe 1:
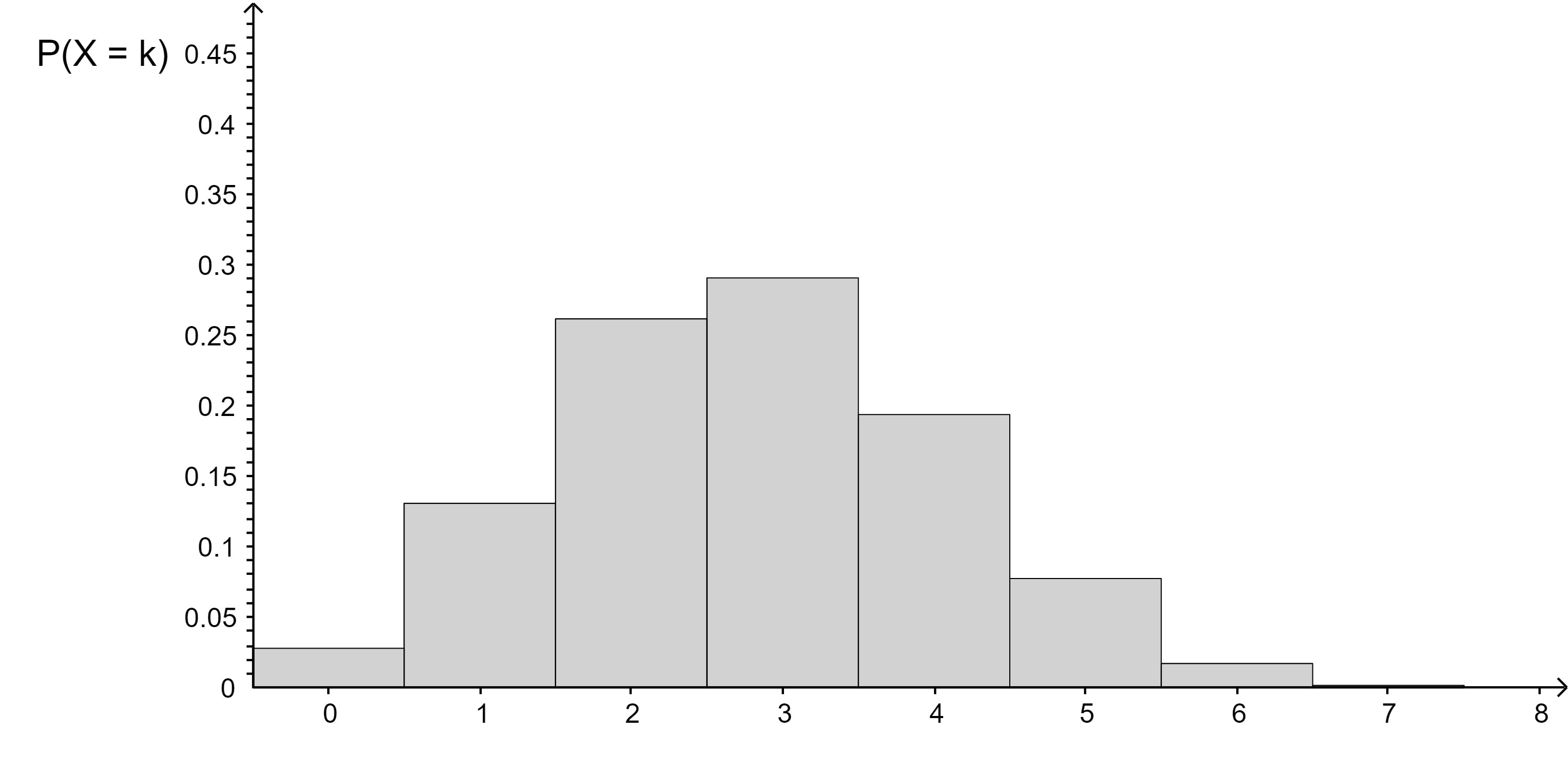
n = 7 , p = 0,2
n = 5 , p = 0,6
n = 7 , p = 0,4
Aufgabe 2:
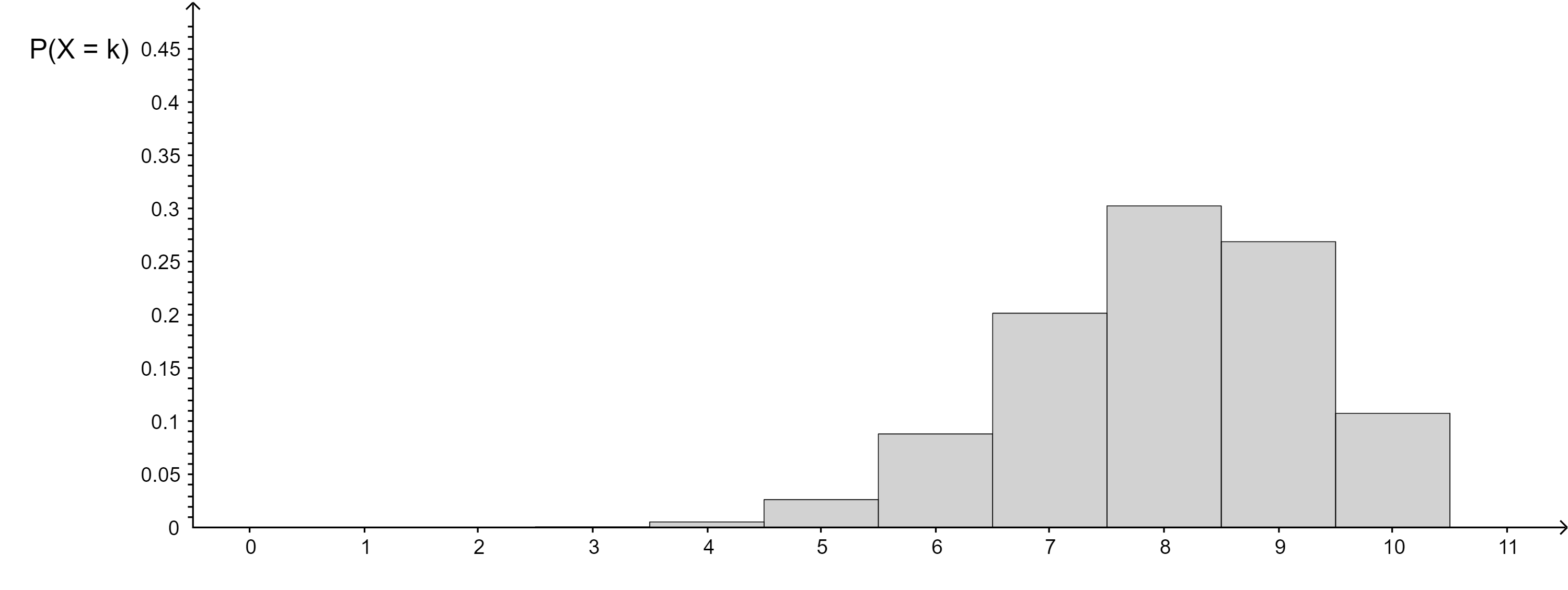
n = 9 , p = 0,9
n = 10 , p = 0,8
n = 10 , p = 0,7
Aufgabe 3:
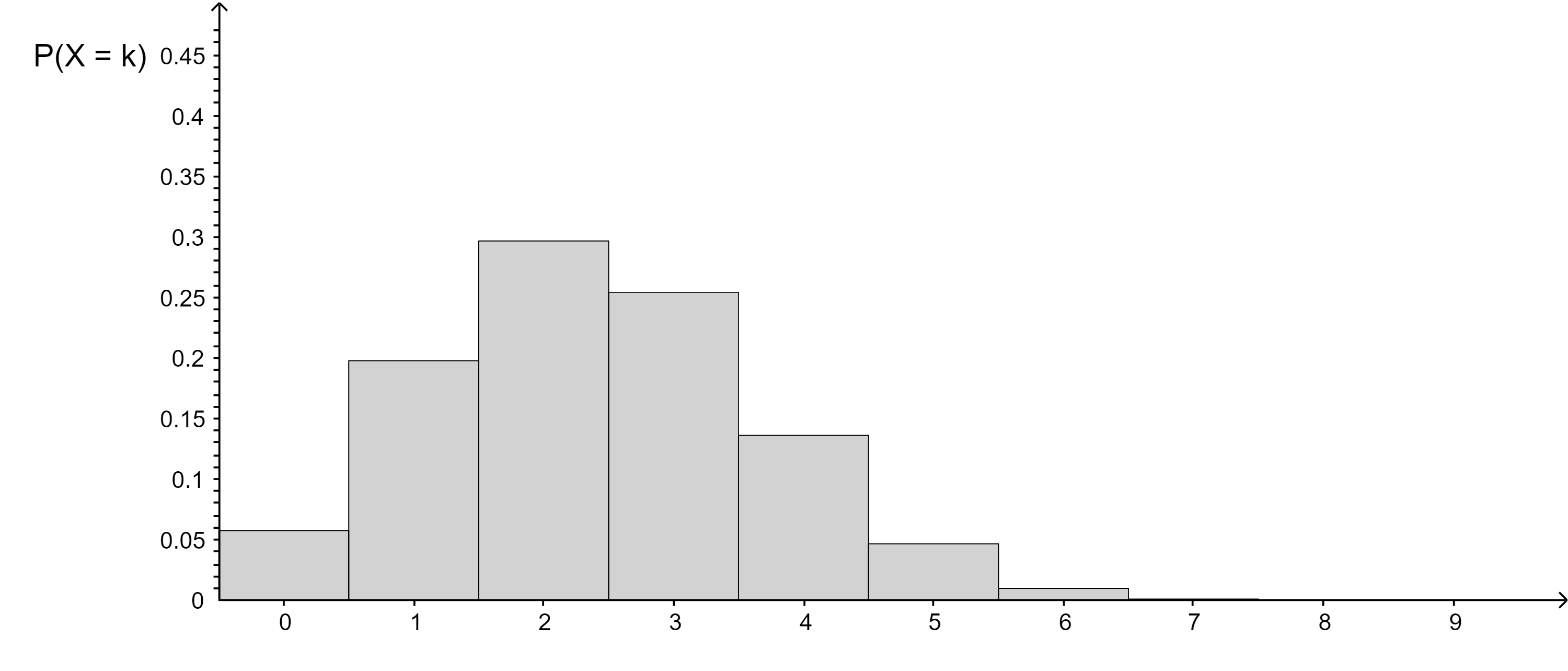
n = 8 , p = 0,5
n = 9 , p = 0,1
n = 8 , p = 0,3
Aufgabe 4:
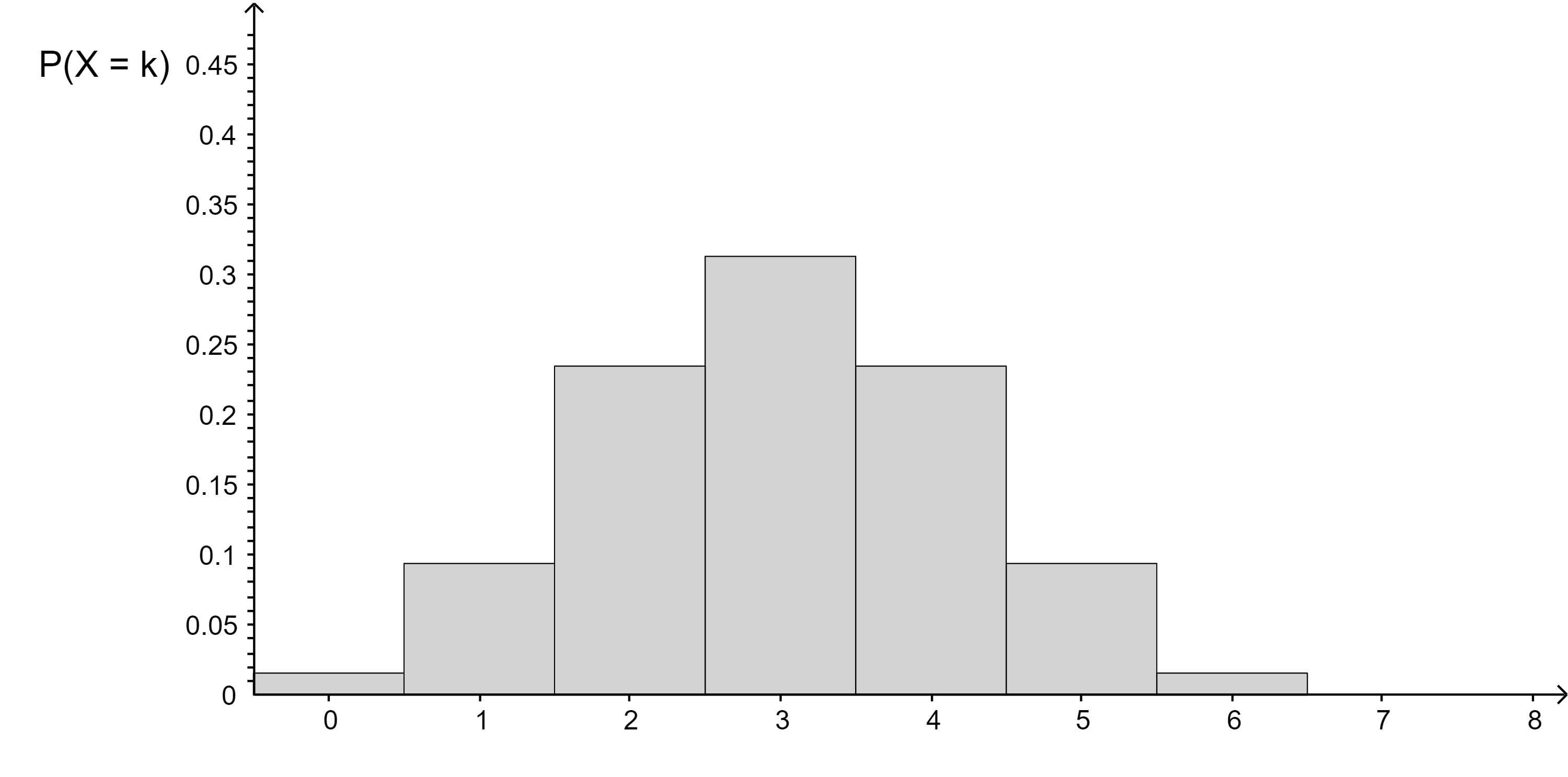
n = 6 , p = 0,5
n = 7 , p = 0,6
n = 4 , p = 0,8