⌂ Mathe-Training für die Oberstufe - Interaktive Lernprogramme

Berechnung von Flächeninhalten mit Hilfe von Integralen

← Themenübersicht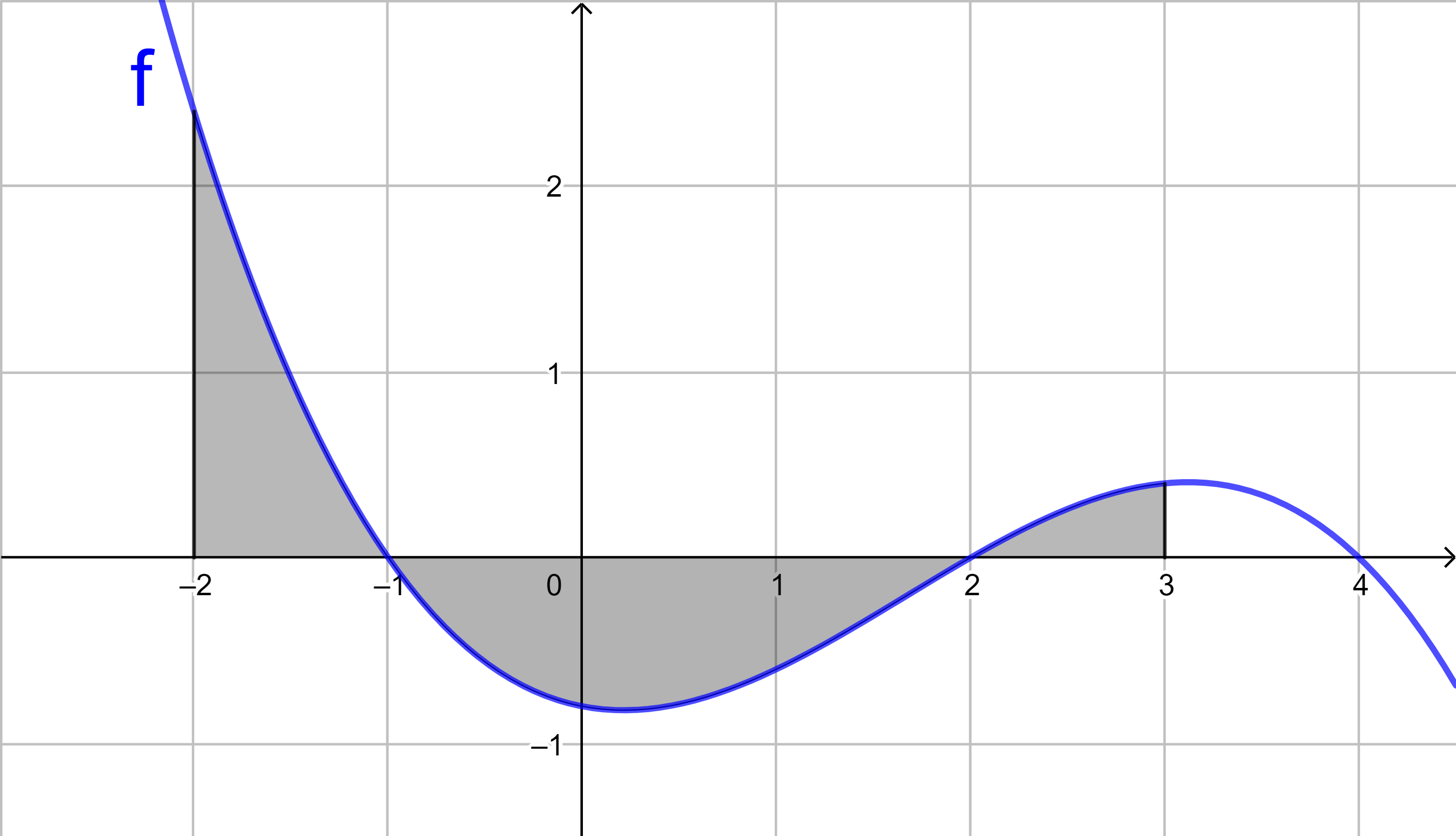
Der Inhalt einer Fläche, die von einem Funktionsgraphen, der x-Achse und zur y-Achse parallelen Geraden begrenzt wird, kann mit Hilfe von Integralen berechnet werden. Die Vorgehensweise wird an zwei Beispielen demonstriert und kann anschließend mit weiteren Aufgaben geübt werden.
Beispiel 1:
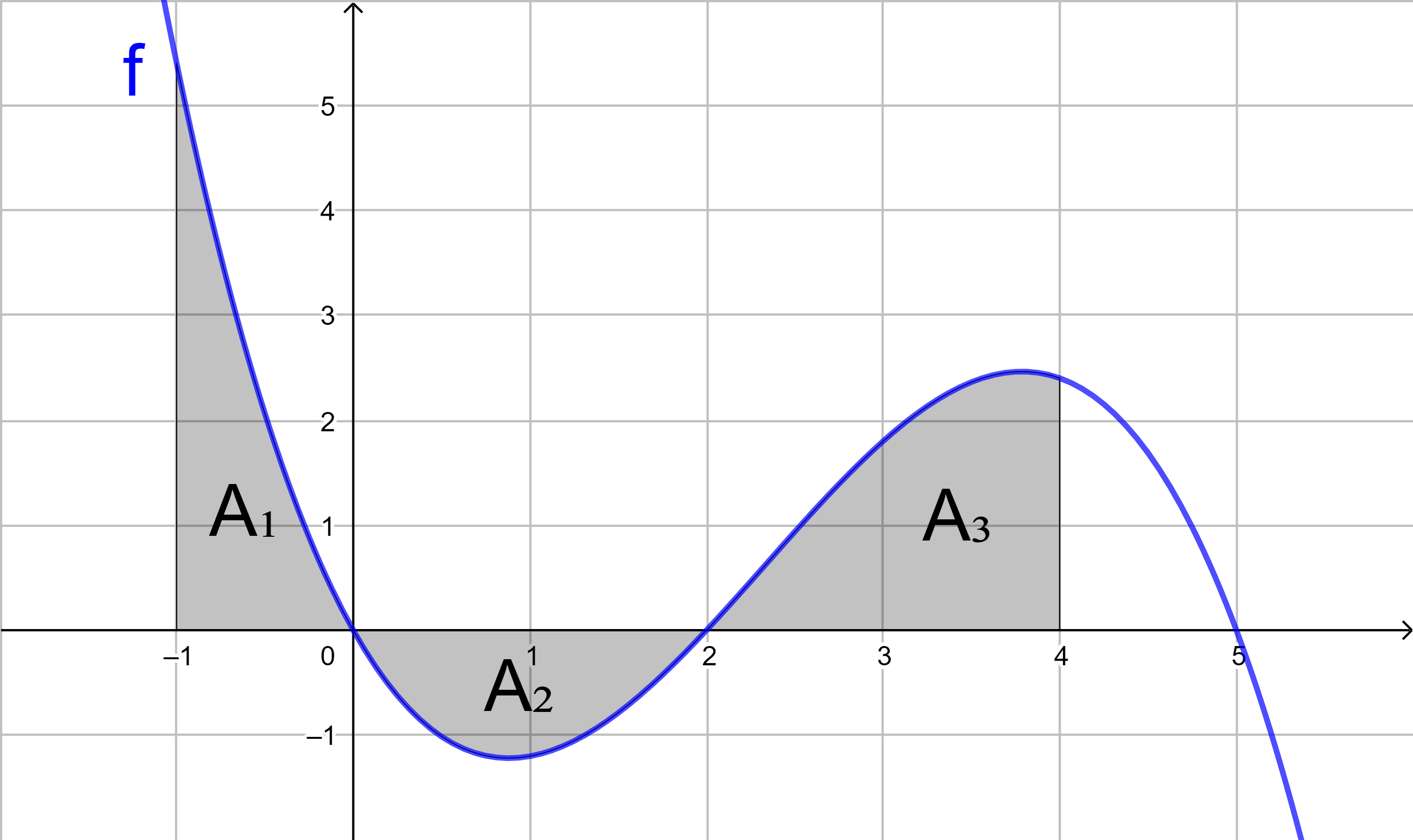
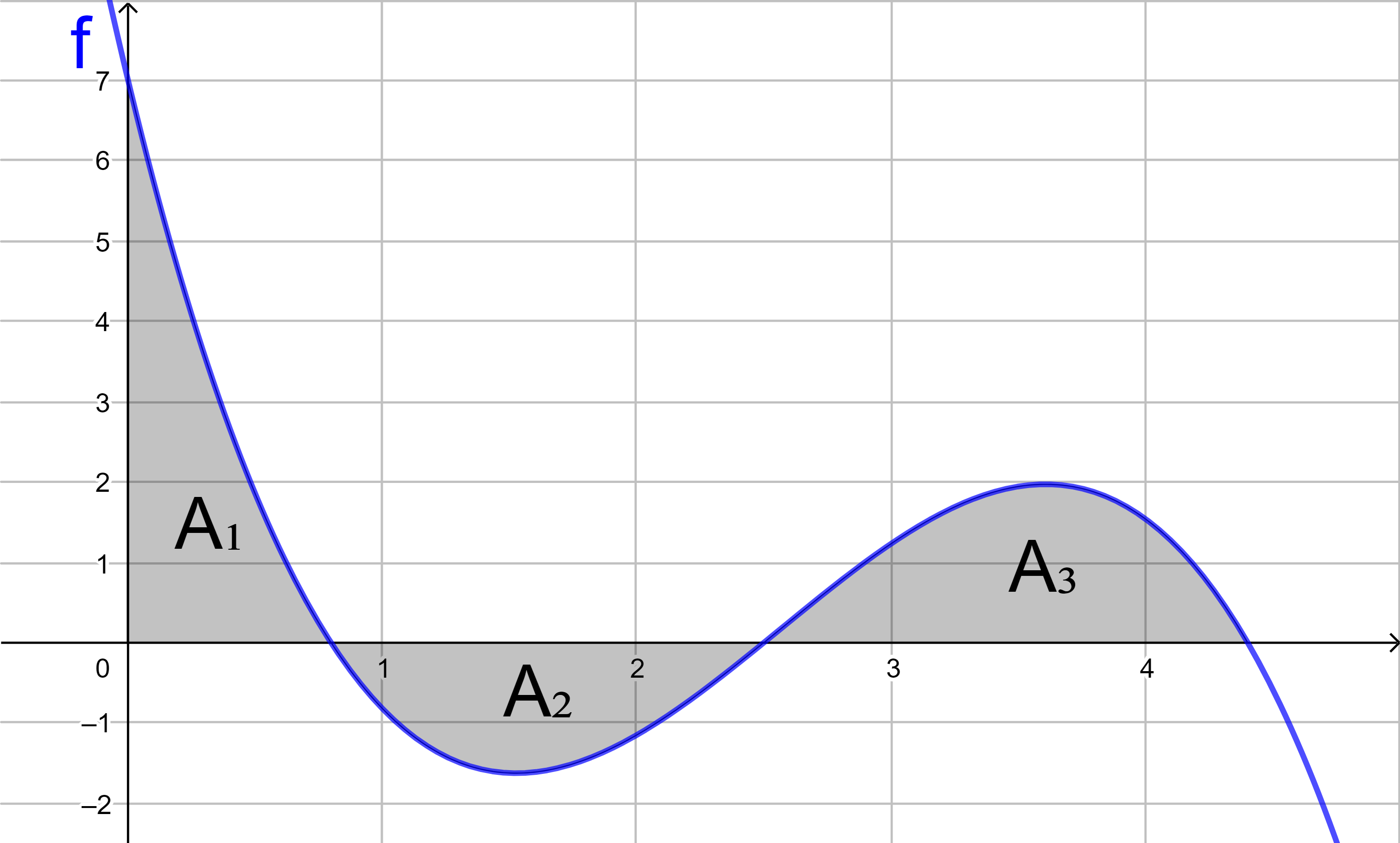
Bestimmen Sie für die Funktion f mit
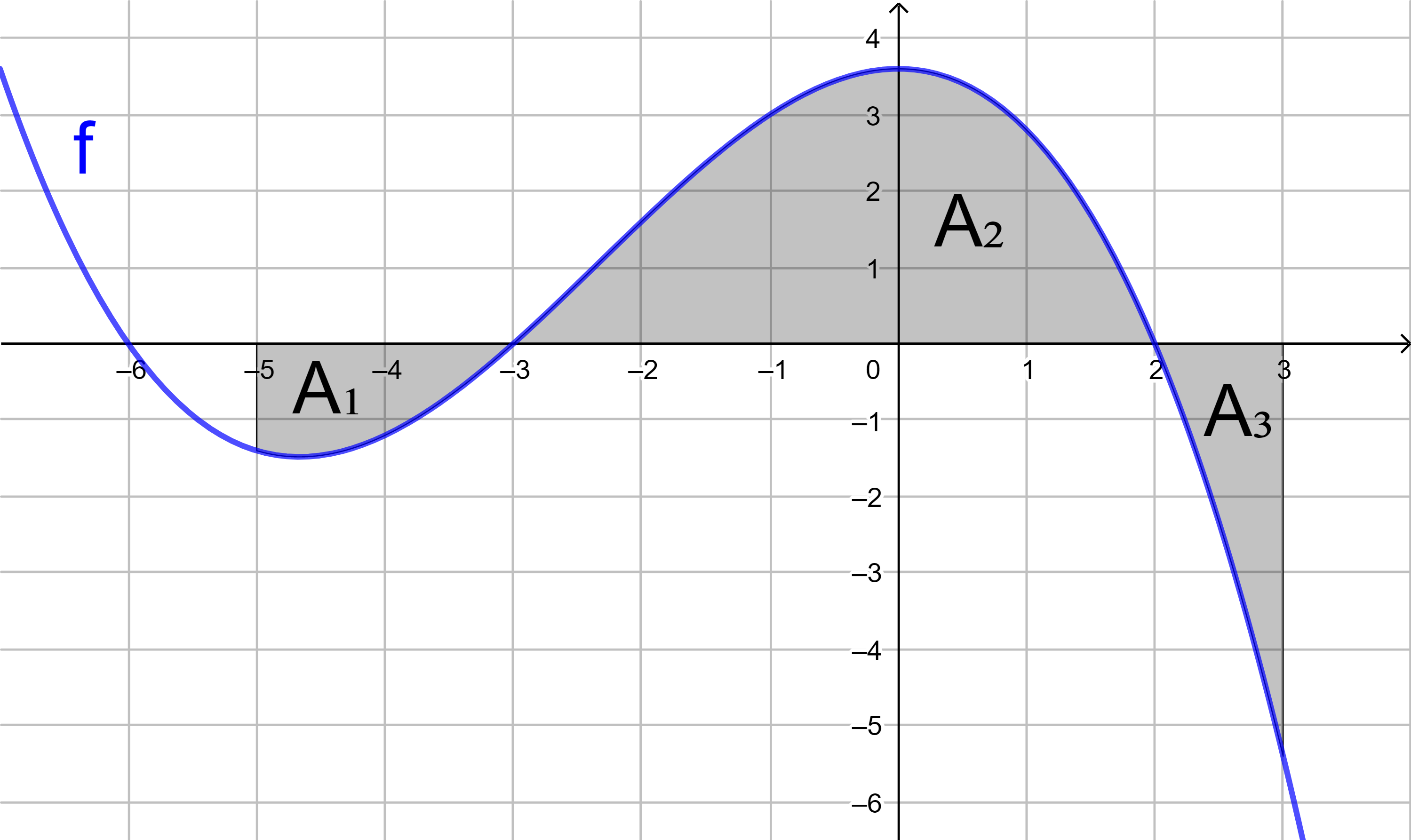
f(x) = -0,1x3 + 0,5x2 - 0,2x - 0,8
mit Hilfe von Integralen den Flächeninhalt
der grau markierten Fläche.
Mit Integralen werden orientierte Flächeninhalte berechnet (siehe Kapitel 2). Liegt eine Fläche oberhalb der x‑Achse, ist ihr orientierter Flächeninhalt positiv, liegt sie unterhalb der x‑Achse, ist der orientierte Flächeninhalt negativ. Der Inhalt der grau markierten Fläche kann nicht mit einem einzigen Integral berechnet werden. Man benötigt für jedes Teilstück ein eigenes Integral.
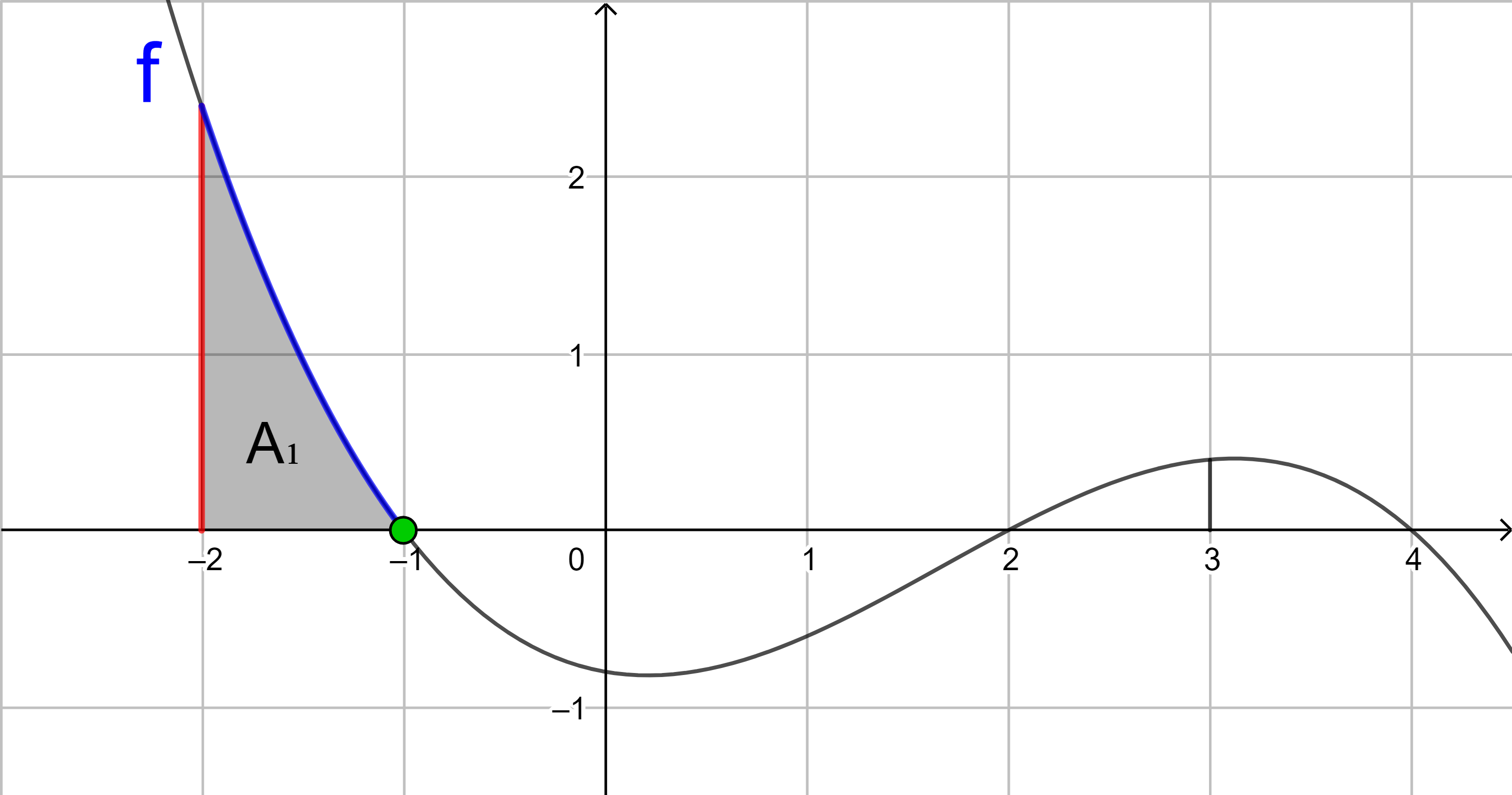
1. Flächenstück:
 -1
 ∫
f(x)
dx
-2
  =  1,042



  A1  =  1,042  (FE = Flächeneinheiten)
Der Wert des Integrals ist positiv, da die Fläche oberhalb der x‑Achse liegt. Er entspricht dem Flächeninhalt A1.
Der Integralwert kann mit dem GTR oder dem Hauptsatz der Differenzial- und Integralrechnung ermittelt werden.
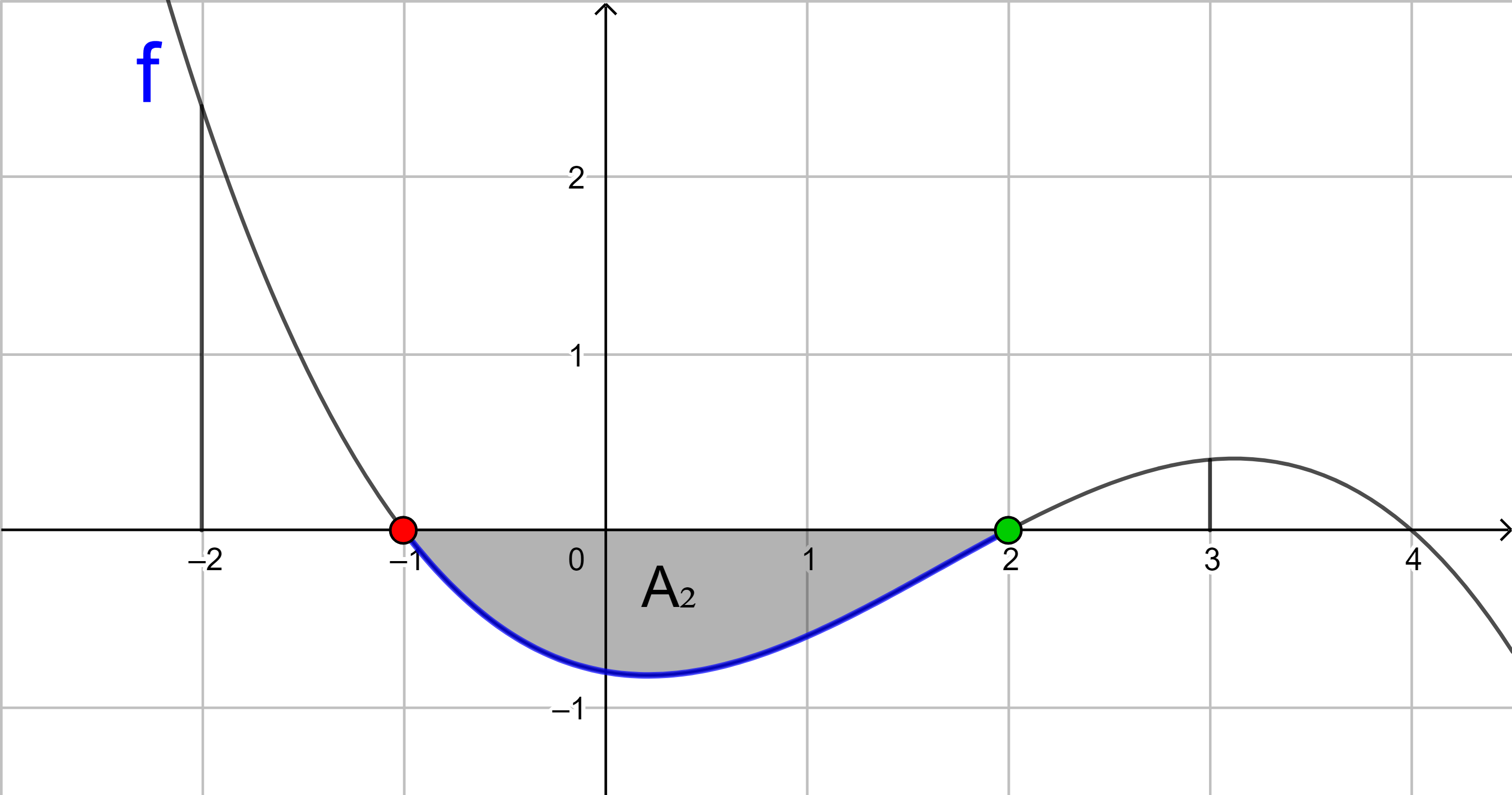
2. Flächenstück:
 2
 ∫
f(x)
dx
-1
  =  -1,575



  A2  =  |-1,575|  =  1,575  (FE)
Der Wert des Integrals ist negativ, da die Fläche unterhalb der x‑Achse liegt. Der Flächeninhalt A2 entspricht dem Betrag des Integralwertes.
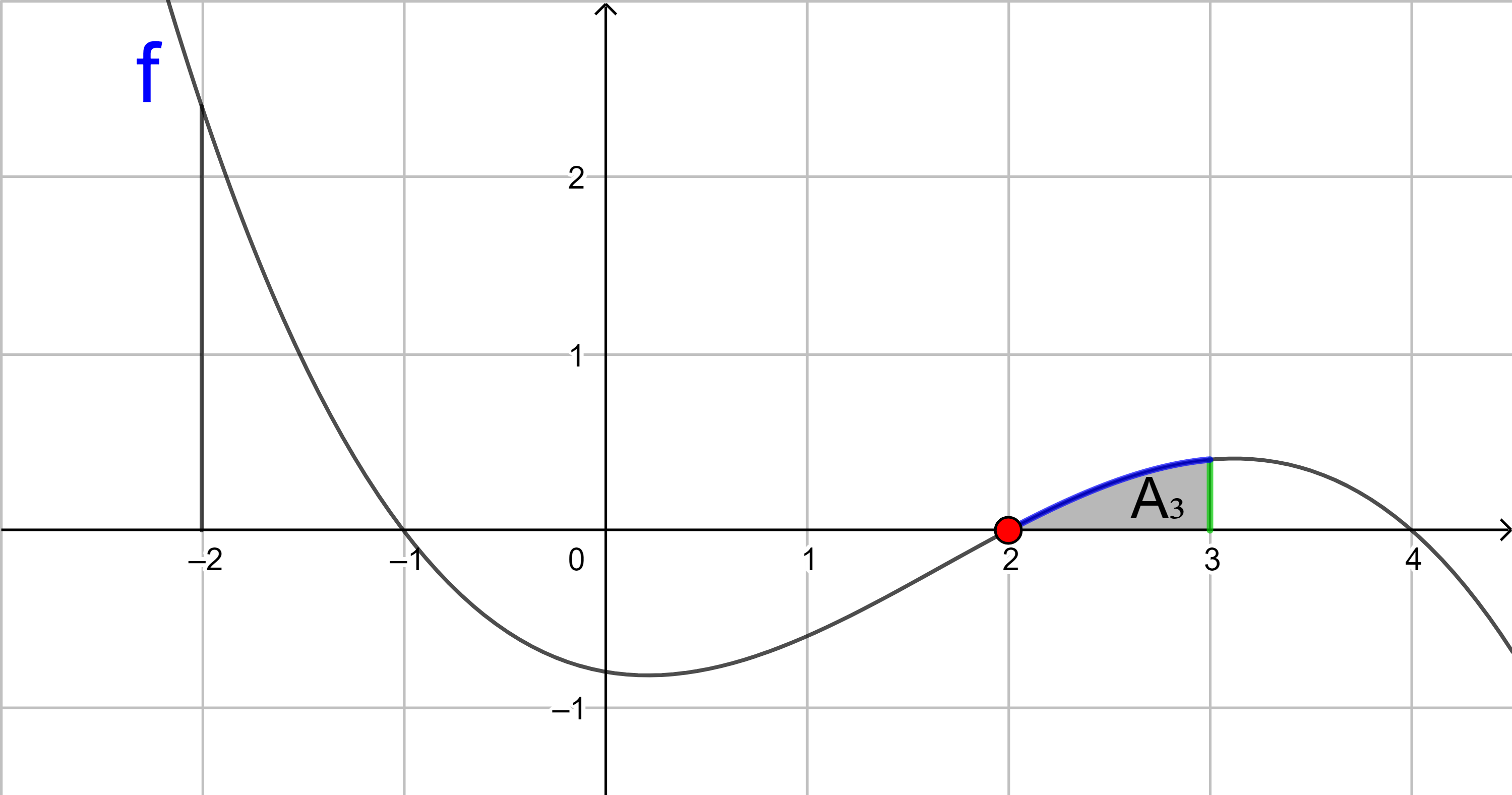
3. Flächenstück:
 3
 ∫
f(x)
dx
2
  =  0,242



  A3  =  0,242  (FE)
Der Wert des Integrals ist positiv, da die Fläche oberhalb der x‑Achse liegt. Er entspricht dem Flächeninhalt A3.
Berechnung des Flächeninhalts A der gesamten Fläche:

A  =  A1  +  A2  +  A3  =  1,042  +  1,575  +  0,242  =  2,859  (FE)
Sie können die Berechnung von Flächeninhalten mit Hilfe von Integralen jetzt üben. Wählen Sie weitere Aufgaben durch Anklicken aus.
Aufgabe:
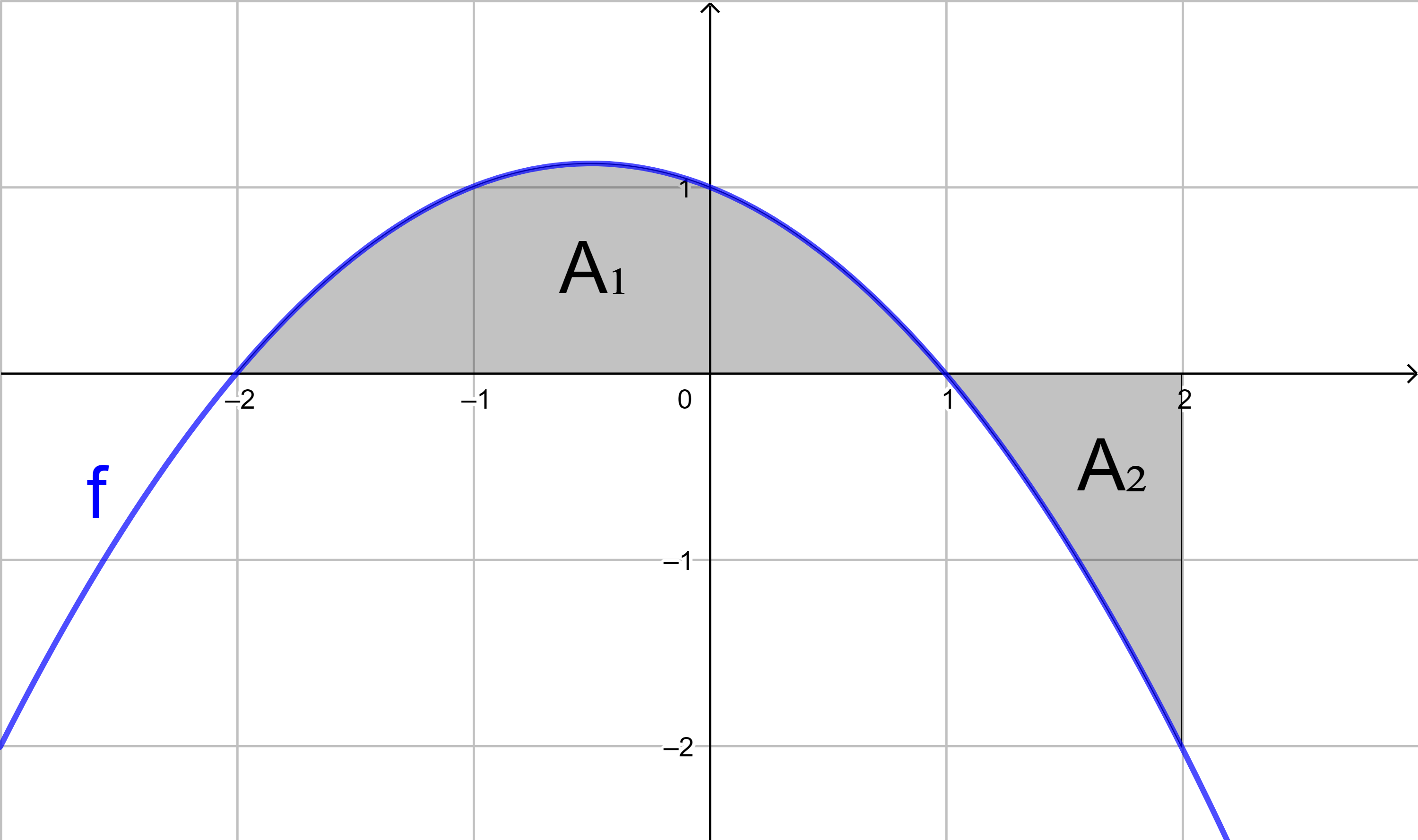
Aufgabe:
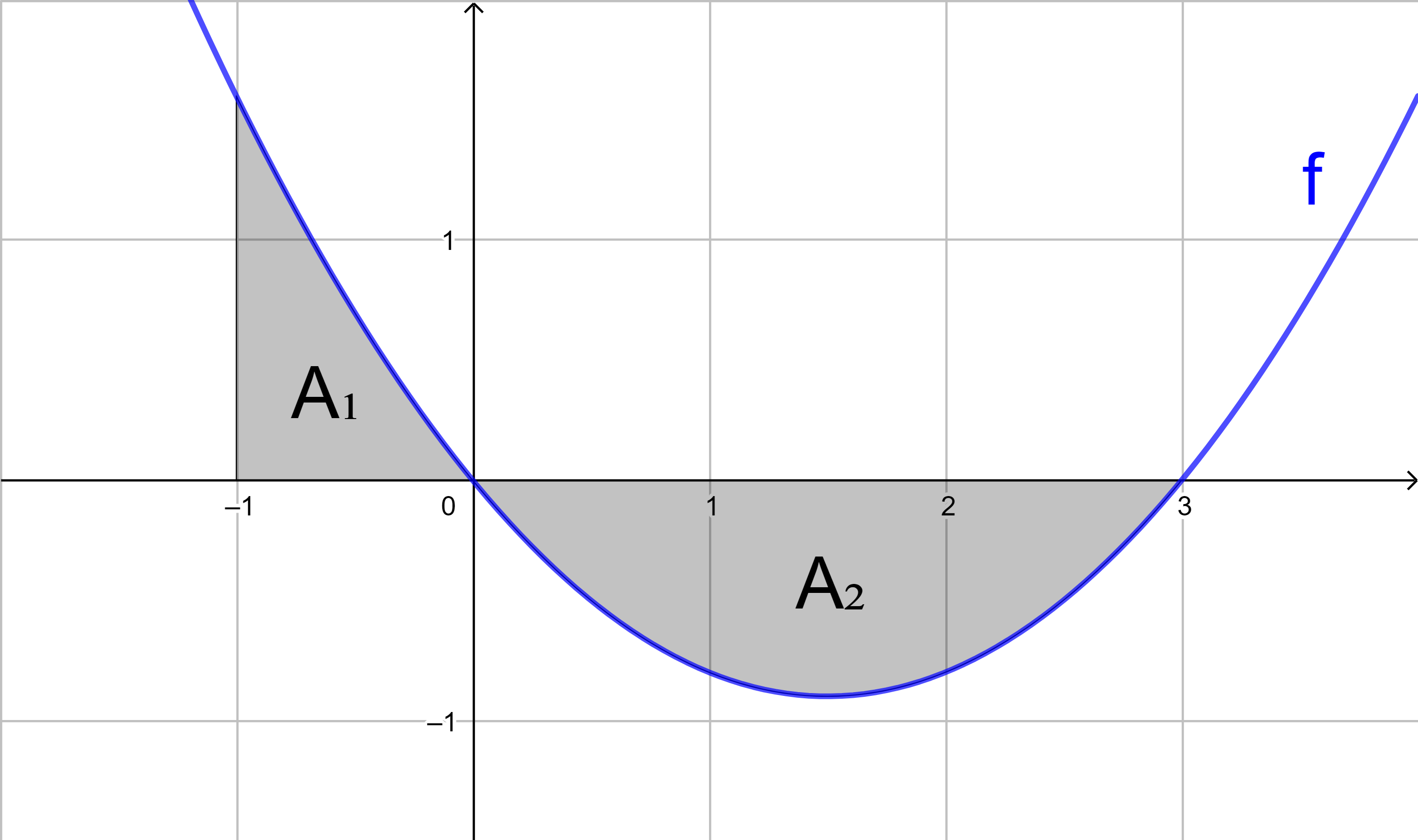
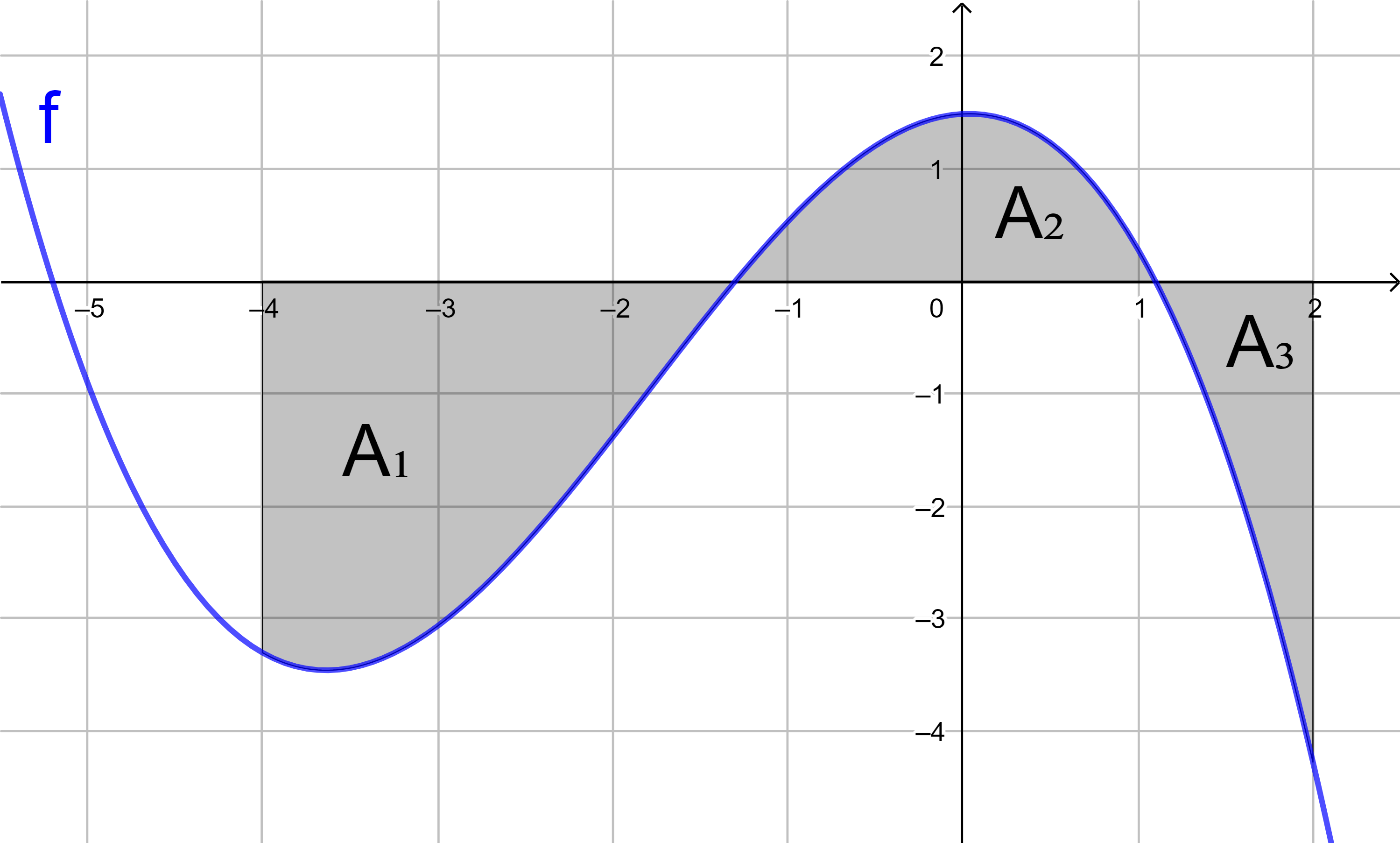
Bestimmen Sie für die Funktion f mit
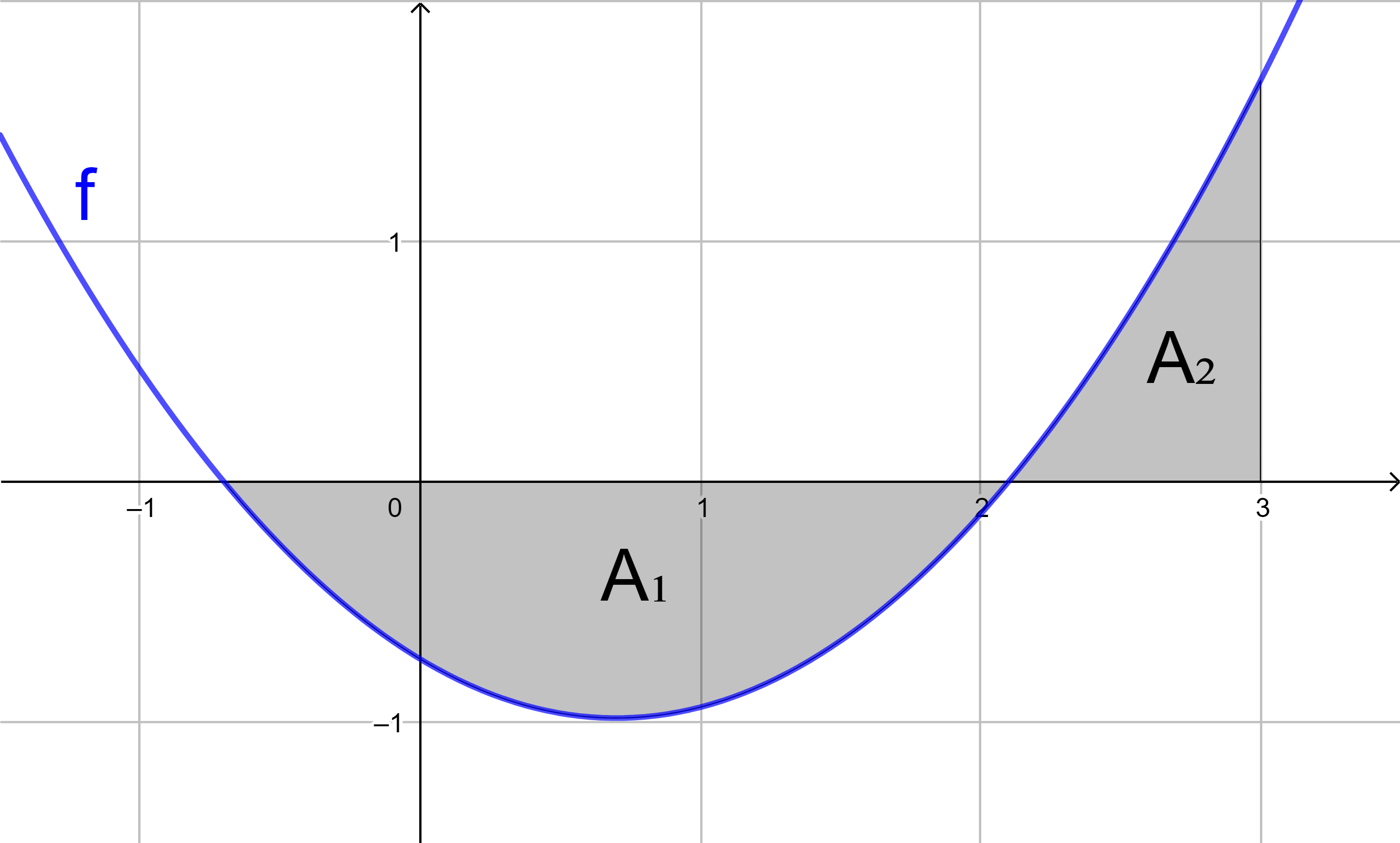
f(x) = -0,5x2 - 0,5x + 1
mit Hilfe von Integralen den Flächeninhalt
der grau markierten Fläche.
Lösung:


Füllen Sie die Eingabefelder aus. Bestimmen Sie die Integralwerte mit dem GTR oder dem Hauptsatz der Differenzial- und Integralrechnung. Runden Sie alle Werte auf die 3. Nachkommastelle.
1. Flächenstück:


 ∫
f(x)
dx =  
A1 =  
  (FE)
2. Flächenstück:


 ∫
f(x)
dx =  
A2 =  
  (FE)
Flächeninhalt insgesamt:    A  =  A1 + A2  =  
  +  
  =  
  (FE)
Kontrolle
Lösung
Nicht immer können die Schnittstellen des Funktionsgraphen mit der x-Achse (die sogenannten "Nullstellen") exakt aus der Zeichnung abgelesen werden. In diesem Fall müssen die Nullstellen von f zunächst rechnerisch ermittelt werden.
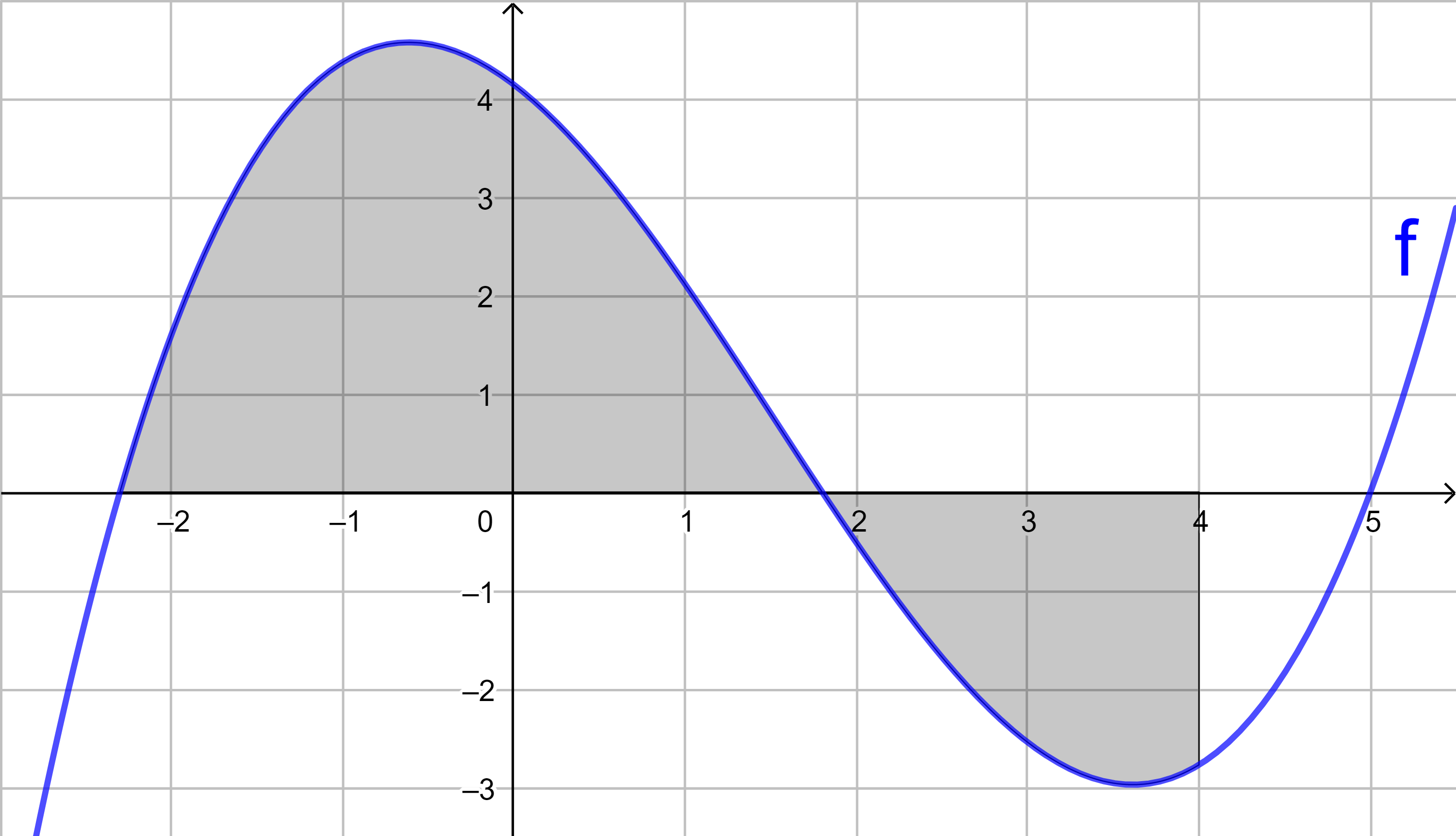
Beispiel 2:
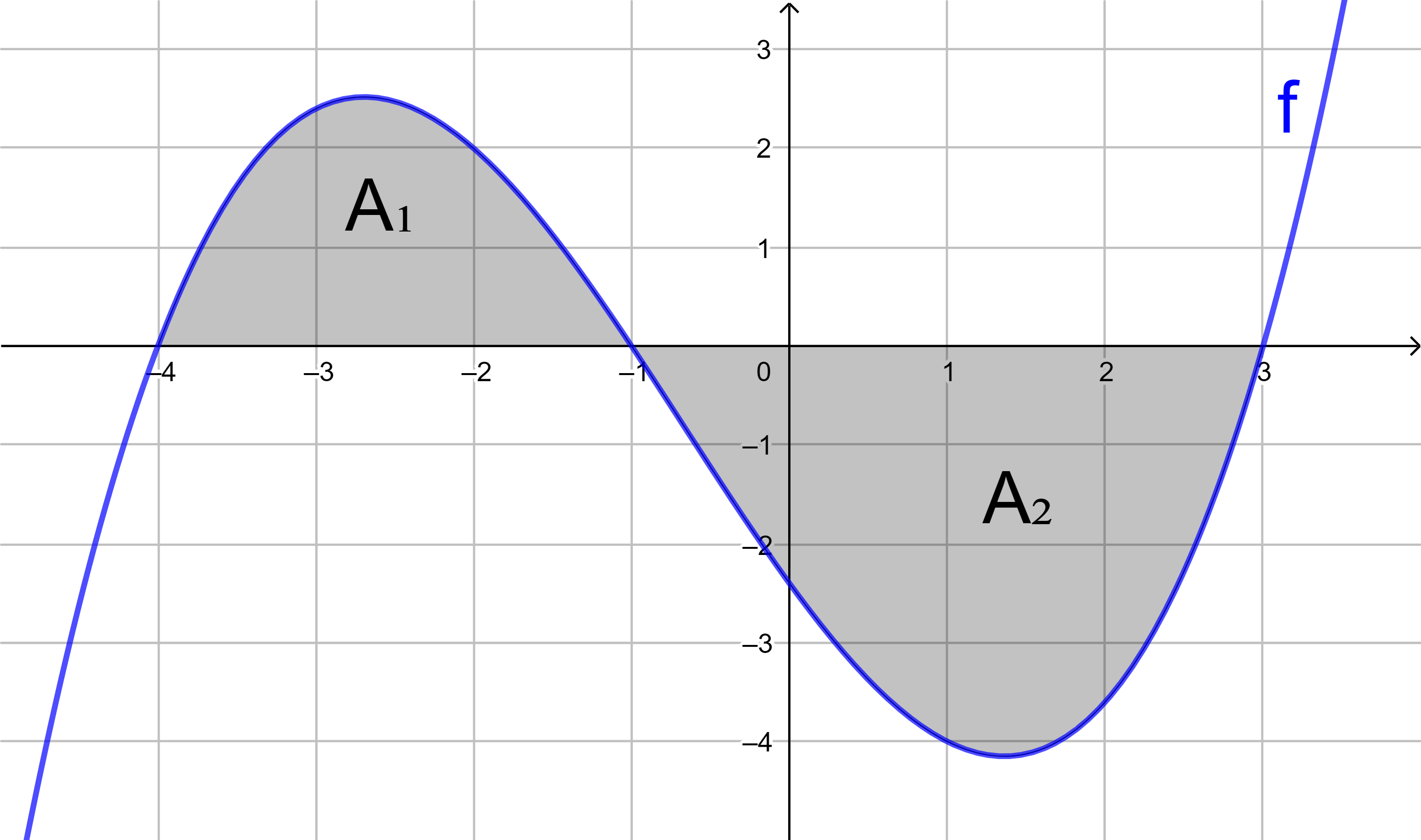
Bestimmen Sie für die Funktion f mit
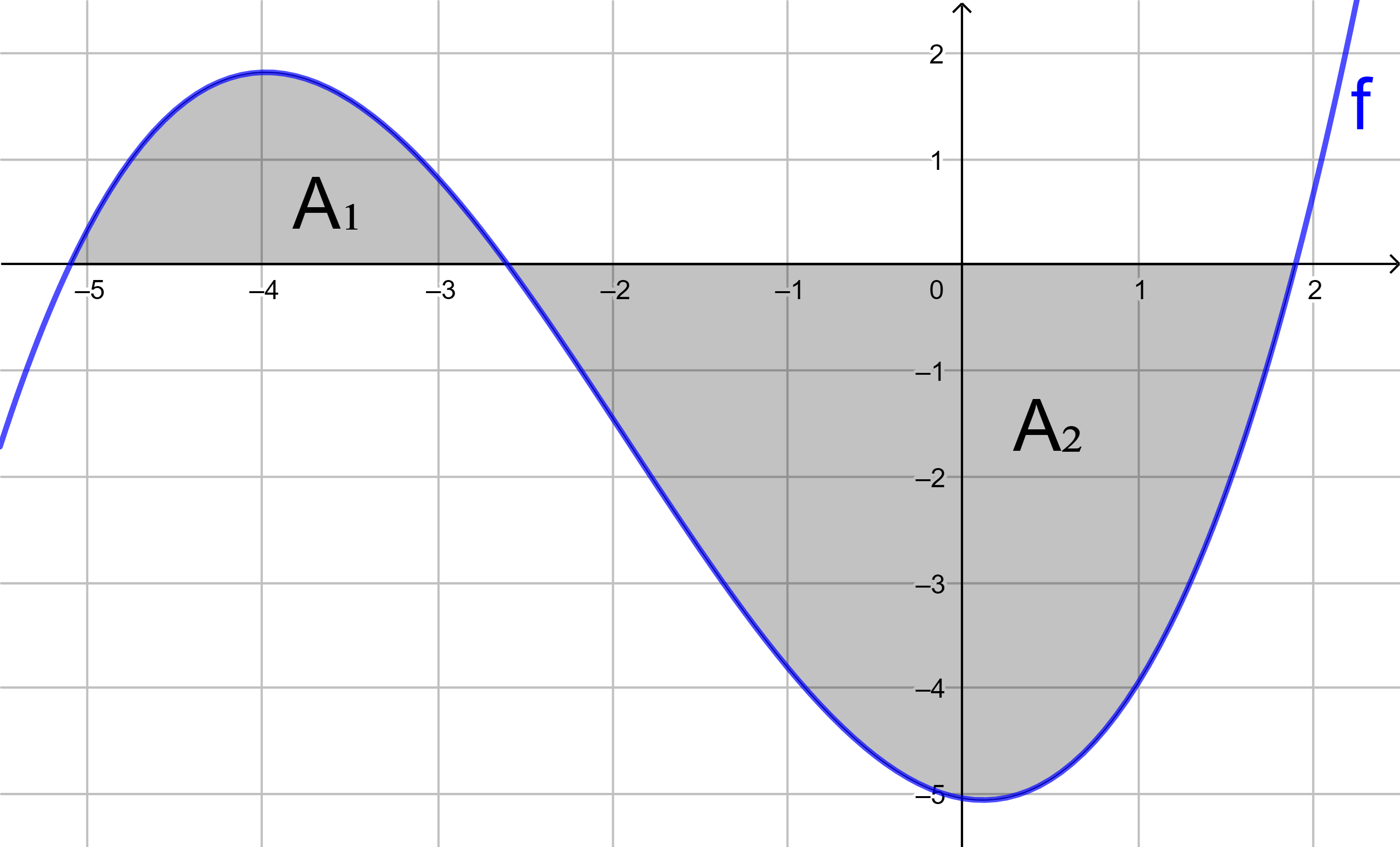
f(x) = 0,2x3 - 0,9x2 - 1,328x + 4,14
mit Hilfe von Integralen den Flächeninhalt
der grau markierten Fläche.
Lösung:
1.  Bestimmung der Nullstellen von f
Ansatz:
f(x) = 0
0,2x3 - 0,9x2 - 1,328x + 4,14 = 0
Lösung der Gleichung mit dem GTR:
x1 = -2,3      x2 = 1,8      x3 = 5
2.  Bestimmung des gesuchten Flächeninhalts
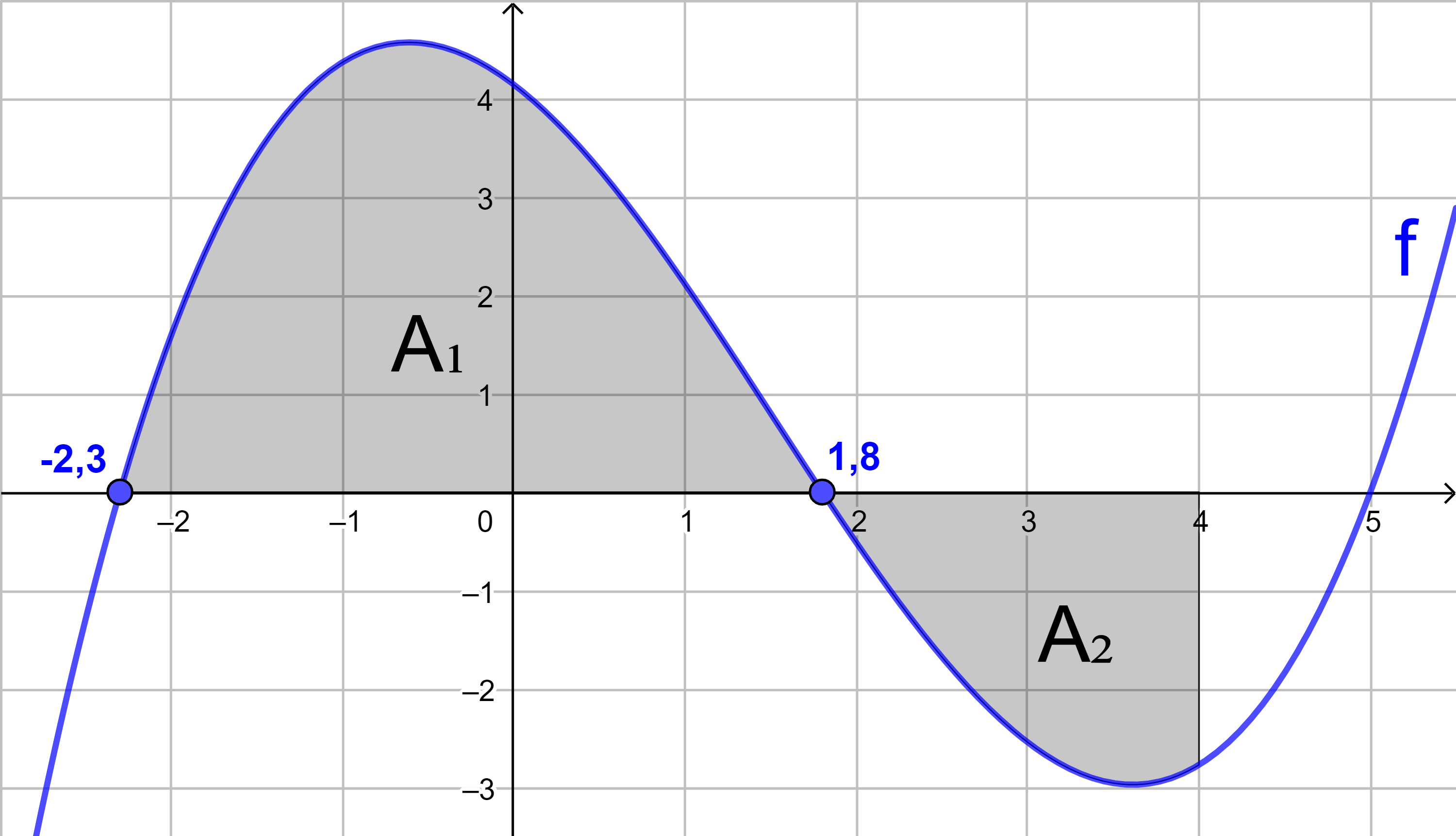
1. Flächenstück:
 1,8
 ∫
f(x)
dx
-2,3
  =  12,061



  A1  =  12,061  (FE)
2. Flächenstück:
 4
 ∫
f(x)
dx
1,8
  =  -4,54



  A2  =  4,54  (FE)
(Die Integralwerte können mit dem GTR oder dem Hauptsatz der Differenzial- und Integralrechnung ermittelt werden.)
Flächeninhalt insgesamt:    A  =  A1  +  A2  =  12,061  +  4,54  =  16,601  (FE)
Sie können die Berechnung von Flächeninhalten nach vorheriger Nullstellenbestimmung jetzt üben. Wählen Sie weitere Aufgaben durch Anklicken aus.
Aufgabe:
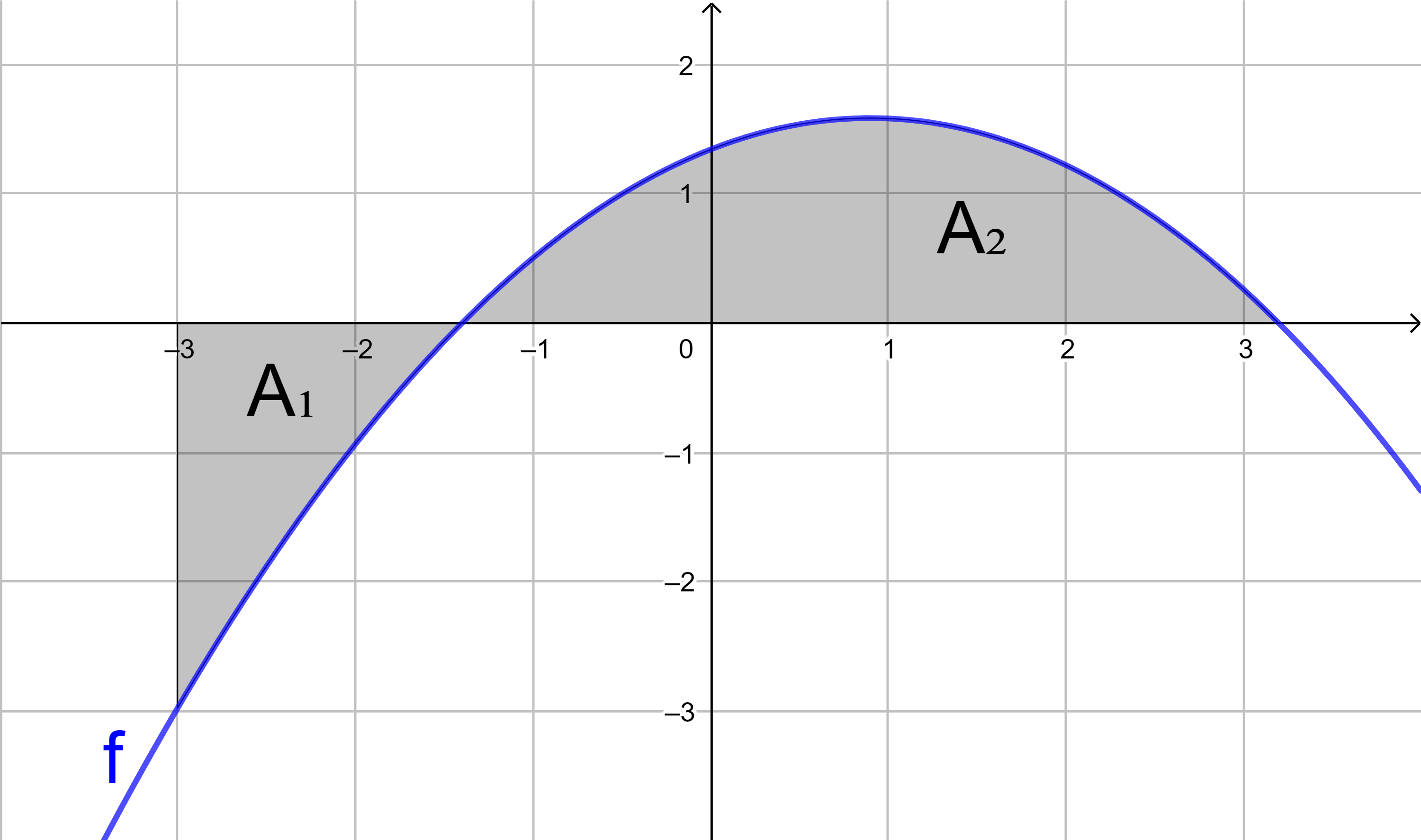
Aufgabe:
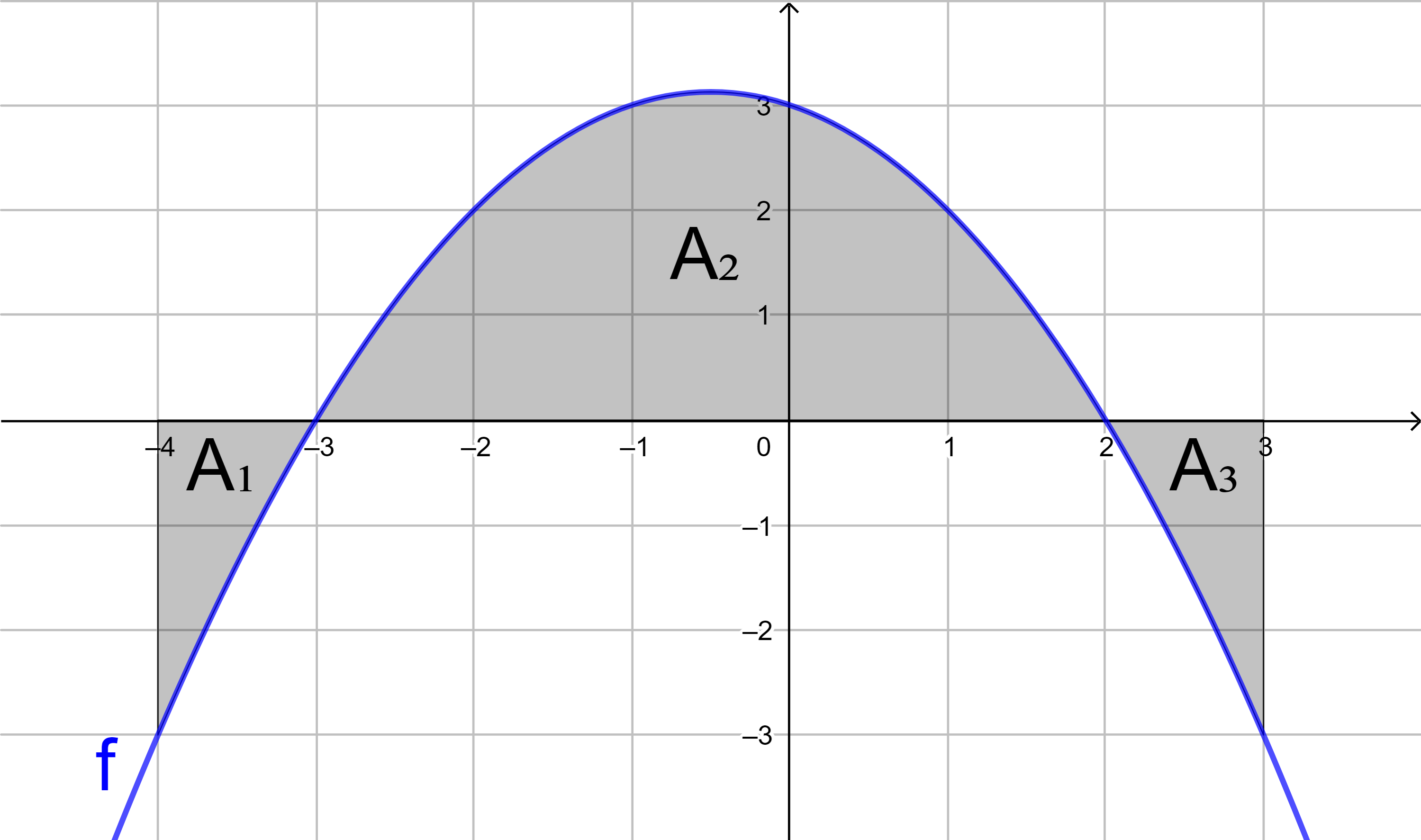
Bestimmen Sie für die Funktion f mit
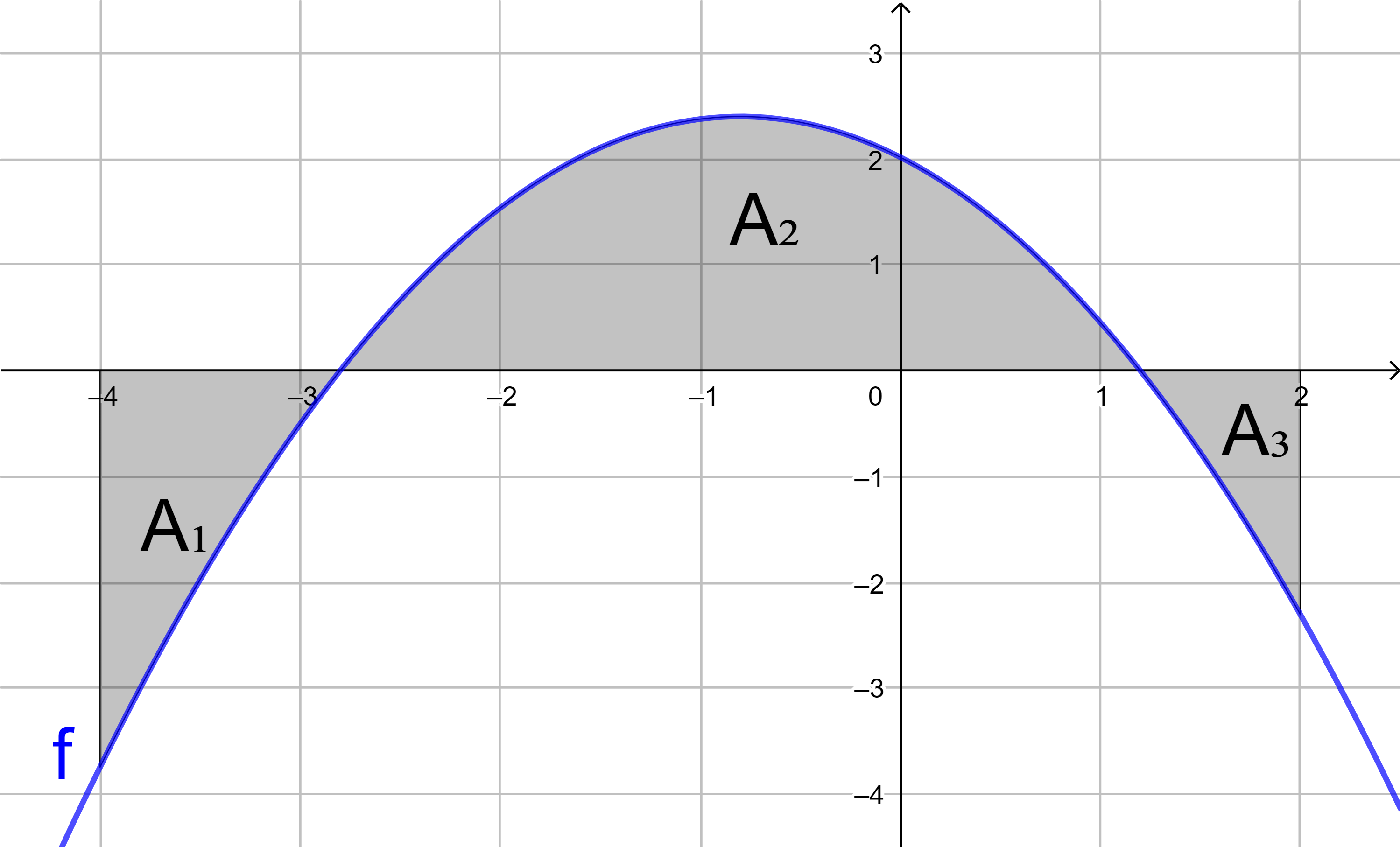
f(x) = -0,3x2 + 0,54x + 1,344
mit Hilfe von Integralen den Flächeninhalt
der grau markierten Fläche.
Lösung:


Füllen Sie die Eingabefelder aus.
1.  Bestimmung der Nullstellen von f
-0,3x2 + 0,54x + 1,344  =  
0,5x2 - 0,7x - 0,735  =  
-0,6x2 - 0,96x + 2,016  =  
0,2x3 + 1,16x2 - 0,274x - 5,0388  =  
-0,8x3 + 6,16x2 - 13,216x + 7,04  =  
-0,2x3 - 1,08x2 + 0,078x + 1,4872  =  
Lösen Sie die Gleichung mit dem GTR oder - falls möglich - mit geeigneten mathematischen Methoden.
x1  =  
x2  =  
(x1 < x2)
x1  =  
x2  =  
x3  =  
(x1 < x2 < x3)
2.  Bestimmung des gesuchten Flächeninhalts
Bestimmen Sie die Integralwerte mit dem GTR oder dem Hauptsatz der Differenzial- und Integralrechnung. Runden Sie alle Werte auf die 3. Nachkommastelle.
1. Flächenstück:


 ∫
f(x)
dx =  
A1 =  
  (FE)
2. Flächenstück:


 ∫
f(x)
dx =  
A2 =  
  (FE)
Flächeninhalt insgesamt:    A  =  A1 + A2  =  
  +  
  =  
  (FE)
Kontrolle
Lösung
Der Hauptsatz der Differenzial- und Integralrechnung ←