Mathe-Training für die Oberstufe - Bestimmung lokaler Extrempunkte (2. Verfahren)
✔
Übung
Aufgabe:
Bestimmen Sie rechnerisch die lokalen Extrempunkte des Graphen von f mit f(x) = 0,4x3 + 1,2x2 + 1,2x + 2.
Erklärung
Verfahren
In allen lokalen Hoch- oder Tiefpunkten einer Funktion f ist die Tangente an den Graphen von f waagerecht, d. h. die Steigung der Tangente ist 0.
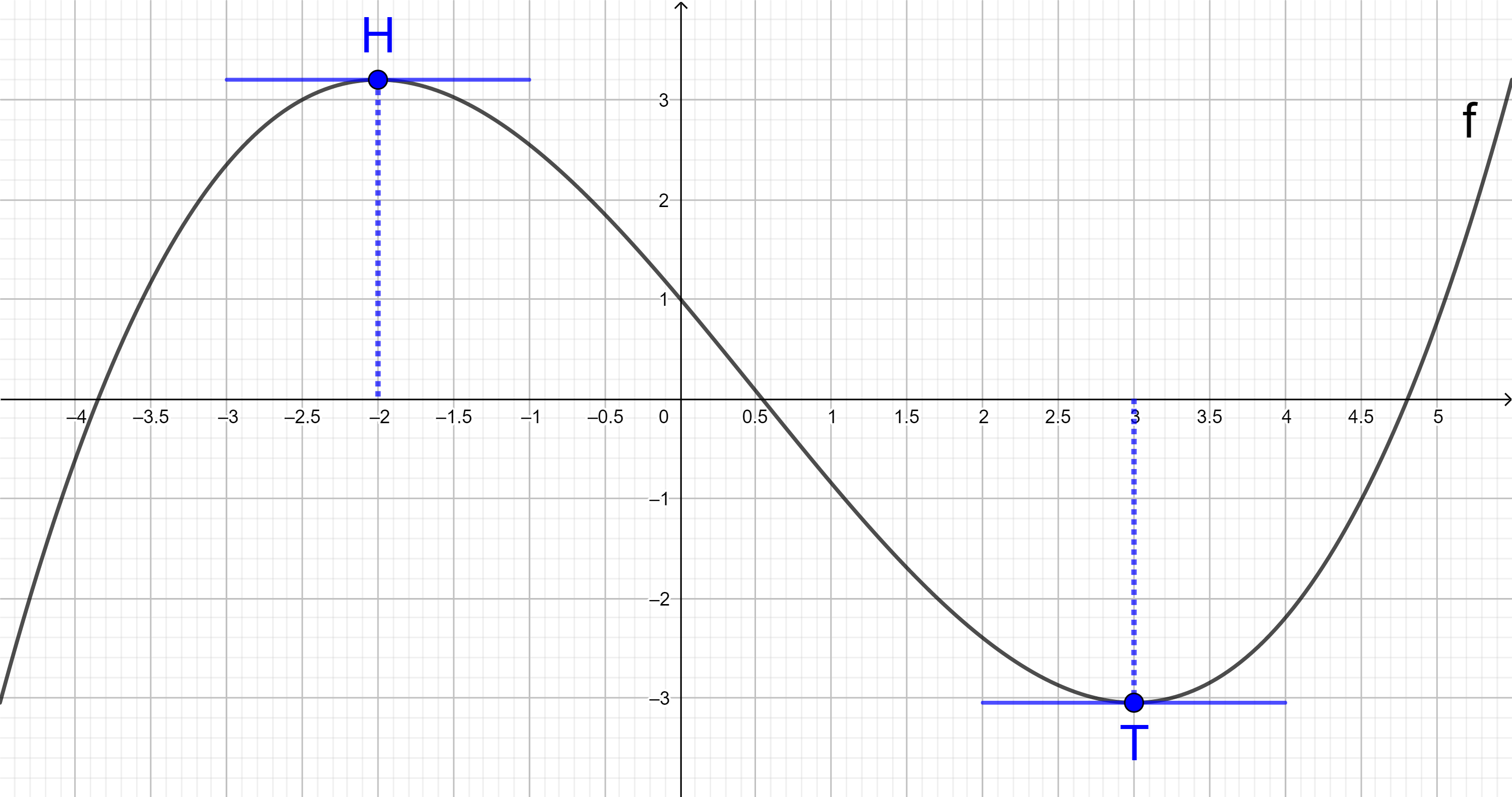
Die Steigung der Tangente wird mit der 1. Ableitung von f berechnet. Die x-Koordinate jedes Extrempunktes (genannt "Extremstelle") muss somit die Gleichung f '(x) = 0 erfüllen.
1. Schritt:
Bestimmung der möglichen Extremstellen
notwendige Bedingung: f '(x) = 0
f '(x) = 1,2x2 + 2,4x + 1,2
(→ Lernprogramm "Ableitung ganzrationaler Funktionen", Kapitel 4.2. Ableitungsregeln)
1,2x2 + 2,4x + 1,2 = 0
Lösung der Gleichung mit dem GTR oder - wenn möglich - mit Hilfe geeigneter mathematischer Methoden (wie z. B. Ausklammern oder p,q-Formel)
Die mögliche Extremstelle lautet:
x = -1
Ein Funktionsgraph hat nicht nur in seinen lokalen Extrempunkten, sondern auch in seinen Sattelpunkten die Steigung 0. Die x-Koordinaten der Sattelpunkte befinden sich somit unter den Lösungen der Gleichung f '(x) = 0 als mögliche Extremstellen.
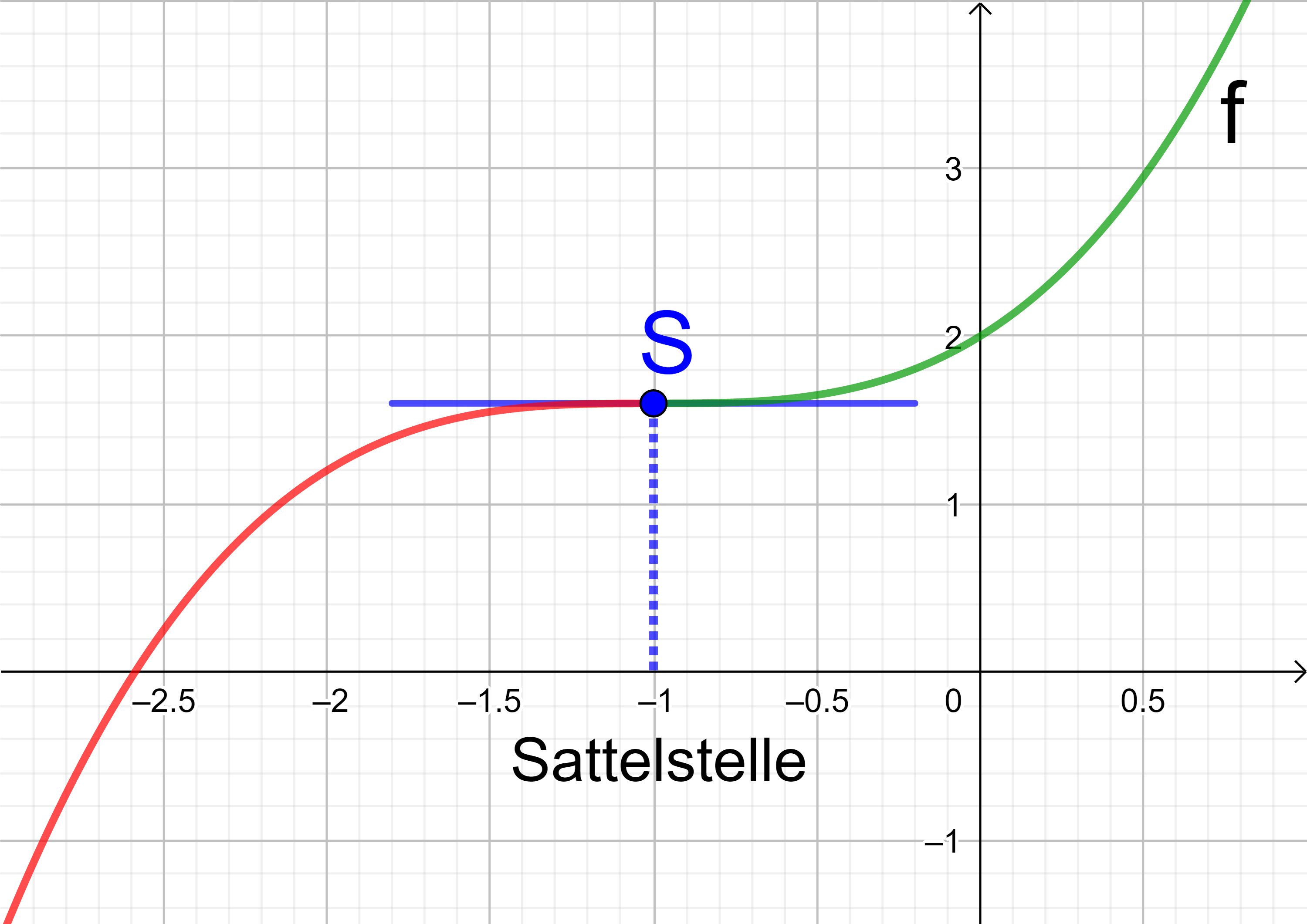
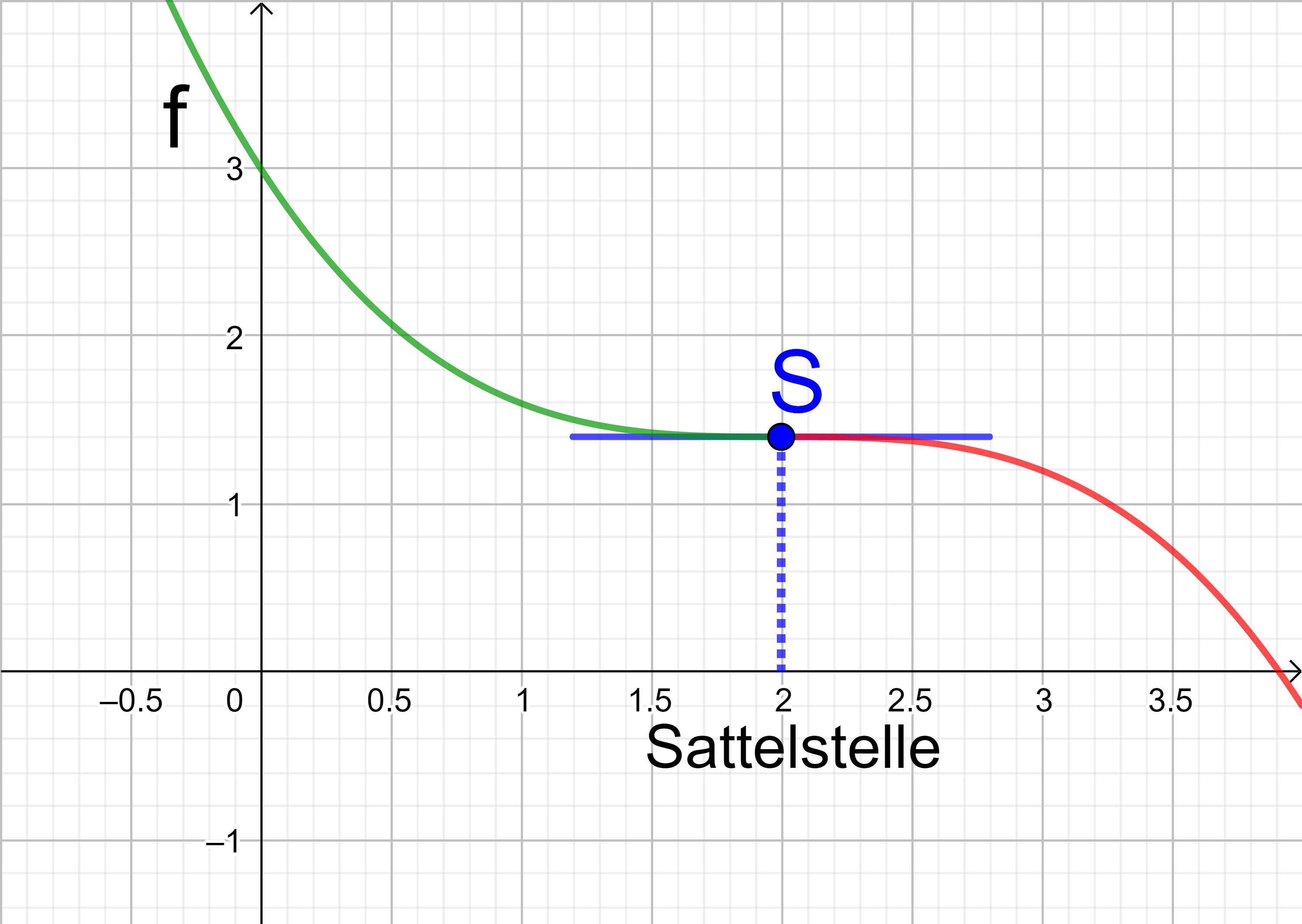
Sattelpunkte sind Wendepunkte, in denen der Funktionsgraph entweder von einer Rechts- in eine Linkskrümmung oder von einer Links- in eine Rechtskrümmung wechselt.
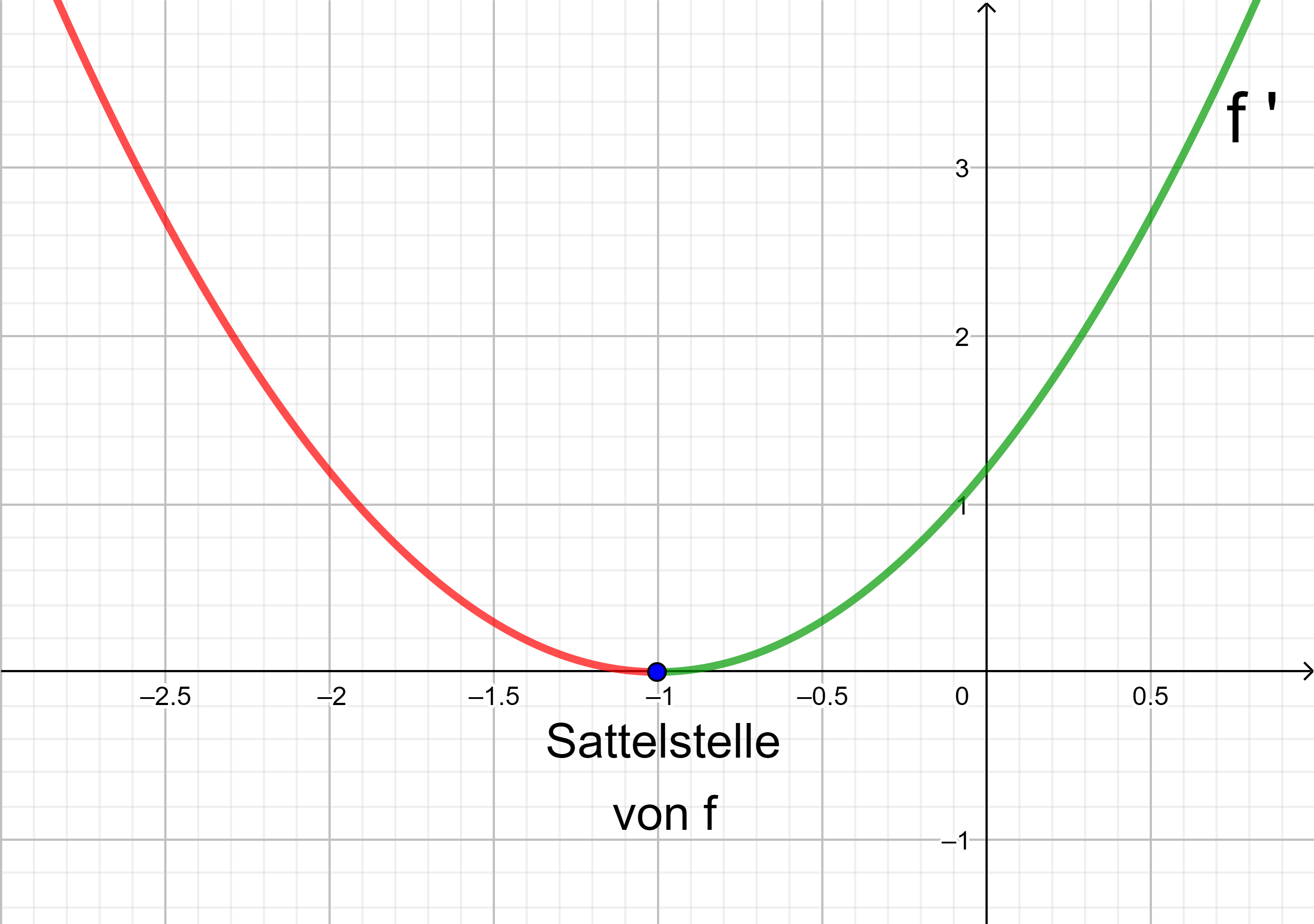
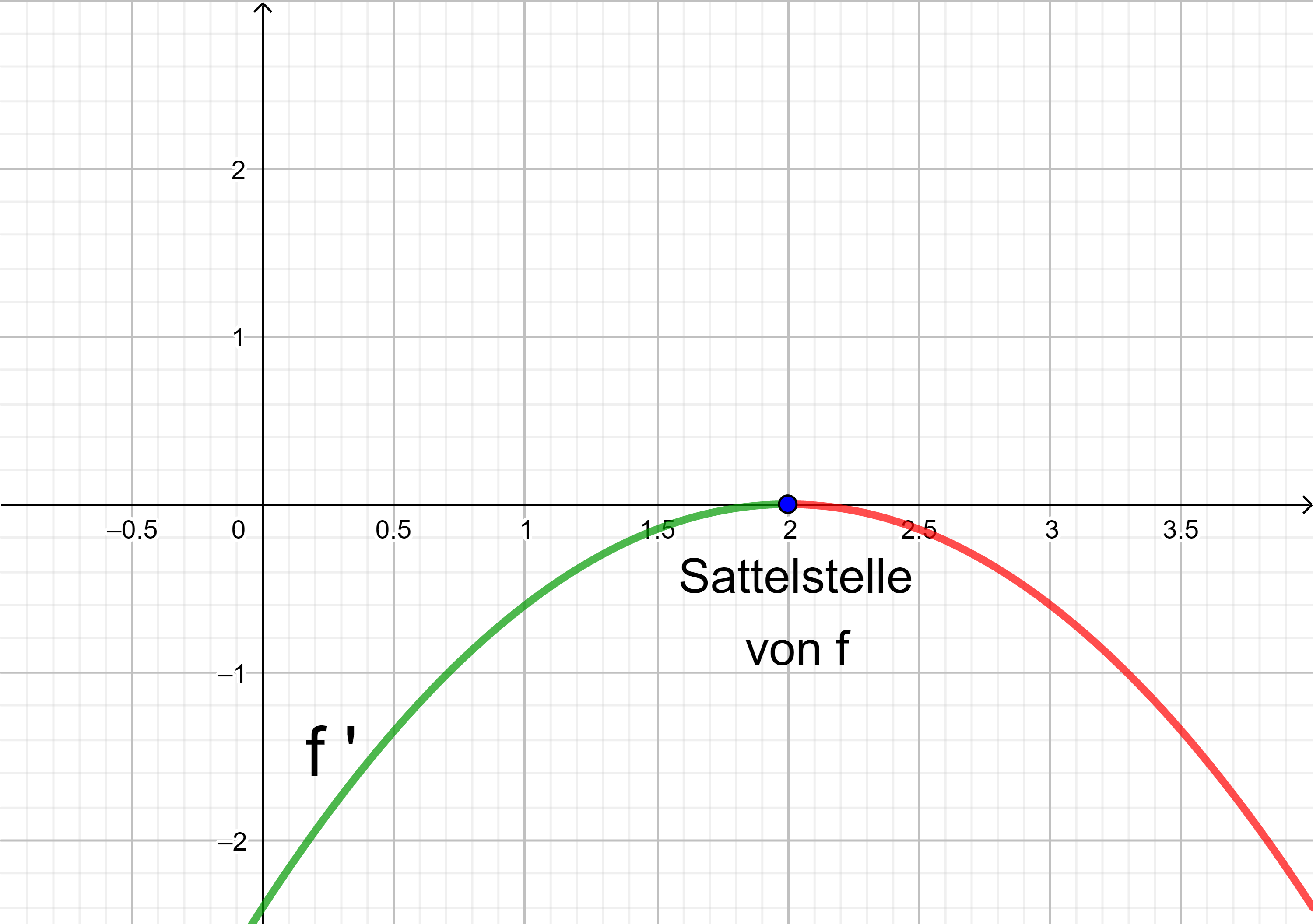
Die Ableitungsfunktion f ' wechselt an der Sattelstelle von f entweder vom Fallen zum Steigen oder vom Steigen zum Fallen. Der Graph von f ' hat an der Sattelstelle von f einen lokalen Extrempunkt.
Deshalb gilt für jede Sattelstelle x0:
f '(x0) = 0 und f ''(x0) = 0
f '(x0) = 0 und f ''(x0) = 0
(Sowohl der Graph von f als auch der Graph von f ' haben an der Stelle x0 die Steigung 0. Die Ableitung von f ' ist f ''.)
Achtung:
Aus f '(x0) = 0 und f ''(x0) = 0 folgt nicht automatisch, dass x0 eine Sattelstelle ist. Es kann sich auch um eine lokale Extremstelle handeln, wie das nachfolgende Beispiel zeigt. Eine weitere Untersuchung (z. B die Anwendung des Vorzeichenwechselkriteriums) ist notwendig.
(→ Lernprogramm "Bestimmung lokaler Extrempunkte (1. Verfahren)", Beispiel 1 und 2)
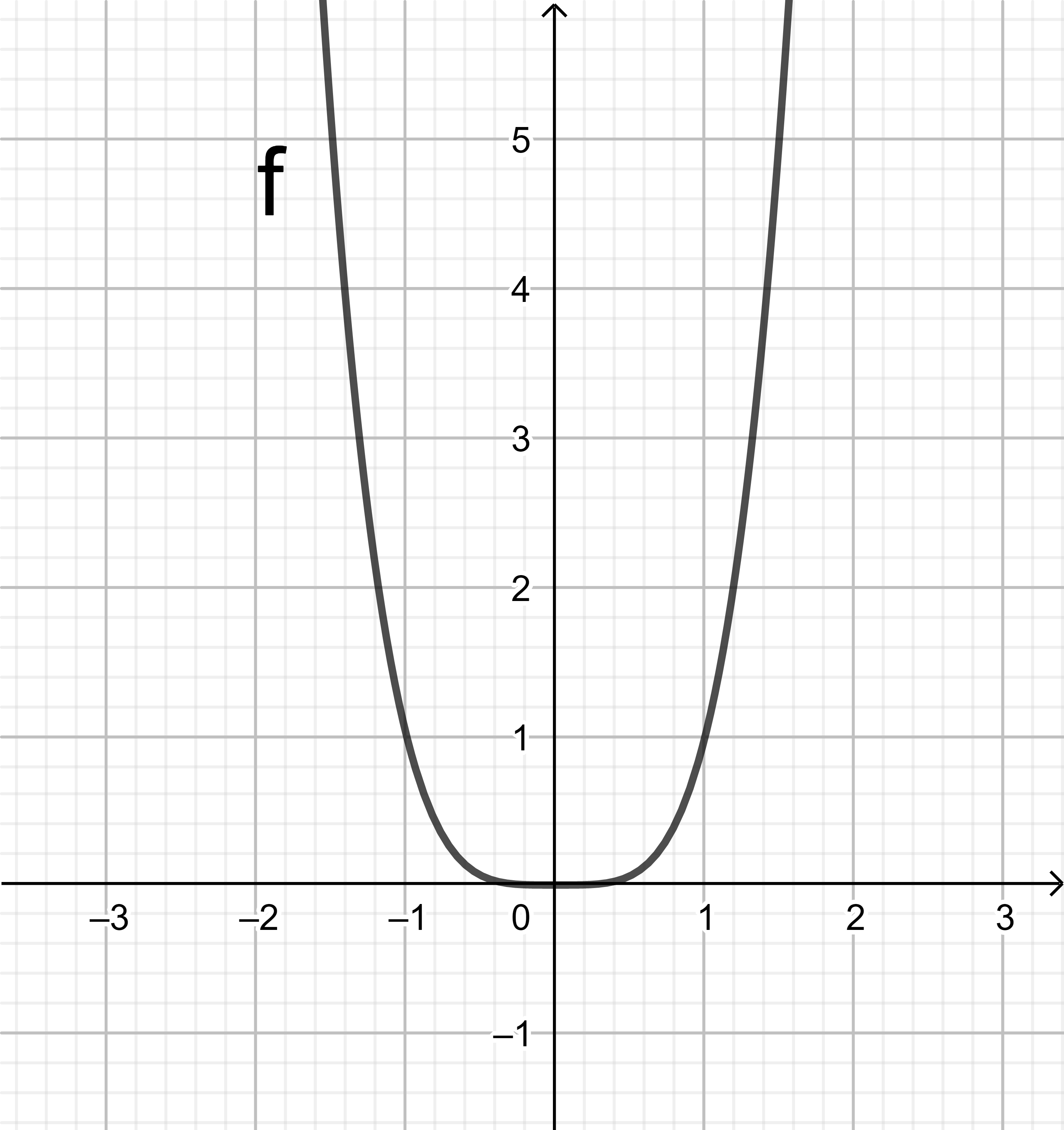
Für die Funktion f mit f(x) = x4 gilt:
f '(x) = 4x3
f ''(x) = 12x2
f '(0) = 0 und f ''(0) = 0
Der Graph von f hat an der Stelle x0 = 0 keinen Sattelpunkt, sondern einen lokalen Tiefpunkt.
2. Schritt:
Untersuchung mit der 2. Ableitung
f ''(x) = 2,4x + 2,4
f ''(-1) = 0
Eine Schlussfolgerung ist nicht möglich. Deshalb wird das Vorzeichen der 1. Ableitung links und rechts von der möglichen Extremstelle untersucht.

↓
↓
f '(-2) = 1,2 > 0
f '(0) = 1,2 > 0
Auswertung mit dem Vorzeichenwechselkriterium:
f ' hat an der Stelle x = -1 keinen Vorzeichenwechsel.
Der Graph von f hat deshalb an der Stelle
x = -1 einen Sattelpunkt. Er hat keine lokalen Extrempunkte.
Der Graph von f hat deshalb an der Stelle
x = -1 einen Sattelpunkt. Er hat keine lokalen Extrempunkte.
3. Schritt:
Angabe des Sattelpunktes
f(-1) = 1,6
Sattelpunkt: S(-1 | 1,6)