Mathe-Training für die Oberstufe - Bestimmung von Wendepunkten
✔
Beispiel 1
Übung
Aufgabe:
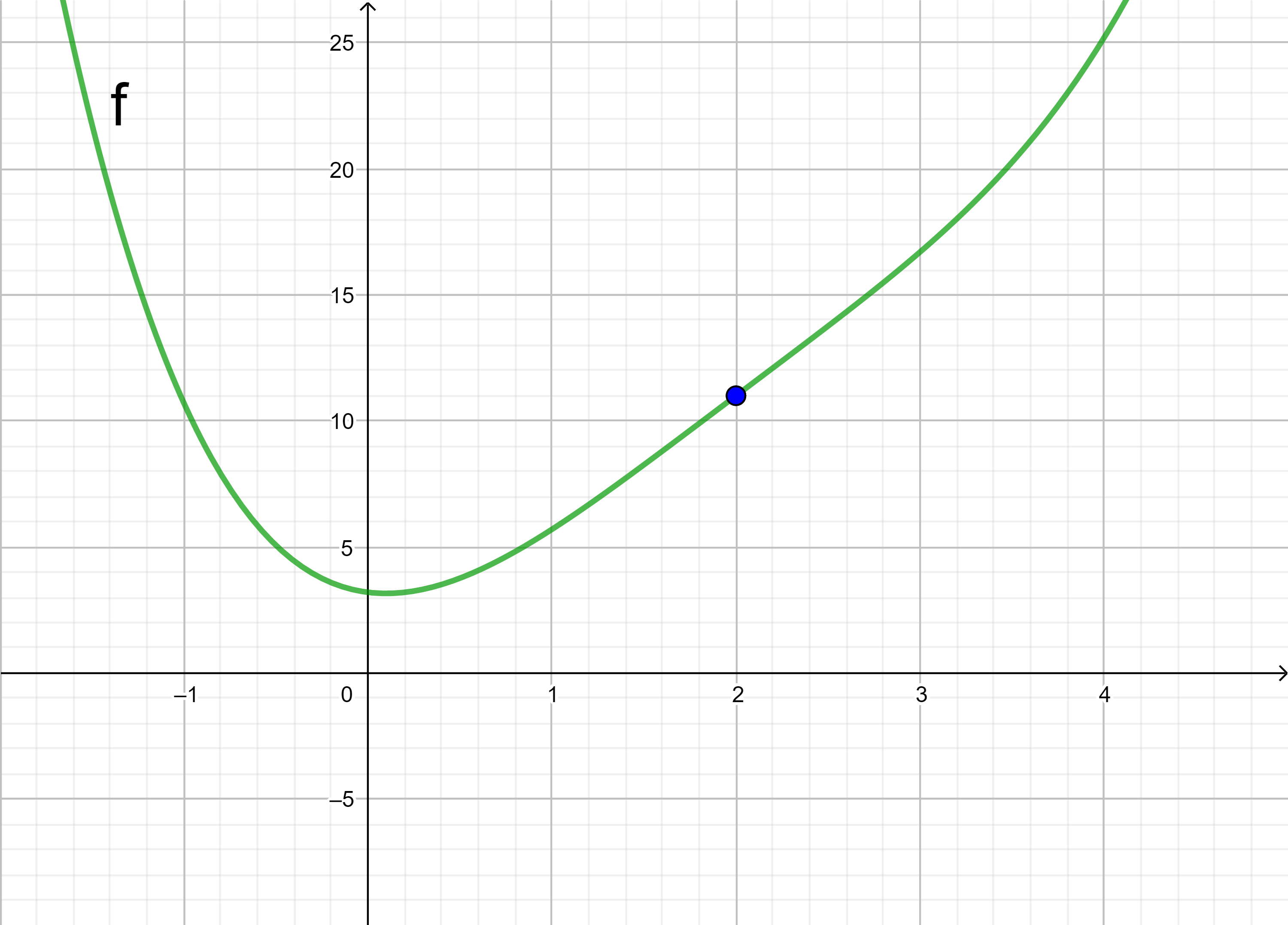
Bestimmen Sie rechnerisch die Wendepunkte des Graphen von f mit f(x) = 0,2x4 - 1,6x3 + 4,8x2 - 0,9x + 3,2.
Erklärung
Verfahren
1. Schritt:
Bestimmung der möglichen Wendestellen
notwendige Bedingung: f ''(x) = 0
f '(x) = 0,8x3 - 4,8x2 + 9,6x - 0,9
f ''(x) = 2,4x2 - 9,6x + 9,6
(→ Lernprogramm "Ableitung ganzrationaler Funktionen", Kapitel 4.2. Ableitungsregeln)
2,4x2 - 9,6x + 9,6 = 0
Lösung der Gleichung mit dem GTR oder mit Hilfe geeigneter mathematischer Methoden (wie z. B. Umformen der Gleichung nach x, Ausklammern von x oder p,q-Formel)
Die mögliche Wendestelle lautet:
x = 2
Ein Wendepunkt ist ein Punkt, in dem der Funktionsgraph entweder von einer Rechts- in eine Linkskrümmung oder von einer Links- in eine Rechtskrümmung wechselt.
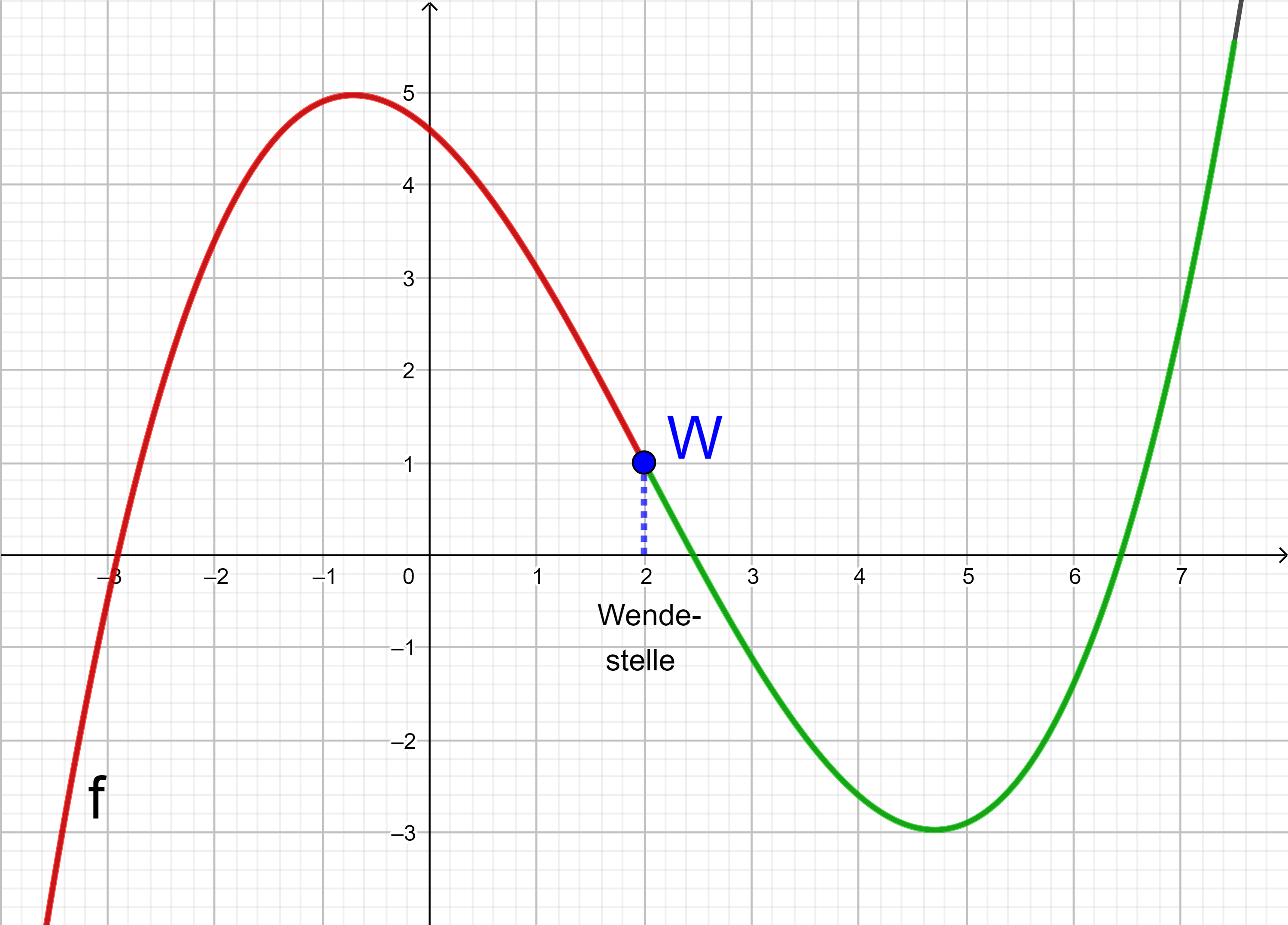

Auf einem rechtsgekrümmten Abschnitt des Funktionsgraphen nimmt die Steigung des Graphen kontinuierlich ab, auf einem linksgekrümmten Abschnitt kontinuierlich zu.
Klicken Sie
hier,
um die Änderung der Steigung im Verlauf des Funktionsgraphen mit Hilfe einer Animation zu veranschaulichen.
Der Graph der Ableitungsfunktion f ' (mit der die Steigung des Graphen von f berechnet wird) fällt deshalb in dem Intervall, in dem der Graph von f rechtsgekrümmt ist, und steigt in dem Intervall, in dem der Graph von f linksgekrümmt ist.
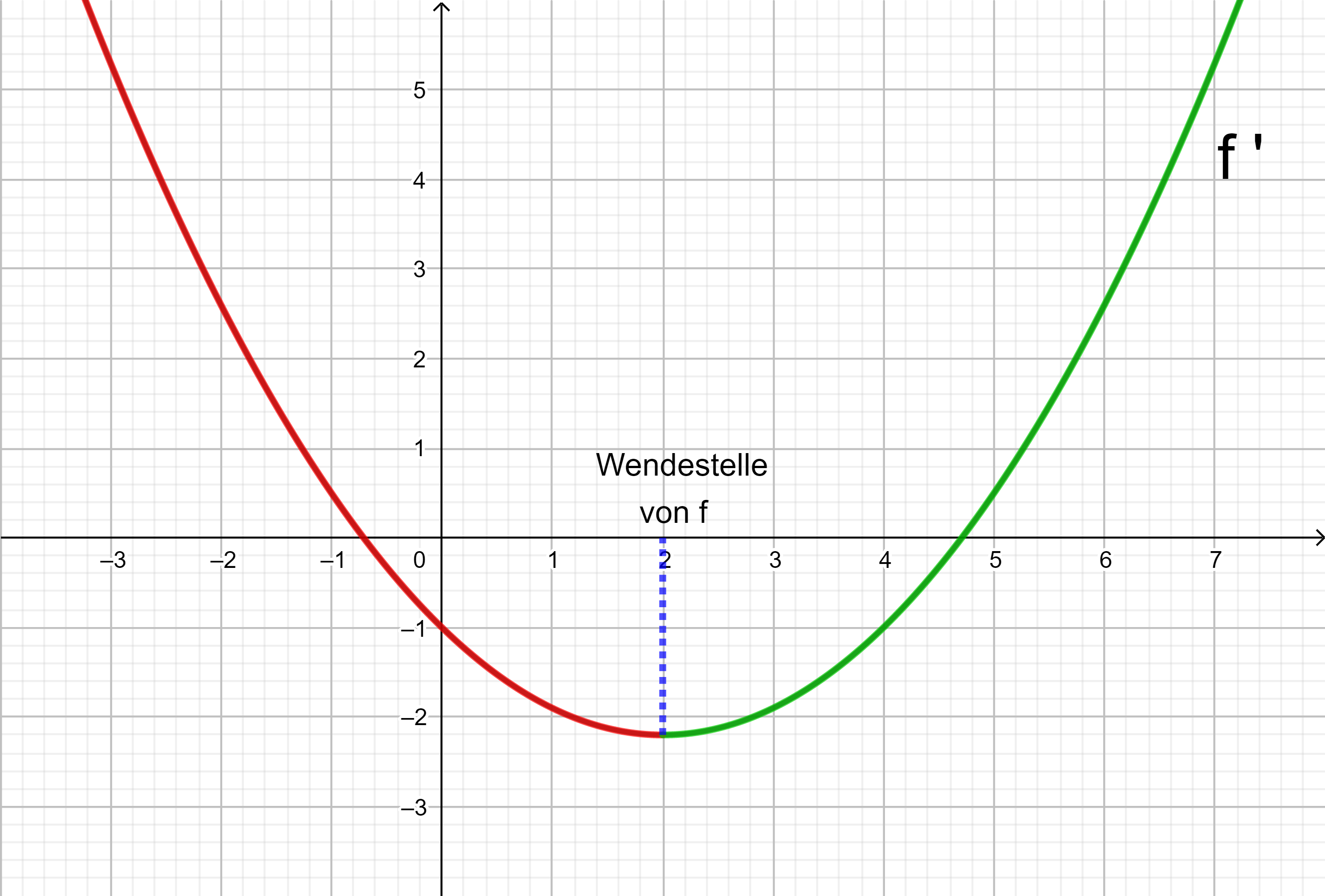
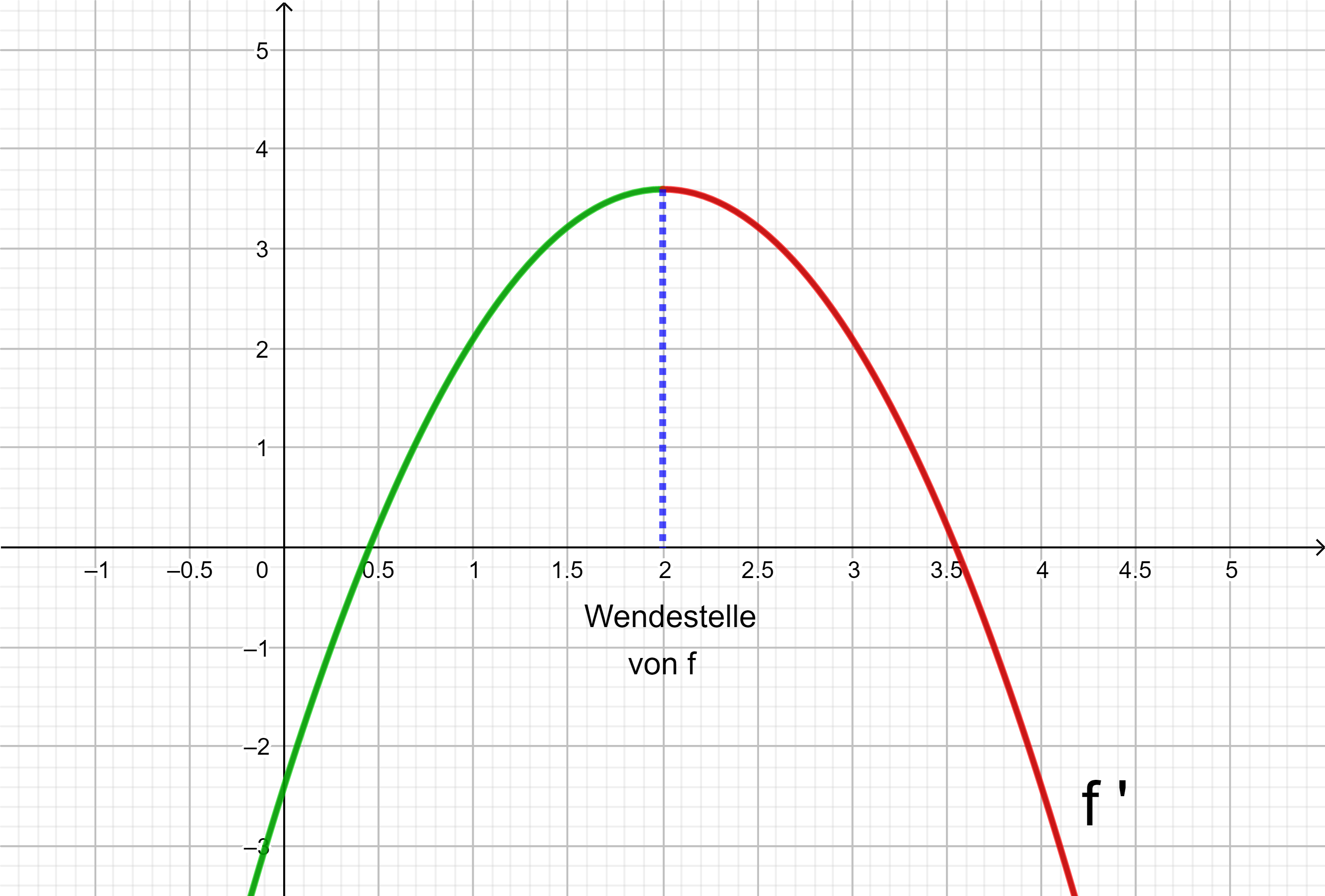
Mit der Ableitungsfunktion f '' wird die Steigung des Graphen von f ' berechnet.
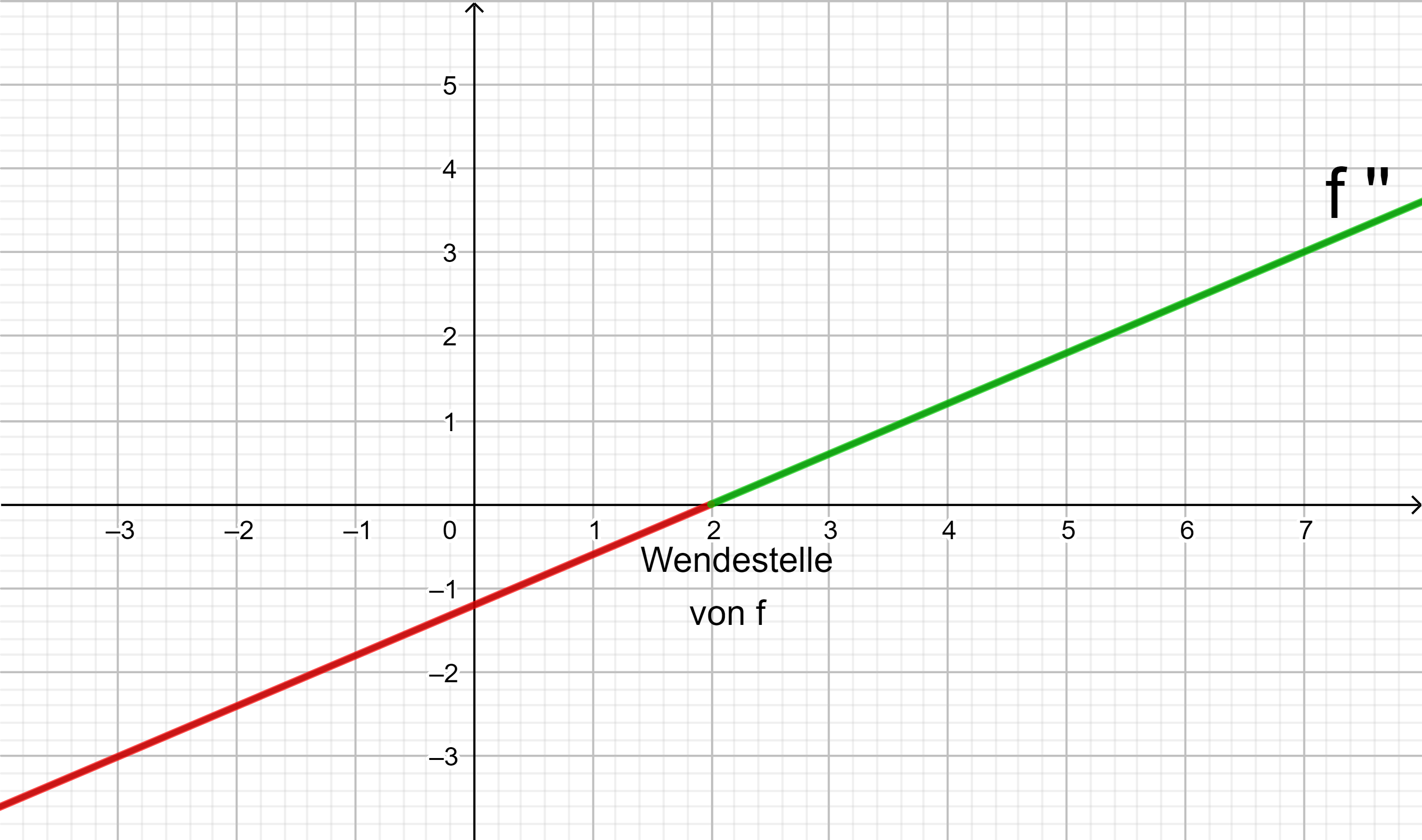
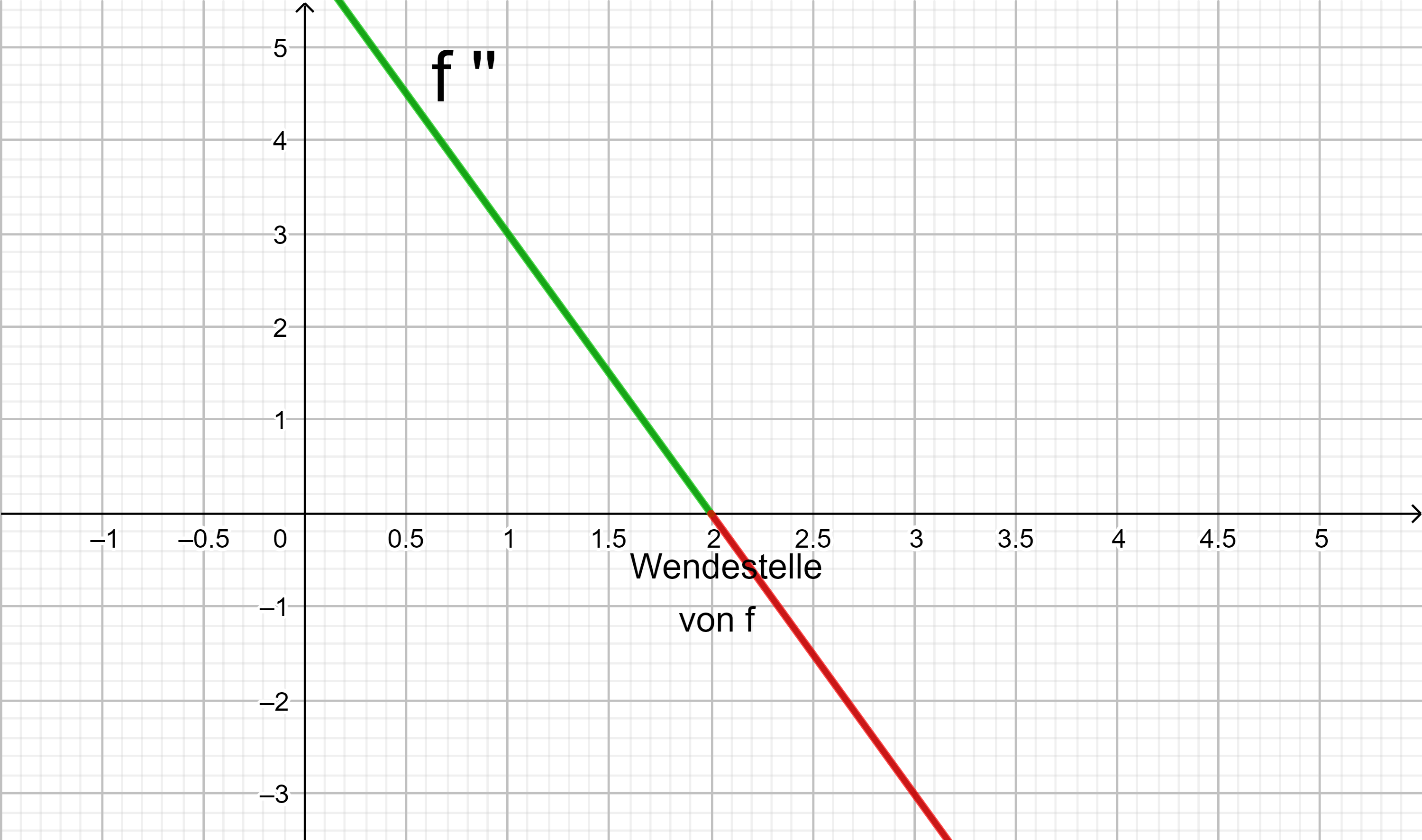
Ist f ''(x) < 0 in einem Intervall, fällt der Graph von f’ in diesem Intervall und der Graph von f ist rechtsgekrümmt.
Ist f ''(x) > 0 in einem Intervall, steigt der Graph von f’ in diesem Intervall und der Graph von f ist linksgekrümmt.
Wechselt f '' an einer Stelle x0 das Vorzeichen, ist x0 eine Wendestelle von f.
Hinweis: Dieses Kriterium kann man anwenden, wenn für eine mögliche Wendestelle x0 gilt: f’’(x0) = 0 und f’’’(x0) = 0. Dann ist nämlich keine Schlussfolgerung auf einen Krümmungswechsel an der Stelle x0 möglich.
Ist f ''(x) > 0 in einem Intervall, steigt der Graph von f’ in diesem Intervall und der Graph von f ist linksgekrümmt.
Wechselt f '' an einer Stelle x0 das Vorzeichen, ist x0 eine Wendestelle von f.
Hinweis: Dieses Kriterium kann man anwenden, wenn für eine mögliche Wendestelle x0 gilt: f’’(x0) = 0 und f’’’(x0) = 0. Dann ist nämlich keine Schlussfolgerung auf einen Krümmungswechsel an der Stelle x0 möglich.
2. Schritt:
Untersuchung mit der 3. Ableitung
f '''(x) = 4,8x - 9,6
f '''(2) = 0
Eine Schlussfolgerung ist nicht möglich. Deshalb wird das Vorzeichen der 2. Ableitung links und rechts von der möglichen Wendestelle untersucht.
Die mögliche Wendestelle unterteilt die x-Achse in zwei Krümmungsintervalle, in denen der Graph von f entweder nur rechtsgekrümmt oder nur linksgekrümmt ist. Aus jedem Krümmungsintervall wird eine beliebige Zahl ausgewählt und in f’’(x) eingesetzt, um das Vorzeichen von f’’ im jeweiligen Intervall zu ermitteln.
Die mögliche Wendestelle unterteilt die x-Achse in zwei Krümmungsintervalle, in denen der Graph von f entweder nur rechtsgekrümmt oder nur linksgekrümmt ist. Aus jedem Krümmungsintervall wird eine beliebige Zahl ausgewählt und in f’’(x) eingesetzt, um das Vorzeichen von f’’ im jeweiligen Intervall zu ermitteln.

↓
↓
f ''(0) = 2,4 > 0
f ''(3) = 9,6 > 0
Der Graph von f ist sowohl im Intervall
]−∞ ; 2[
als auch im Intervall
]2 ; + ∞[
linksgekrümmt.
2 ist keine Wendestelle. Der Graph von f hat keinen Wendepunkt.