5. Baumdiagramm und Pfadregeln

← Kapitelübersicht
Bernoulli-Ketten sind mehrstufige Zufallsversuche. Sie können mit Hilfe von Baumdiagrammen dargestellt werden. Die verschiedenen Pfade geben die möglichen Abläufe des Zufallsexperiments an und stellen jeweils ein Ergebnis des Zufallsversuchs dar. Auf jeder Stufe stehen an den Ästen die Wahrscheinlichkeiten für Treffer bzw. Niete des Bernoulli-Experiments.
Angenommen, das Glücksrad aus Kapitel 1 soll nicht 5-mal, sondern nur 2-mal hintereinander gedreht werden. Das Glücksspiel wäre dann eine Bernoulli-Kette der Länge 2, die mit dem nachfolgenden Baumdiagramm dargestellt werden könnte:
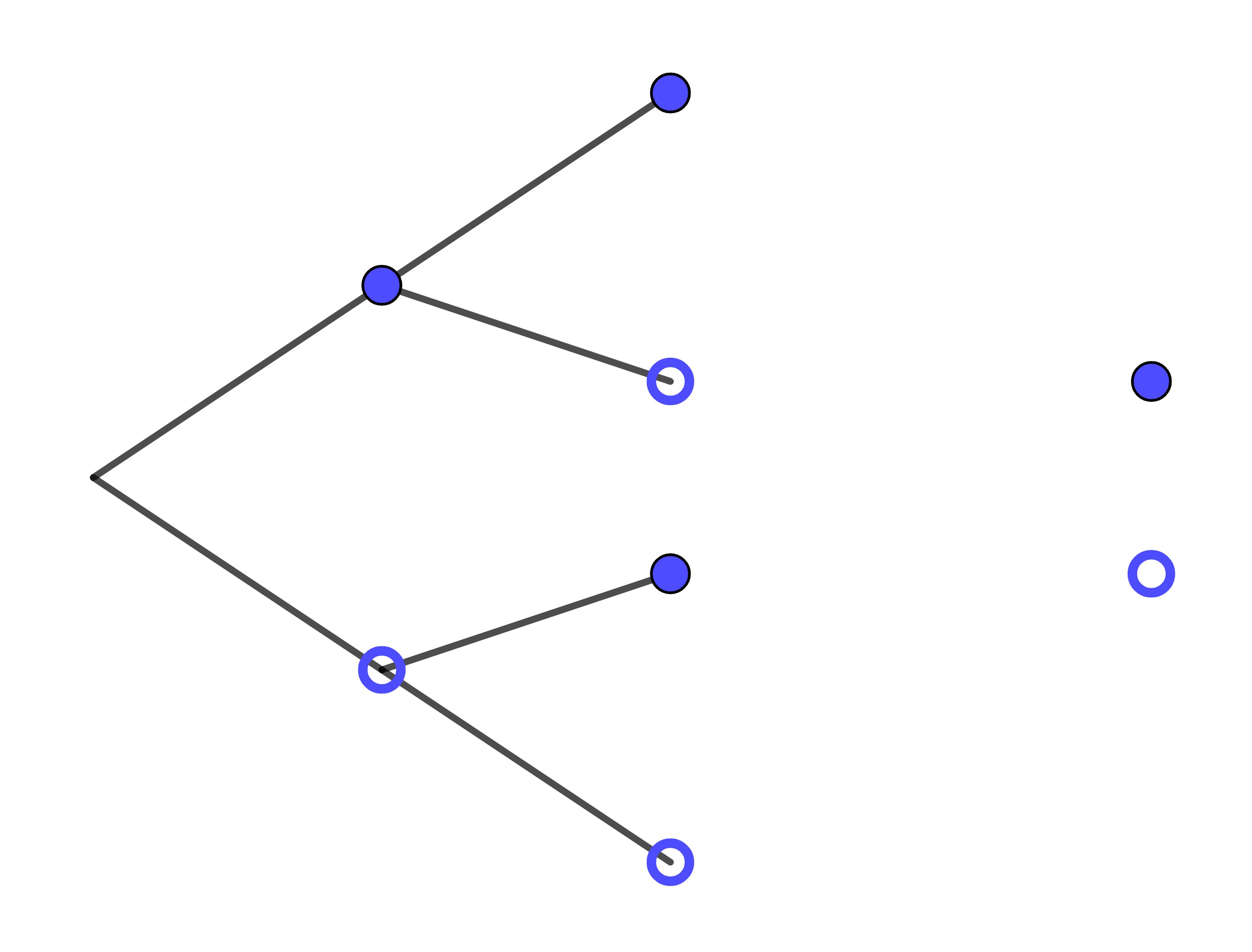
1. Stufe
(1. Drehung)
2. Stufe
(2. Drehung)
1
4
3
4
1
4
3
4
1
4
3
4
=  Treffer (Zeiger auf blauem Feld)
=  Niete (Zeiger nicht auf blauem Feld)
Der zweistufige Zufallsversuch hat vier mögliche Ergebnisse, deren Wahrscheinlichkeit mit Hilfe der ersten Pfadregel berechnet werden kann. Diese lautet:
Die Wahrscheinlichkeit eines Ergebnisses bei einem mehrstufigen Zufallsversuch wird berechnet, indem man alle Wahrscheinlichkeiten entlang des Pfades, der zu diesem Ergebnis gehört, multipliziert.
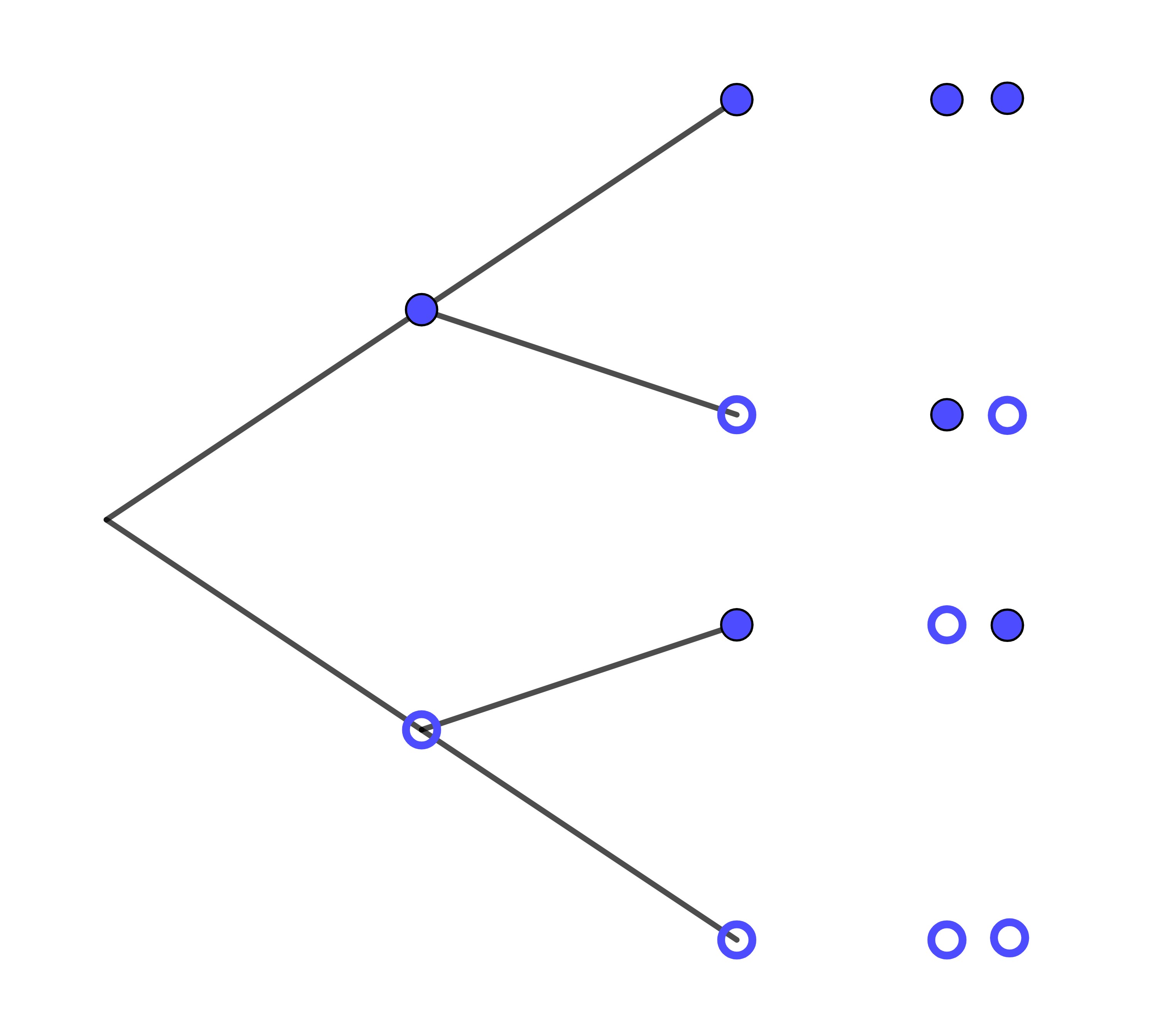
1. Stufe
(1. Drehung)
2. Stufe
(2. Drehung)
Ergebnis
Wahrscheinlichkeit
1
4
3
4
1
4
3
4
1
4
3
4
1
4
  ·  
1
4
  =  
1
16
1
4
  ·  
3
4
  =  
3
16
3
4
  ·  
1
4
  =  
3
16
3
4
  ·  
3
4
  =  
9
16
Bei Bernoulli-Ketten interessiert man sich für die Frage, wie viele Treffer eingetreten sind. Zum Ereignis E "es gibt mindestens einen Treffer" gehören die ersten drei Ergebnisse des oben abgebildeten Baumdiagramms. Die Wahrscheinlichkeit des Ereignisses wird berechnet, indem man die Wahrscheinlichkeiten der zugehörigen Ergebnisse addiert (2. Pfadregel).
1. Stufe
(1. Drehung)
2. Stufe
(2. Drehung)
Ergebnis
Wahrscheinlichkeit
1
4
3
4
1
4
3
4
1
4
3
4
1
4
  ·  
1
4
  =  
1
16
1
4
  ·  
3
4
  =  
3
16
3
4
  ·  
1
4
  =  
3
16
P(E)  =  
1
16
  +  
3
16
  +  
3
16
  =  
7
16
Übung:
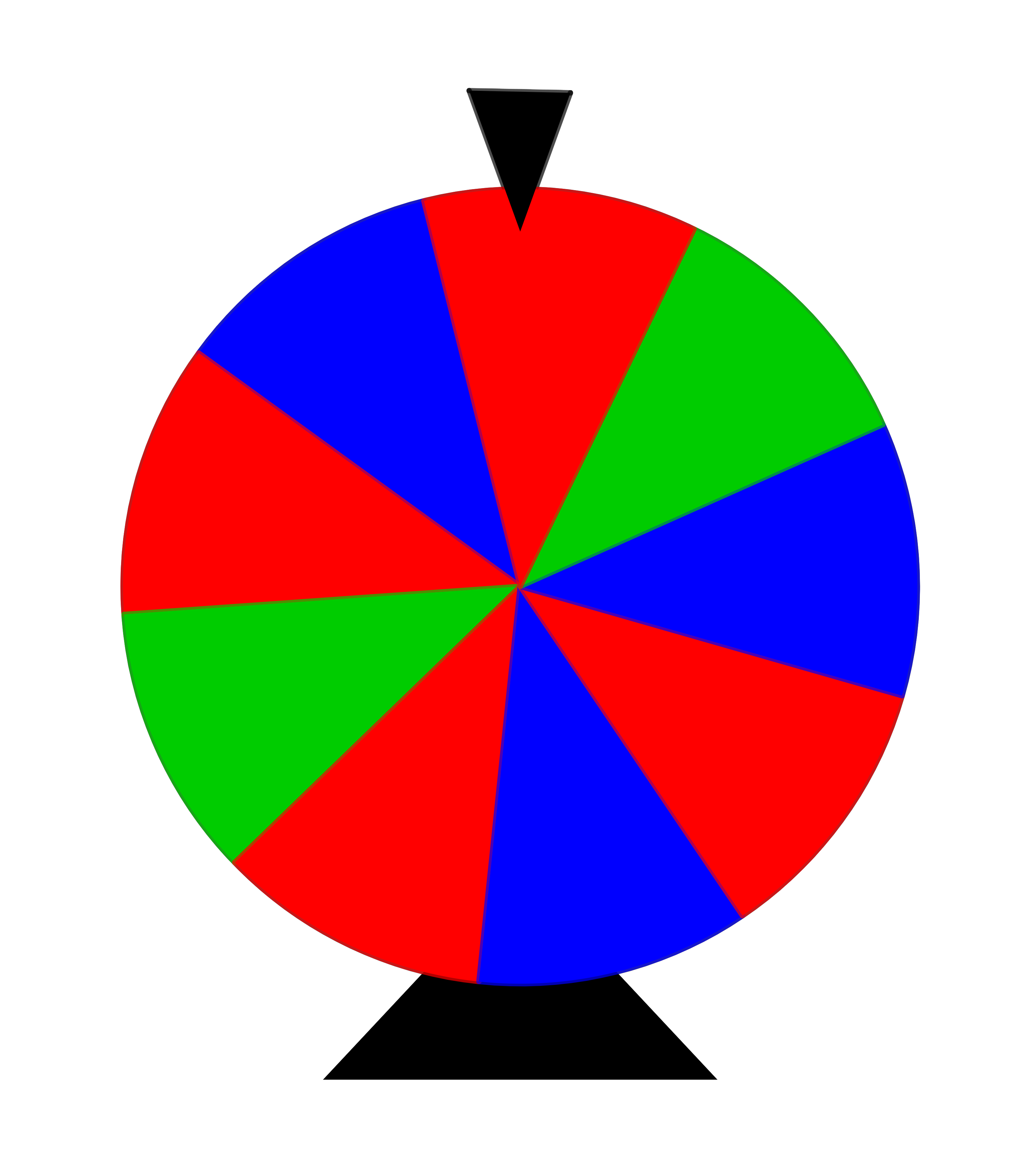
Das links abgebildete Glücksrad soll zweimal hintereinander gedreht werden.
Als Treffer gilt: Nach der Drehung steht der Zeiger auf einem roten Feld.


Tragen Sie in dem nachfolgenden zugehörigen Baumdiagramm die Wahrscheinlichkeiten entlang der Pfade und für die einzelnen Ergebnisse ein. Berechnen Sie die Wahrscheinlichkeit des Ereignisses E: Es gibt höchstens einen Treffer.
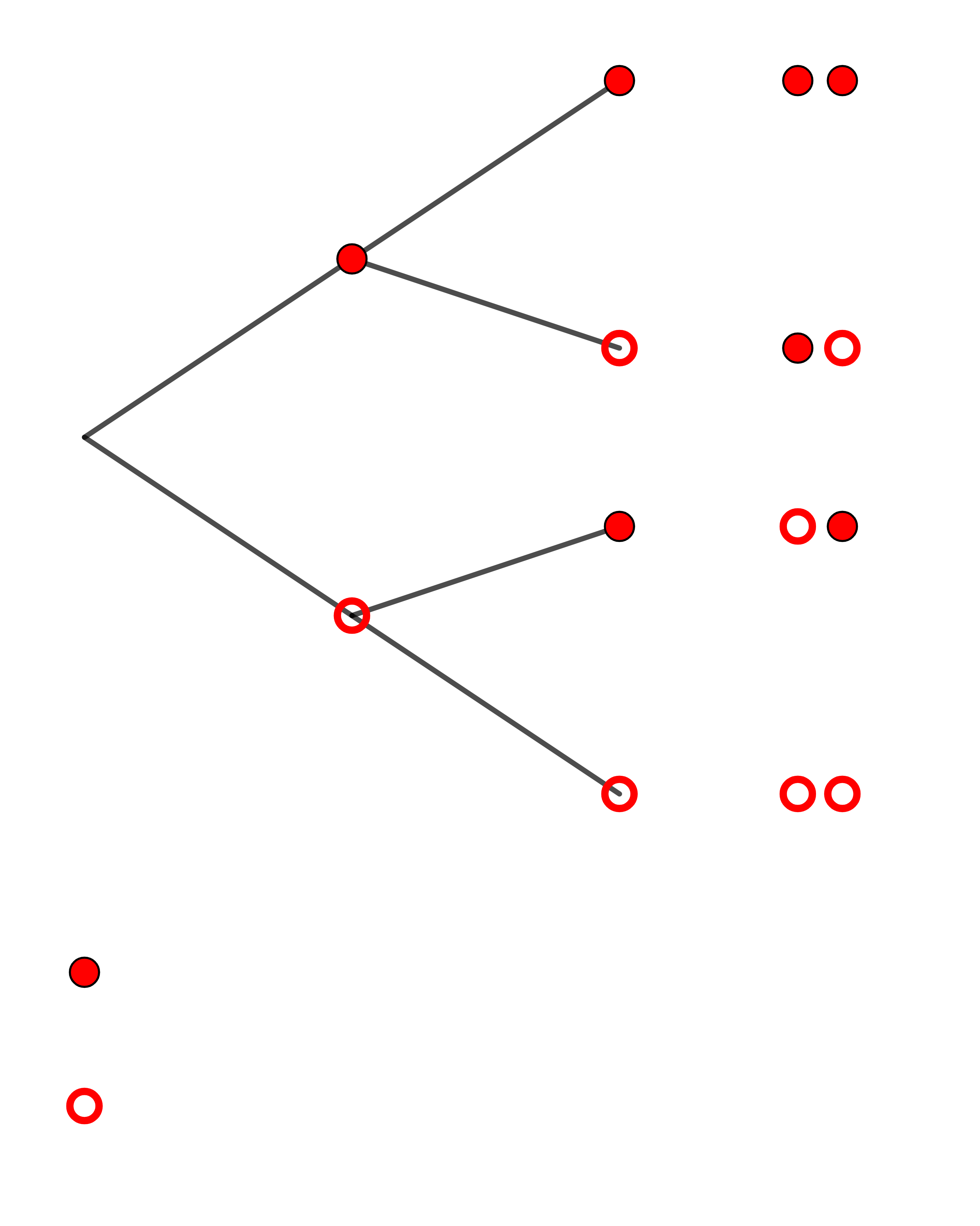
1. Stufe
(1. Drehung)
2. Stufe
(2. Drehung)
Ergebnis
Wahrscheinlichkeit
=  Treffer (Zeiger auf rotem Feld)
=  Niete (Zeiger nicht auf rotem Feld)
P(E)  =  
Kontrolle
Lösung
4. ← → 6.