6. Zufallsgröße und Wahrscheinlichkeitsverteilung

← Kapitelübersicht
Eine Zufallsgröße ist eine Funktion, die jedem Ergebnis eines Zufallsversuchs eine reelle Zahl zuordnet. Bei einer Bernoulli-Kette der Länge n gibt die Zufallsgröße X für jedes Ergebnis die Anzahl der Treffer an.

P(X = k) steht für die Wahrscheinlichkeit, dass bei dem n-stufigen Zufallsversuch genau k Treffer vorkommen. Bestimmt man für jeden Wert k, den die Zufallsgröße annehmen kann, die Wahrscheinlichkeit P(X = k), erhält man die sogenannte Wahrscheinlichkeitsverteilung der Zufallsgröße X.
Für das Baumdiagramm zu einer Bernoulli-Kette der Länge 2 aus Kapitel 5 soll nun eine Wahrscheinlichkeitsverteilung der Zufallsgröße X erstellt werden:
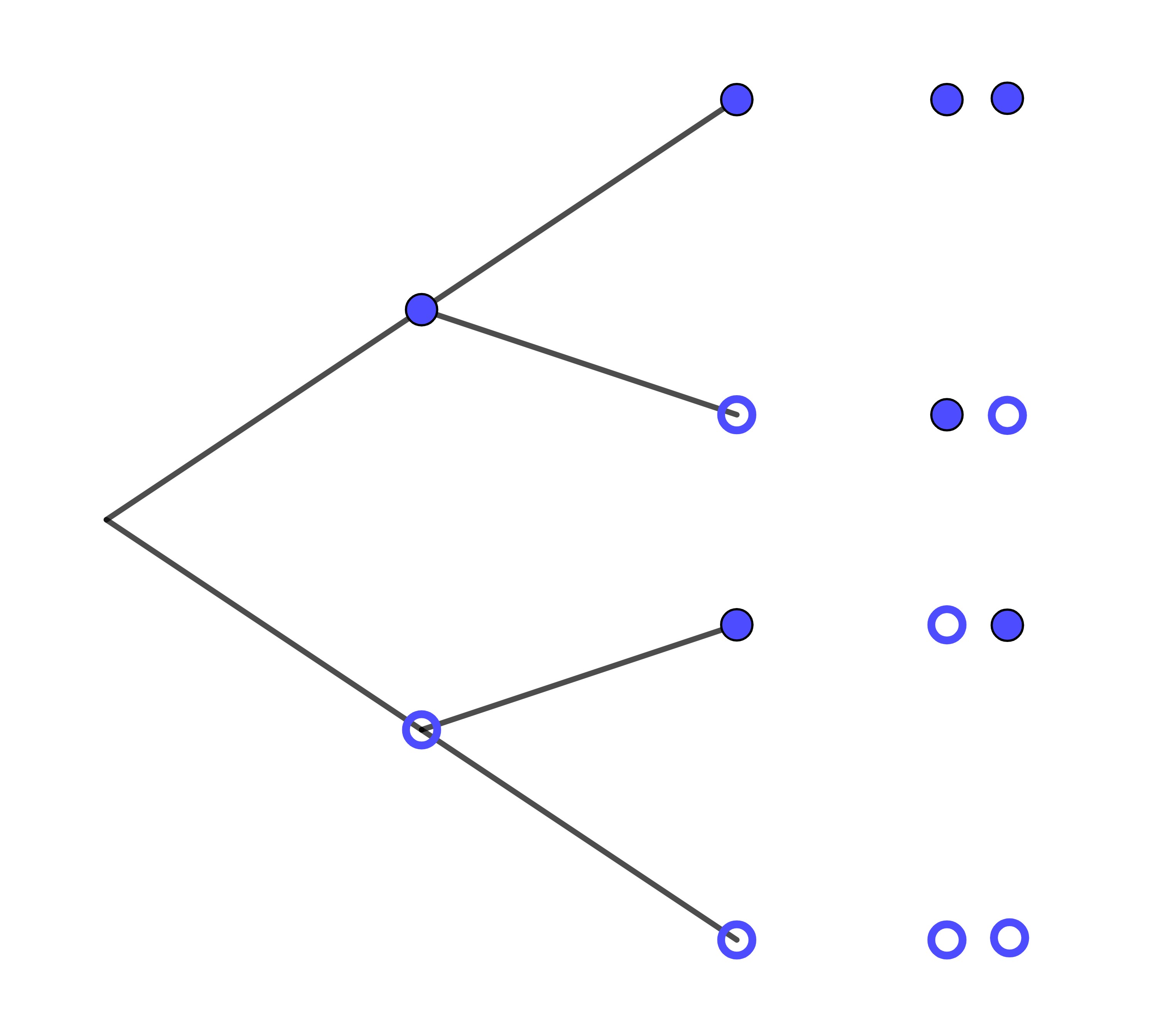
1. Stufe
(1. Drehung)
2. Stufe
(2. Drehung)
Ergebnis
Wahrscheinlichkeit
Zufallsgröße X
(Anzahl der Treffer)
Wahrscheinlichkeitsverteilung
1
4
3
4
1
4
3
4
1
4
3
4
1
4
  ·  
1
4
  =  
1
16
1
4
  ·  
3
4
  =  
3
16
3
4
  ·  
1
4
  =  
3
16
3
4
  ·  
3
4
  =  
9
16
X = 2
X = 1
X = 1
X = 0
P(X = 2)  =  
1
16
P(X = 1)  =  
3
16
  +  
3
16
  =  
6
16
P(X = 0)  =  
9
16
Die Wahrscheinlichkeitsverteilung der Zufallsgröße X kann mithilfe einer Tabelle übersichtlich dargestellt werden:
k  0  1  2
P(X = k)
9
16
6
16
1
16
Übung:
Aus einem Skatkartenspiel wird zweimal hintereinander eine Karte gezogen. Nach jedem Ziehen wird die Karte zurückgelegt und das Kartenspiel neu gemischt. Als Treffer soll gelten: Die gezogene Karte ist eine Dame.

Füllen Sie für das nachfolgende Baumdiagramm und die anschließende Wahrscheinlichkeitsverteilung der Zufallsgröße X alle Eingabefelder aus und kontrollieren Sie ihre Ergebnisse.
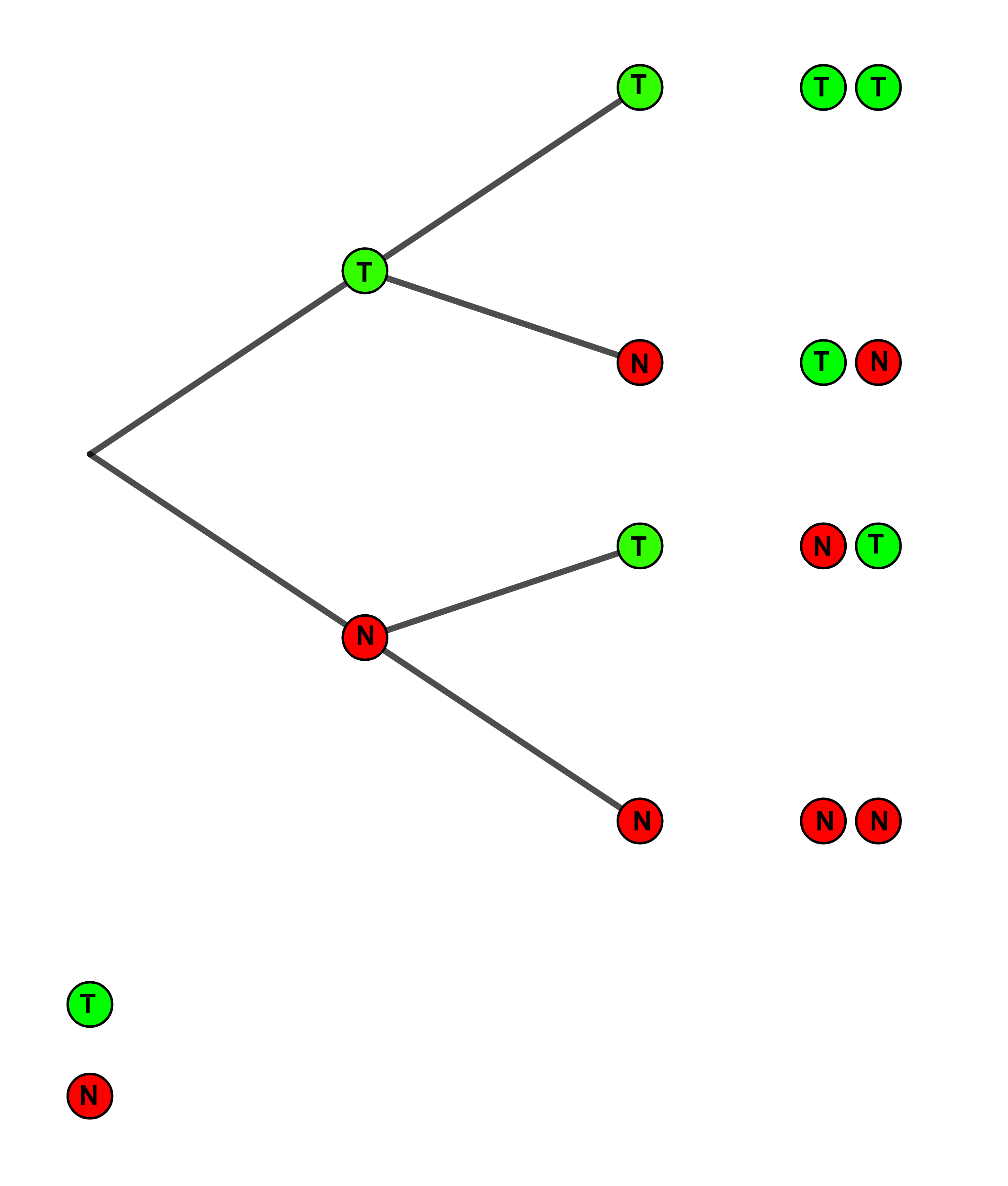
1. Stufe
(1. Drehung)
2. Stufe
(2. Drehung)
Ergebnis
Wahrscheinlichkeit
Zufallsgröße X
(Anzahl der Treffer)
X  =  
X  =  
X  =  
X  =  
=  Treffer
=  Niete
k  0  1  2
P(X = k)
Kontrolle
Lösung
5. ← → 7.