7. Binomialverteilung für eine Bernoulli-Kette der Länge 3
← KapitelübersichtDie Wahrscheinlichkeitsverteilung der Zufallsgröße X, die die Anzahl der Treffer bei einer Bernoulli-Kette angibt, wird Binomialverteilung genannt.
Nachfolgend ist ein typisches Baumdiagramm zu einer Bernoulli-Kette der Länge n = 3 mit der Wahrscheinlichkeit p für einen Treffer und der Wahrscheinlichkeit q = 1 - p für eine Niete abgebildet:
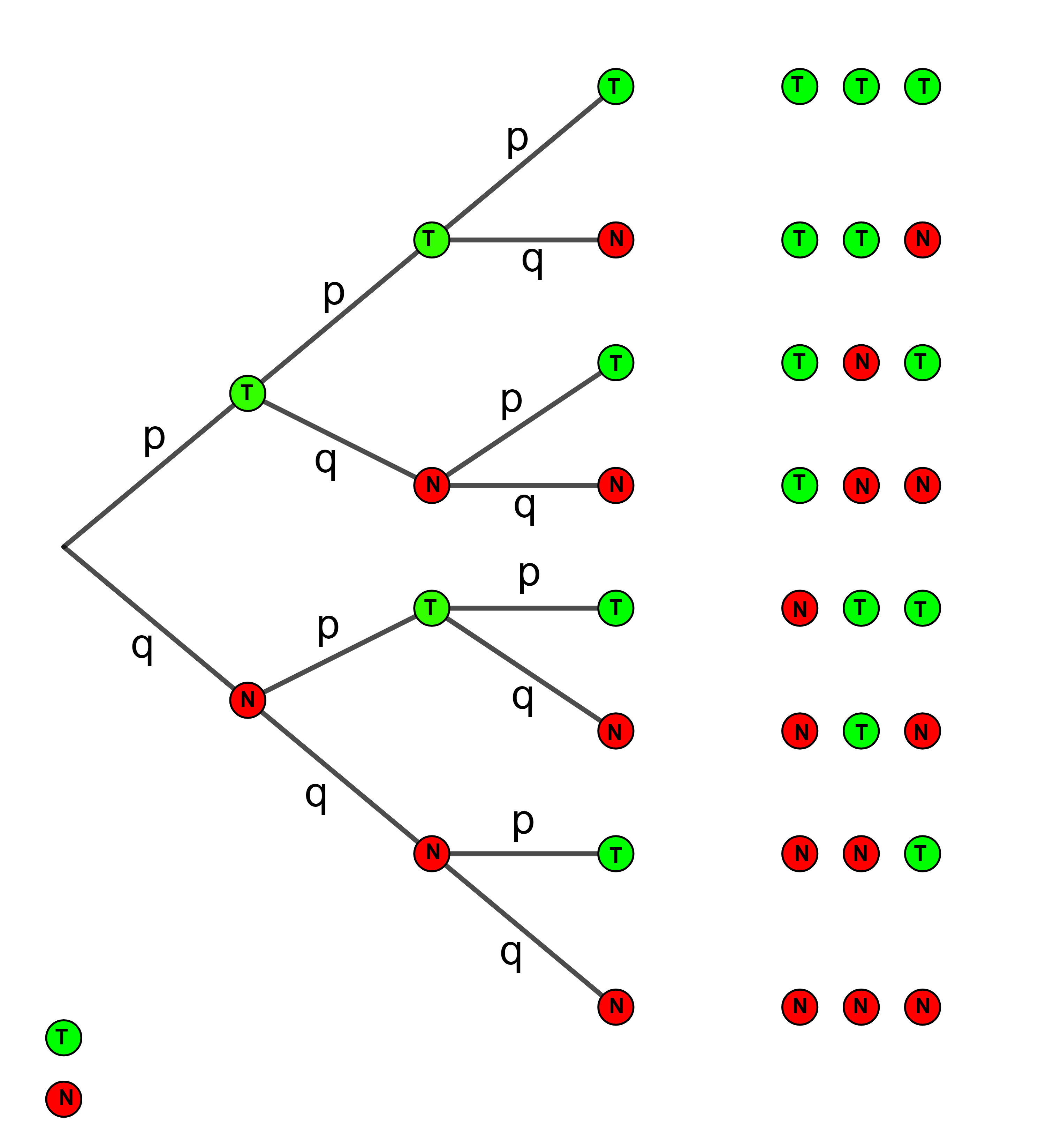
1. Stufe
2. Stufe
3. Stufe
Ergebnis
Wahrscheinlichkeit
Zufallsgröße X
(Anzahl der Treffer)
(Anzahl der Treffer)
p ⋅ p ⋅ p = p3
p ⋅ p ⋅ q = p2 ⋅ q
p ⋅ q ⋅ p = p2 ⋅ q
p ⋅ q ⋅ q = p ⋅ q2
q ⋅ p ⋅ p = p2 ⋅ q
q ⋅ p ⋅ q = p ⋅ q2
q ⋅ q ⋅ p = p ⋅ q2
q ⋅ q ⋅ q = q3
X = 3
X = 2
X = 2
X = 1
X = 2
X = 1
X = 1
X = 0
= Treffer
= Niete
Man erkennt: Es gibt drei Ergebnisse mit X = 2. Alle haben dieselbe Wahrscheinlichkeit p2 ⋅ q.
Deshalb gilt: P(X = 2) = 3 ⋅ p2 ⋅ q.
Ebenso gibt es drei Ergebnisse mit X = 1. Alle haben die Wahrscheinlichkeit p ⋅ q2.
Deshalb gilt: P(X = 1) = 3 ⋅ p ⋅ q2.
Die nachfolgende Tabelle gibt die Binomialverteilung für eine Bernoulli-Kette der Länge n = 3 an.
Deshalb gilt: P(X = 2) = 3 ⋅ p2 ⋅ q.
Ebenso gibt es drei Ergebnisse mit X = 1. Alle haben die Wahrscheinlichkeit p ⋅ q2.
Deshalb gilt: P(X = 1) = 3 ⋅ p ⋅ q2.
Die nachfolgende Tabelle gibt die Binomialverteilung für eine Bernoulli-Kette der Länge n = 3 an.
| k | 0 | 1 | 2 | 3 |
| P(X = k) | q3 | 3 ⋅ p ⋅ q2 | 3 ⋅ p2 ⋅ q | p3 |
Übung:
Erstellen Sie die Binomialverteilung für die Trefferwahrscheinlichkeit p =
| 1 |
| 4 |
.
| k | 0 | 1 | 2 | 3 | ||||||||||||||||||||
| P(X = k) |
(
)3 =
|
3 ⋅
⋅
(
)2 =
|
3 ⋅
(
)2
⋅
=
|
(
)3 =
|
Bestimmen Sie die Wahrscheinlichkeit des Ereignisses E: Es gibt höchstens einen Treffer.
P(E) = P( X ≤
) = P( X =
) + P( X =
) =
+
=