8. Binomialkoeffizienten
← KapitelübersichtDas Baumdiagramm zur Bernoulli-Kette der Länge 3 aus Kapitel 7 hat verdeutlicht, dass alle Ergebnisse mit derselben Anzahl von Treffern dieselbe Wahrscheinlichkeit haben. Um eine Binomialverteilung ohne Baumdiagramm erstellen zu können, muss man in der Lage sein, diese Trefferanzahl zu berechnen.
Bei einer Bernoulli-Kette der Länge n gibt der Binomialkoeffizient
(
| n |
| k |
)
(man liest: n über k) an,
wie viele Ergebnisse des n-stufigen Zufallsversuchs genau k Treffer haben.
Der Binomialkoeffizient wird berechnet mit der Formel:
(
| n |
| k |
)
=
| n! |
| k! ⋅ ( n − k )! |
Der Aufbau des Bruchterms soll nachfolgend an einem Beispiel erklärt werden.

Wie viele Möglichkeiten gibt es, drei verschiedenfarbige Kugeln hintereinander anzuordnen?


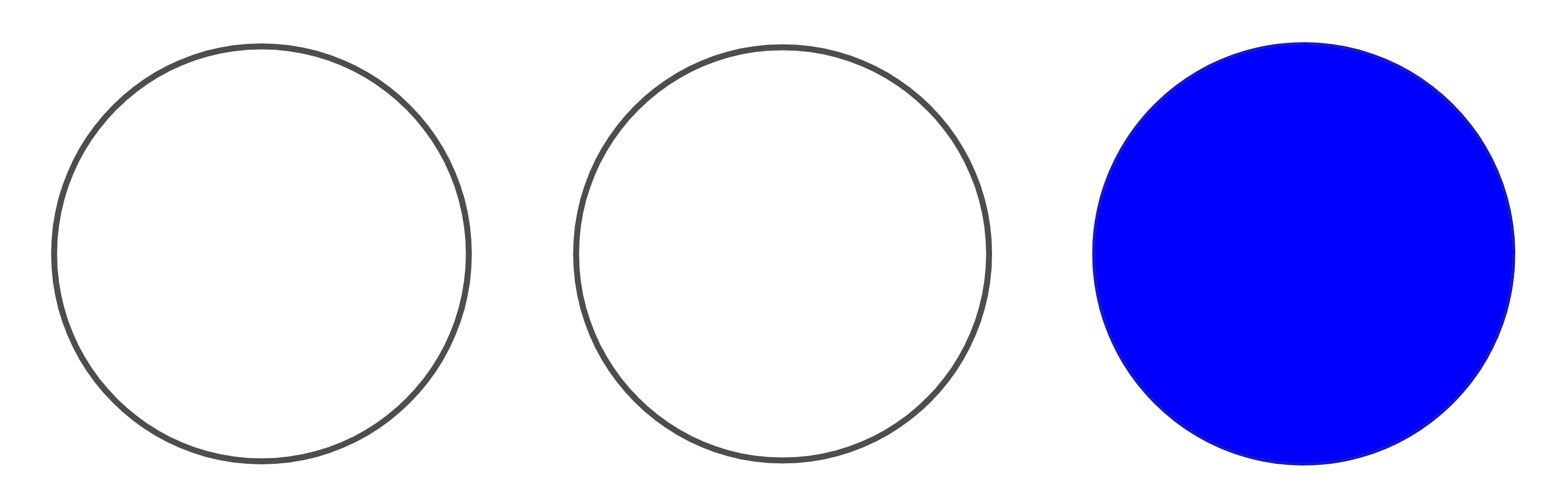
Es gibt 3 mögliche Positionen für die blaue Kugel.

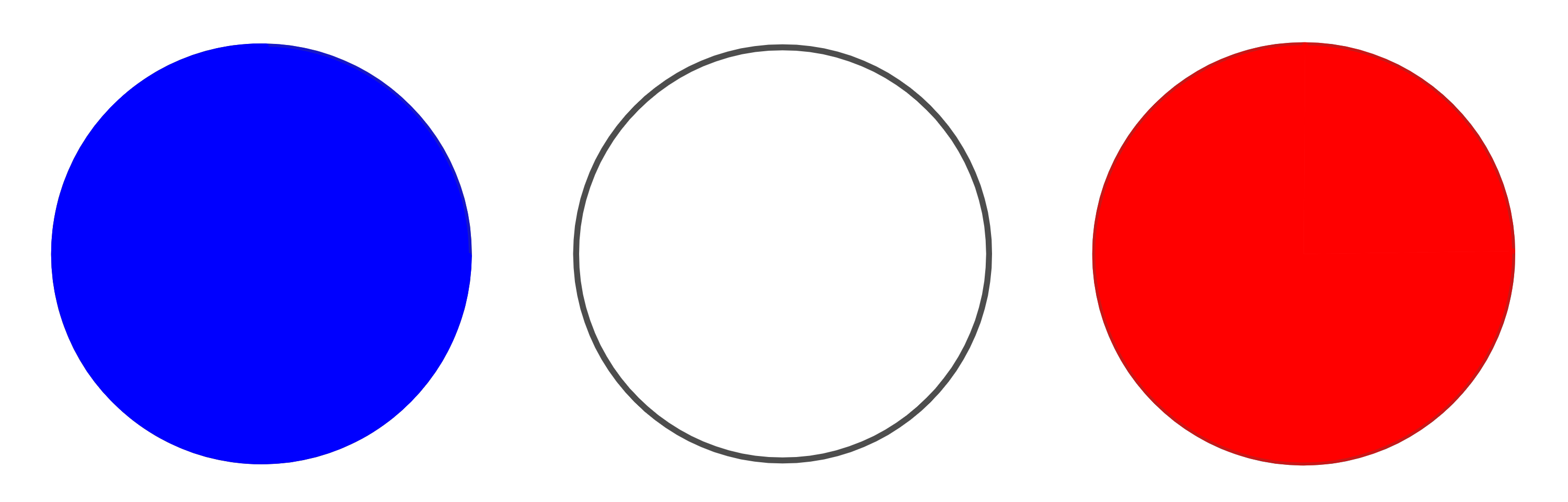




Für die rote Kugel bleiben jeweils 2 mögliche Positionen übrig.






Für die grüne Kugel gibt es nur noch jeweils 1 mögliche Position.
Es gibt also 3 ⋅ 2 ⋅ 1 = 6 Möglichkeiten, drei verschiedene Objekte nacheinander anzuordnen.
Diese Zahl wird 3 Fakultät genannt und mit 3! bezeichnet. 3! ist das Produkt aller positiven ganzen Zahlen von 1 bis 3.
Diese Zahl wird 3 Fakultät genannt und mit 3! bezeichnet. 3! ist das Produkt aller positiven ganzen Zahlen von 1 bis 3.
n! (man liest: n Fakultät) ist das Produkt aller positiven ganzen Zahlen von 1 bis n.
n! = 1 ⋅ 2 ⋅ . . . ⋅ n
Mit n! berechnet man die Anzahl der Möglichkeiten, n verschiedene Objekte nacheinander anzuordnen.
n! = 1 ⋅ 2 ⋅ . . . ⋅ n
Mit n! berechnet man die Anzahl der Möglichkeiten, n verschiedene Objekte nacheinander anzuordnen.
Nehmen wir jetzt an, der Binomialkoeffizient
(
| 5 |
| 3 |
)
soll ermittelt werden.
Er gibt an, wie viele der möglichen Ergebnisse einer Bernoulli-Kette der Länge n = 5 genau 3 Treffer haben. Jeder Pfad des zugehörigen Baumdiagramms hat 5 Stufen. Die Treffer T1, T2 und T3 können auf diesen Stufen unterschiedliche Positionen einnehmen.
Für Treffer T1 gibt es 5 mögliche Positionen:
| T1 |
| T1 |
| T1 |
| T1 |
| T1 |
Für Treffer T2 bleiben jeweils 4 mögliche Positionen übrig, zum Beispiel:
| T1 | T2 |
| T1 | T2 |
| T1 | T2 |
| T1 | T2 |
Treffer T3 hat dann noch jeweils 3 mögliche Positionen zur Auswahl, zum Beispiel:
| T1 | T2 | T3 |
| T1 | T2 | T3 |
| T1 | T2 | T3 |
Es gibt also 5 ⋅ 4 ⋅ 3 = 60 Möglichkeiten, 3 Treffer auf 5 Stufen zu verteilen, wenn man die Nummerierung der Treffer beachtet. Diese spielt jedoch keine Rolle.
Von den 60 Möglichkeiten gehören jeweils sechs zum selben Ergebnis der Bernoulli-Kette, zum Beispiel: Treffer auf den ersten drei Stufen.
Von den 60 Möglichkeiten gehören jeweils sechs zum selben Ergebnis der Bernoulli-Kette, zum Beispiel: Treffer auf den ersten drei Stufen.
| T1 | T2 | T3 |
| T1 | T3 | T2 |
| T2 | T1 | T3 |
| T3 | T1 | T2 |
| T2 | T3 | T1 |
| T3 | T2 | T1 |
Hier liegt eine Vertauschung von 3 Objekten vor.
Anzahl = 3! = 6
Anzahl = 3! = 6
Um die tatsächliche Anzahl von Ergebnissen mit genau 3 Treffern zu ermitteln, muss man also noch 60 durch 6 dividieren. Somit erhält man die Gleichung:
(
| 5 |
| 3 |
)
=
| 5 ⋅ 4 ⋅ 3 |
| 3! |
=
| 60 |
| 6 |
= 10
Eine Bernoulli-Kette der Länge 5 hat also 10 Ergebnisse mit genau 3 Treffern. Um auf die oben genannte Formel für den Binomialkoeffizienten zu kommen, muss man den Bruchterm noch erweitern:
(
| 5 |
| 3 |
)
=
| 5 ⋅ 4 ⋅ 3 |
| 3! |
=
| 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 |
| 3! ⋅ 2 ⋅ 1 |
=
| 5! |
| 3! ⋅ 2! |
=
| 5! |
| 3! ⋅ (5 − 3)! |
Übung:
Berechnen Sie die nachfolgenden Binomialkoeffizienten mit Hilfe der im gelben Kasten angegebenen Formel. Kürzen Sie den Bruchterm, bevor Sie das Ergebnis berechnen.
Beachten Sie: 0! = 1
Beachten Sie: 0! = 1
(
| 5 |
| 0 |
)
=
| 5! |
| ! ⋅ ( 5 − ) ! |
=
| 5! |
| ! ⋅ ! |
=
| 1 ⋅ ⋅ ⋅ ⋅ |
| 1 ⋅ 1 ⋅ ⋅ ⋅ ⋅ |
=
=
(
| 5 |
| 1 |
)
=
| ! |
| ! ⋅ ( − ) ! |
=
| ! |
| ! ⋅ ! |
=
| 1 ⋅ ⋅ ⋅ ⋅ |
| 1 ⋅ 1 ⋅ ⋅ ⋅ |
=
=
(
| 5 |
| 2 |
)
=
| ! |
| ! ⋅ ( − ) ! |
=
| ! |
| ! ⋅ ! |
=
| 1 ⋅ ⋅ ⋅ ⋅ |
| 1 ⋅ ⋅ 1 ⋅ ⋅ |
=
=
(
| 5 |
| 4 |
)
=
| ! |
| ! ⋅ ( − ) ! |
=
| ! |
| ! ⋅ ! |
=
| 1 ⋅ ⋅ ⋅ ⋅ |
| 1 ⋅ ⋅ ⋅ ⋅ 1 |
=
=
(
| 5 |
| 5 |
)
=
| ! |
| ! ⋅ ( − ) ! |
=
| ! |
| ! ⋅ ! |
=
| 1 ⋅ ⋅ ⋅ ⋅ |
| 1 ⋅ ⋅ ⋅ ⋅ ⋅ 1 |
=
=
(
| 6 |
| 3 |
)
=
| ! |
| ! ⋅ ( − ) ! |
=
| ! |
| ! ⋅ ! |
=
| 1 ⋅ ⋅ ⋅ ⋅ ⋅ |
| 1 ⋅ ⋅ ⋅ 1 ⋅ ⋅ |
=
=
(
| 7 |
| 2 |
)
=
| ! |
| ! ⋅ ( − ) ! |
=
| ! |
| ! ⋅ ! |
=
| 1 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ |
| 1 ⋅ ⋅ 1 ⋅ ⋅ ⋅ ⋅ |
=
=