Jedes bestimmte Integral der Form
b
∫
f(x) dx
hat einen bestimmten Wert.
a
Ist a < b, hat der Integralwert eine geometrische Bedeutung. Diese wird nachfolgend an einem Beispiel erklärt.
Geometrische Bedeutung des Integralwertes
← ThemenübersichtDer Wert des Integrals
6
∫
f(x)
dx
-1
soll für die Funktion f mit f(x) = 0,1x3 - 0,4x2 - 0,7x + 1 geometrisch ermittelt werden.
Dazu wird nur der Abschnitt auf dem Graphen der Funktion f betrachtet, der zwischen den Integrationsgrenzen, also im Intervall [-1 ; 6] liegt.
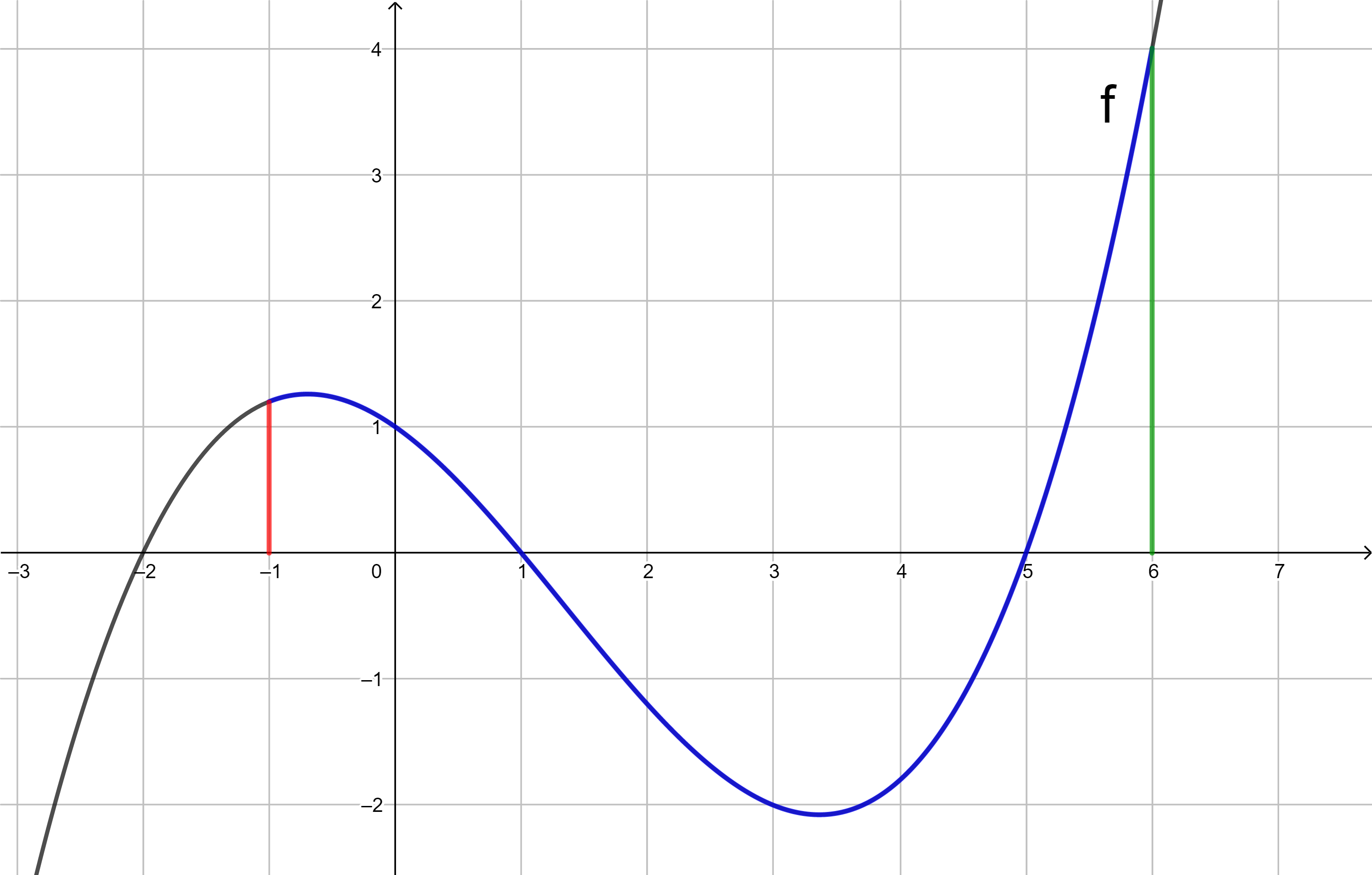
Der Graph von f begrenzt im Intervall [-1 ; 6] mit der x‑Achse drei Flächenstücke, die entweder oberhalb oder unterhalb der x‑Achse liegen. In der nachfolgenden Zeichnung sind die jeweiligen Flächeninhalte (in FE = Flächeneinheiten) angegeben.
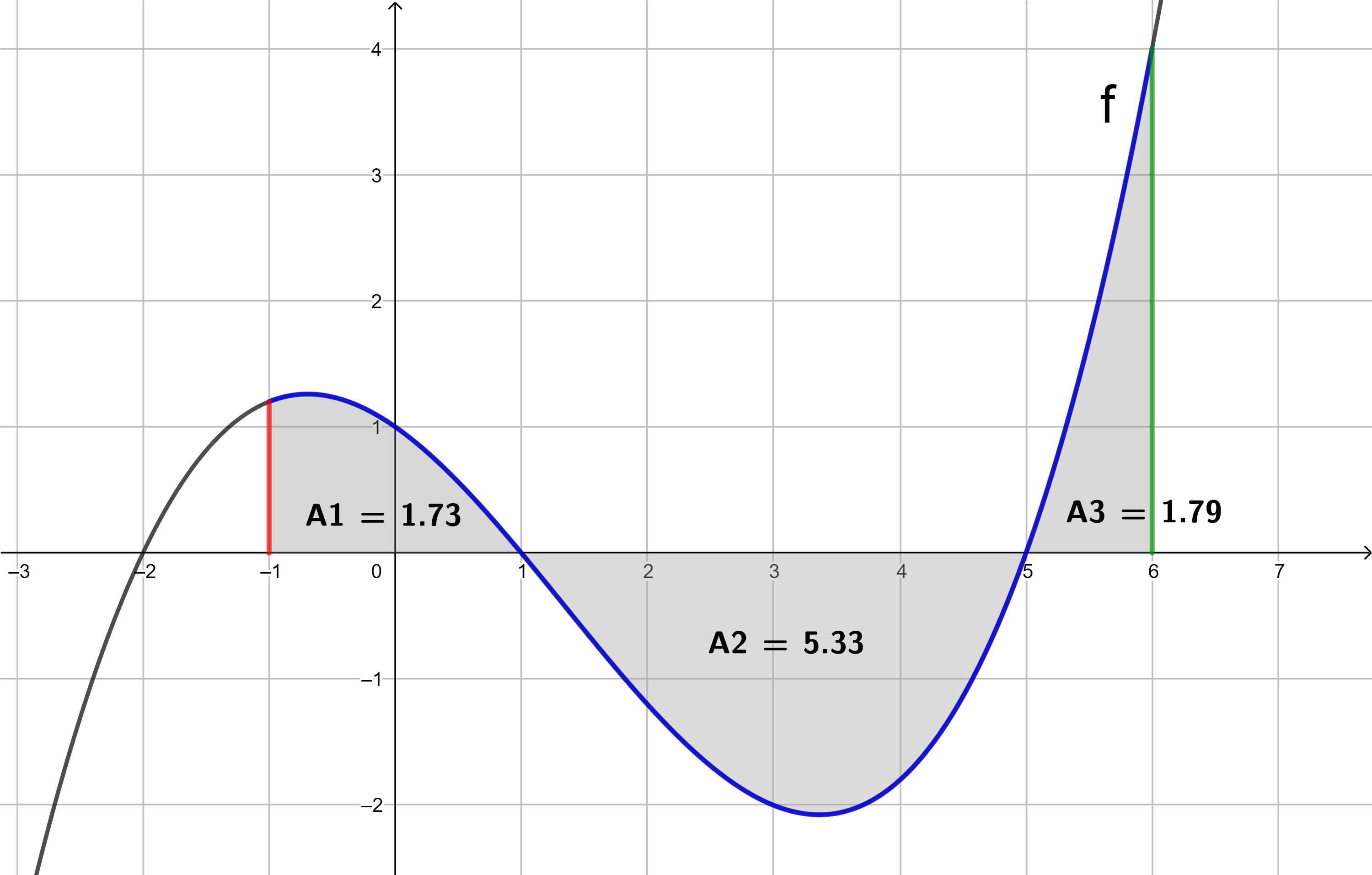
Für die geometrische Bestimmung des Integralwertes benötigt man den Begriff des "orientierten Flächeninhalts". Liegt die Fläche oberhalb der x‑Achse, ist der orientierte Flächeninhalt positiv, liegt die Fläche unterhalb der x‑Achse, ist er negativ. Die nachfolgende Tabelle zeigt den tatsächlichen Flächeninhalt und den orientierten Flächeninhalt für die drei Flächenstücke im Vergleich.
| A1 | A2 | A3 | |
| Flächeninhalt in FE | 1,73 | 5,33 | 1,79 |
| orientierter Flächeninhalt | 1,73 | -5,33 | 1,79 |
Der Wert des Integrals
6
∫
f(x)
dx
-1
entspricht der Summe der orientierten Flächeninhalte aller Flächenstücke im Intervall [-1 ; 6].
6
∫
f(x)
dx = 1,73 + (-5,33) + 1,79 = -1,81
-1
Hinweis:
Der Integralwert ist negativ, weil die Fläche, die unterhalb der x‑Achse liegt, größer ist als die gesamte Fläche oberhalb der x‑Achse.
Der Integralwert ist negativ, weil die Fläche, die unterhalb der x‑Achse liegt, größer ist als die gesamte Fläche oberhalb der x‑Achse.
Übung zur geometrischen Bestimmung von Integralwerten:
Klicken Sie
hier
, um eine neue Aufgabe zu erzeugen.
Bestimmen Sie für die unten abgebildete Funktion f den Wert des Integrals
6
∫
f(x)
dx.
-1
Wählen Sie die Flächenstücke aus, deren orientierten Flächeninhalt Sie für die Bestimmung des Integralwertes benötigen:
Füllen Sie die Eingabefelder aus und kontrollieren Sie Ihr Ergebnis. Ersetzen Sie (wie in der Zeichnung) das Komma in einer Dezimalzahl durch einen Punkt. Achten Sie auf die Klammersetzung bei negativen Summanden.
6
∫
f(x)
dx =
-1
+
+
+
=