Bestimmung von Stammfunktionen
← ThemenübersichtZu jeder Funktion kann man Ableitungsfunktionen bestimmen.
Die Funktion f mit f(x) = 3x2 - 12x hat die Ableitungsfunktion f ' mit f '(x) = 6x - 12.
Die Funktion f ' hat die Ableitungsfunktion f '' mit f ''(x) = 6.
Kann man umgekehrt zur Funktion f eine Funktion F finden, für die f die Ableitungsfunktion ist?
Ja, dies gilt zum Beispiel für die Funktion F mit F(x) = x3 - 6x2, denn
F '(x) = 3 ⋅ x3 - 1 - 6 ⋅ 2 ⋅ x2 - 1 = 3x2 - 12x = f(x).
Jede Funktion F, für die F '(x) = f(x) gilt, heißt Stammfunktion von f. Stammfunktionen werden in der Regel mit Großbuchstaben bezeichnet.
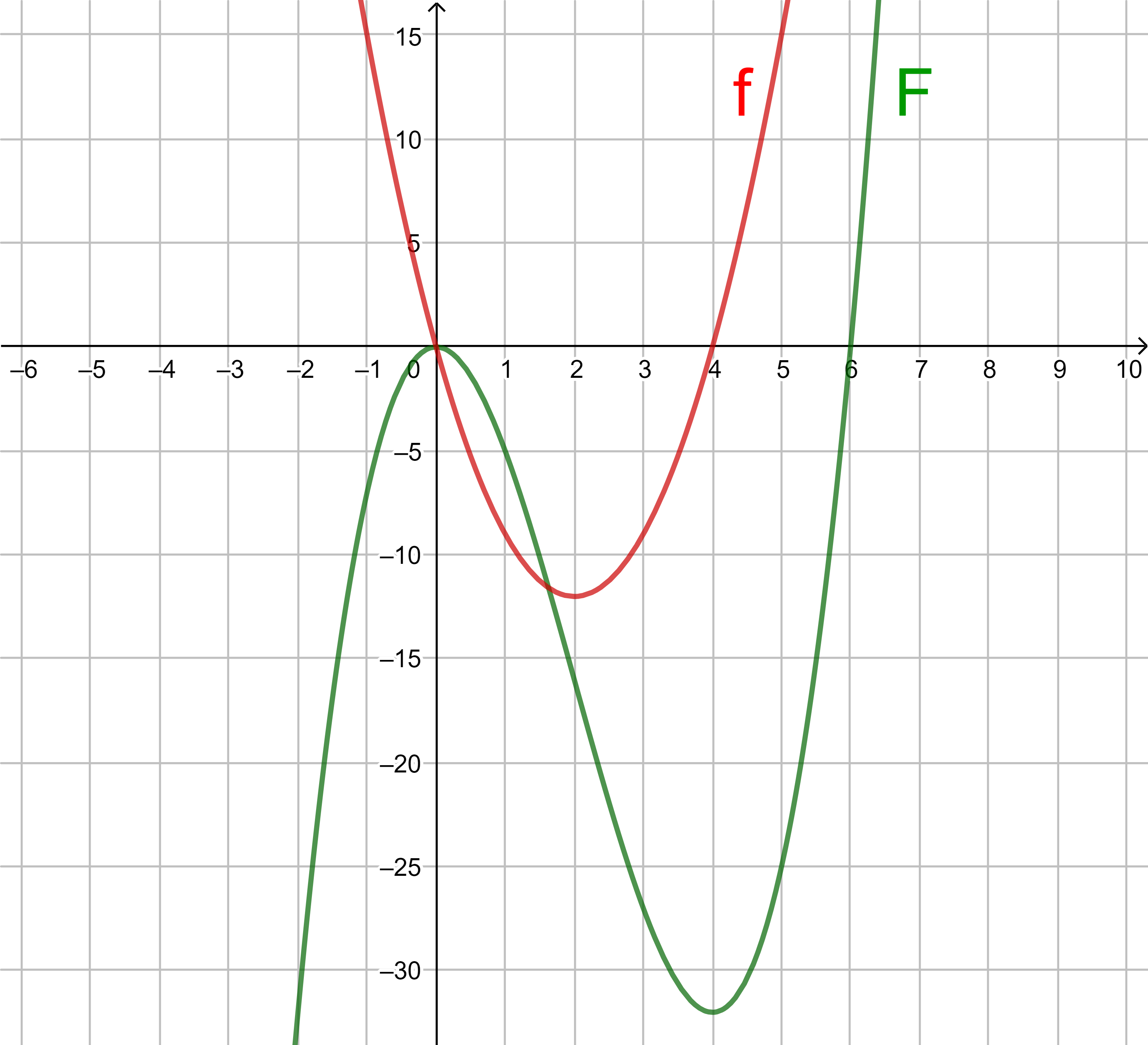
Der Funktionswert f(x) gibt die Steigung von F an der Stelle x an.
Man erkennt dies in der Grafik zum Beispiel daran, dass der Graph von f an den lokalen Extremstellen von F die x-Achse schneidet.
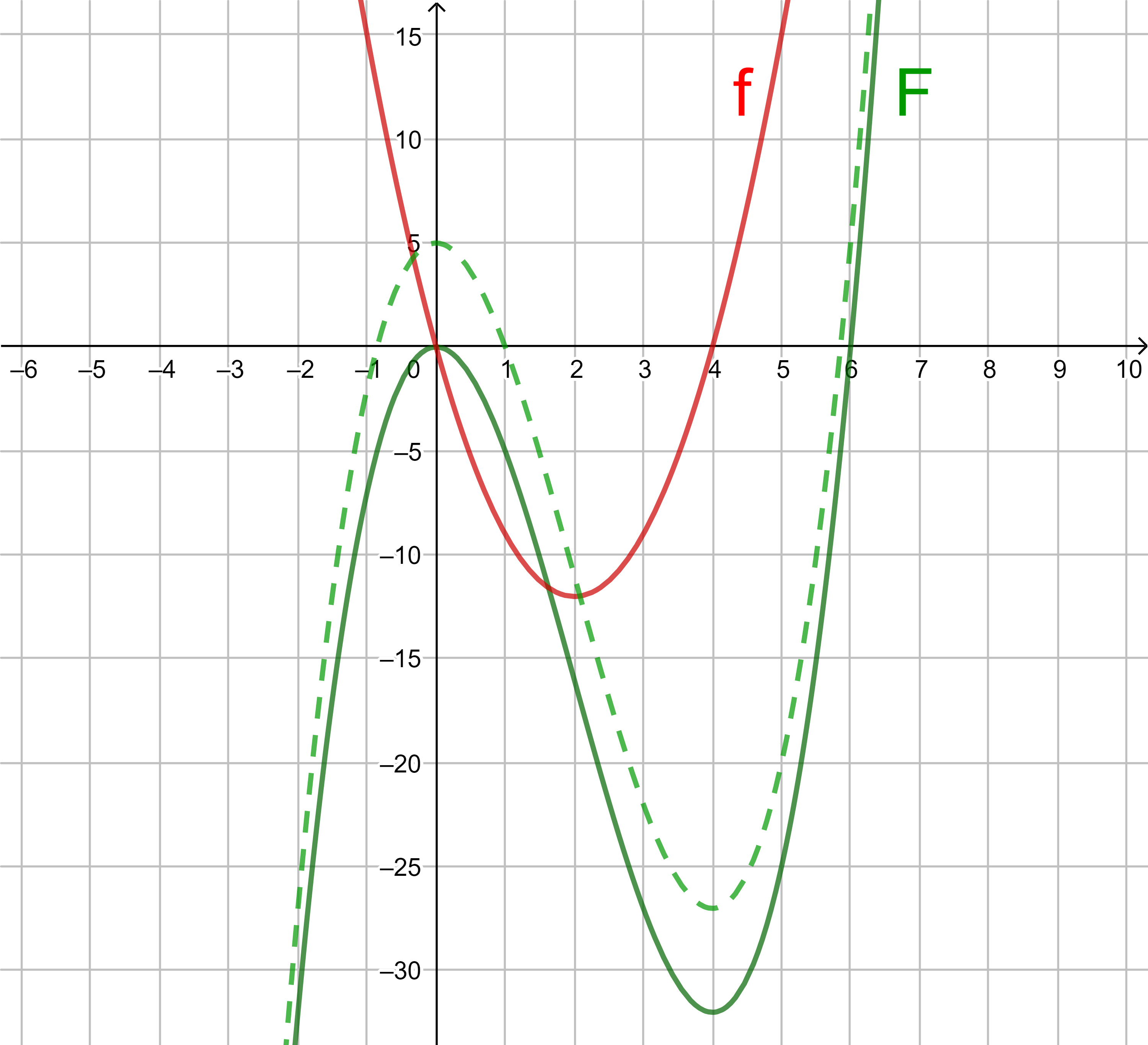
Verschiebt man den Graphen von F in y-Richtung nach oben oder unten, ändert sich dadurch die Steigung von F an einer beliebigen Stelle x nicht.
Auch die Funktion F mit F(x) = x3 - 6x2 + 5 hat die Ableitung F '(x) = 3x2 - 12x = f(x), ist also eine Stammfunktion von f.
Für jede reelle Zahl c ist die Funktion F mit F(x) = x3 - 6x2 + c eine Stammfunktion von f.
Allgemein gilt: Hat man zu einer Funktion f eine Stammfunktion F gefunden, erhält man weitere Stammfunktionen, indem man zum Funktionsterm F(x) eine beliebige reelle Zahl c addiert.
Für die Berechnung von Integralwerten mit dem Hauptsatz (siehe nächstes Kapitel) genügt es, eine beliebige Stammfunktion von f zu kennen. Der Wert von c hat keinen Einfluss auf das Ergebnis der Berechnung.
Für die Bestimmung einer Stammfunktion zu einer ganzrationalen Funktion gibt es drei einfache Regeln. Sie entsprechen den Regeln für das Ableiten ganzrationaler Funktionen. Da das Stammfunktionbilden sozusagen die Umkehrung des Ableitens ist, nennt man es auch "aufleiten".
Potenzregel:
Eine Stammfunktion der Potenzfunktion f mit f(x) = xn (n = 1, 2, 3, ...) ist F mit F(x) =
| 1 |
| n + 1 |
· xn + 1.
Beispiel:
Eine Stammfunktion von f(x) = x
5
ist F mit F(x) =
| 1 | |
| 5 | + 1 |
· x
5
+ 1
=
| 1 |
| 6 |
· x
6
,
denn F '(x) =
| 1 |
| 6 |
·
6
· x
5
=
| 6 |
| 6 |
· x
5
= 1· x
5
= x
5
= f(x).
Faktorregel:
Steht vor einer Potenz ein konstanter Faktor, bleibt er beim Aufleiten erhalten.
Beispiel:
Eine Stammfunktion von f(x) =
3
· x
5
ist F mit
F(x) =
3
·
| 1 | |
| 5 | + 1 |
· x
5
+ 1
=
3
·
| 1 |
| 6 |
· x
6
=
| 3 |
| 6 |
· x
6
=
| 1 |
| 2 |
· x
6
Hinweis:
Die Faktorregel gilt auch, wenn der Faktor ein Bruch ist.
Beispiel:
Eine Stammfunktion von f(x) =
| 4 |
| 9 |
· x
7
ist F mit
F(x) =
| 4 |
| 9 |
·
| 1 | |
| 7 | + 1 |
· x
7
+ 1
=
| 4 |
| 9 |
·
| 1 |
| 8 |
· x
8
=
| 4 · 1 |
| 9 · 8 |
· x
8
=
| 4 |
| 72 |
· x
8
=
| 1 |
| 18 |
· x
8
Sonderfall:
Für jede reelle Zahl a ist F mit F(x) = a · x eine Stammfunktion der konstanten Funktion f mit f(x) = a.
Beispiel:
Eine Stammfunktion von f(x) = 5 ist F mit F(x) = 5 · x, eine Stammfunktion von f(x) = -7 ist F mit F(x) = -7 · x.
Summenregel:
Summen (bzw. Differenzen) werden summandenweise aufgeleitet.
Beispiel:
Eine Stammfunktion von f mit
f(x) =
-4
· x
7
+
3
·
x
4
−
6
·
x
2
+
8
ist F mit
F(x) =
-4
·
| 1 | |
| 7 | + 1 |
· x
7
+ 1
+
3
·
| 1 | |
| 4 | + 1 |
· x
4
+ 1
−
6
·
| 1 | |
| 2 | + 1 |
· x
2
+ 1
+
8
· x
=
-4
·
| 1 |
| 8 |
· x
8
+
3
·
| 1 |
| 5 |
· x
5
−
6
·
| 1 |
| 3 |
· x
3
+
8
· x
=
-
| 4 |
| 8 |
· x
8
+
| 3 |
| 5 |
· x
5
−
| 6 |
| 3 |
· x
3
+
8
· x
=
-
| 1 |
| 2 |
· x
8
+
| 3 |
| 5 |
· x
5
−
2
· x
3
+
8
· x
mit Ober- und Untersummen ← → Der Hauptsatz der Differenzial-
und Integralrechnung