Näherungsweise Berechnung von Integralwerten mit Ober- und Untersummen
← ThemenübersichtAufgabe:
Für die Funktion f mit f(x) = 0,2x2 - 1,4x + 1,2 soll der Wert des Integrals
3
∫
f(x)
dx
1,8
näherungsweise ermittelt werden.
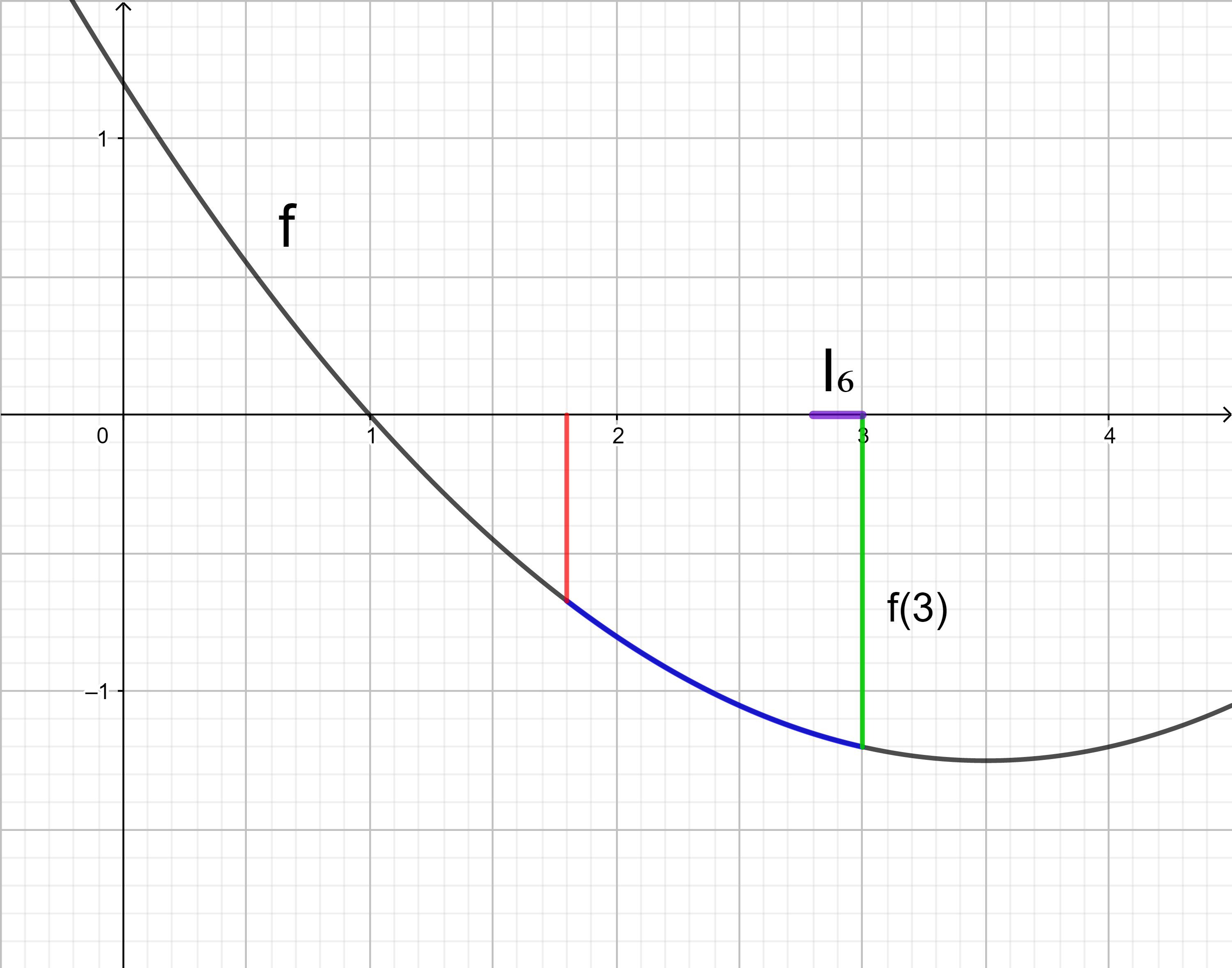
Der Wert des gesuchten Integrals entspricht dem orientierten Flächeninhalt der schraffierten Fläche. Da die Fläche unterhalb der x‑Achse liegt, ist der orientierte Flächeninhalt negativ. Der Wert des Integrals und der tatsächliche Flächeninhalt der schraffierten Fläche haben entgegengesetzte Vorzeichen.
(→ Geometrische Bedeutung des Integralwertes)
Die Rechtecke, die zu den Unter- und Obersummen, mit denen der Integralwert näherungsweise ermittelt werden kann, gehören, liegen ebenfalls unterhalb der x-Achse. Deshalb ist auch der orientierte Flächeninhalt der Rechtecke negativ.
Nachfolgend soll die Untersumme U3 bestimmt werden. Sie ist kleiner als der gesuchte Integralwert.
Die Strecke zwischen den Integrationsgrenzen, also zwischen 1,8 und 3, wird in drei gleiche Teile geteilt.
(3 - 1,8) : 3 = 1,2 : 3 = 0,4
Jedes Rechteck hat die Breite 0,4 (LE = Längeneinheiten).
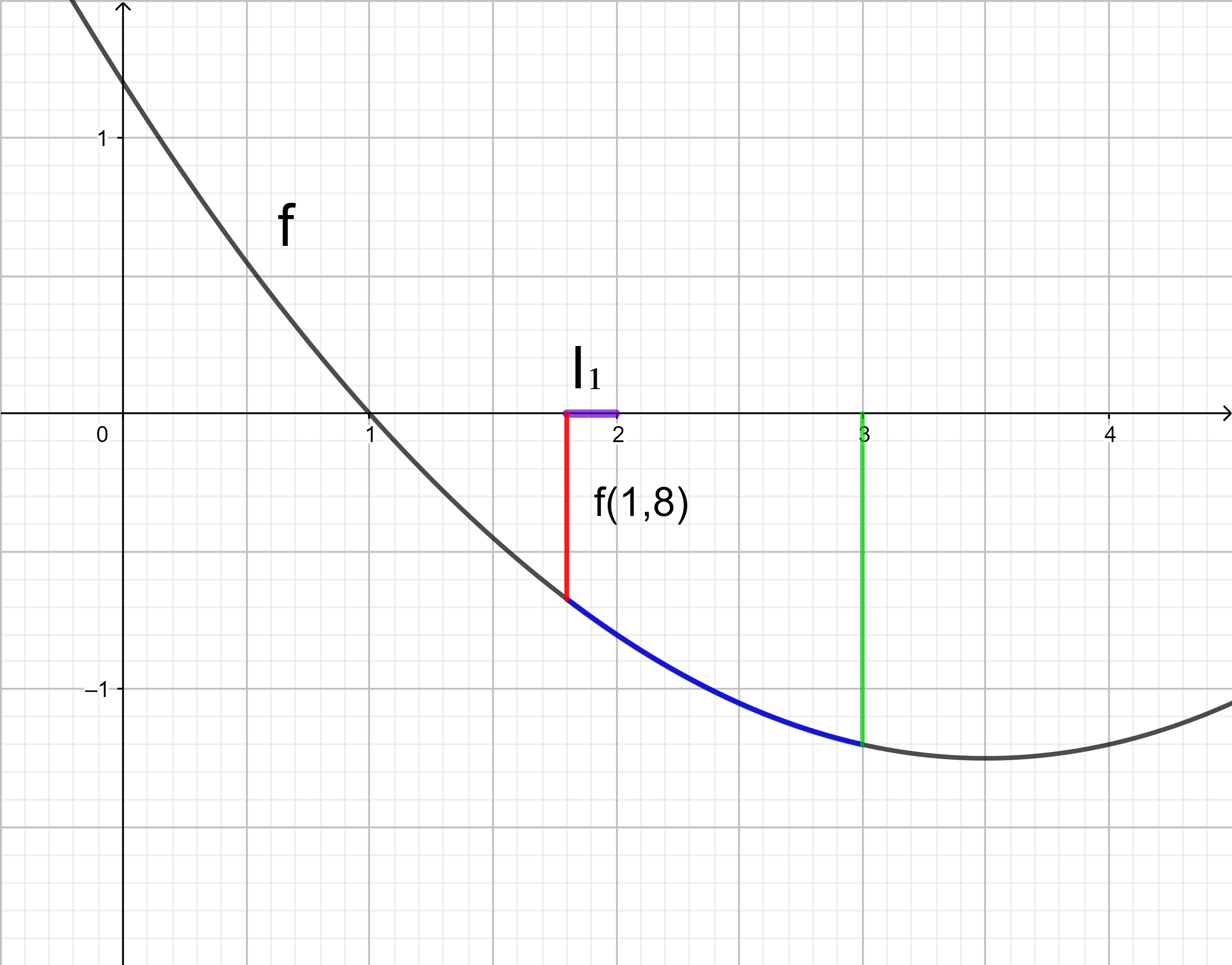
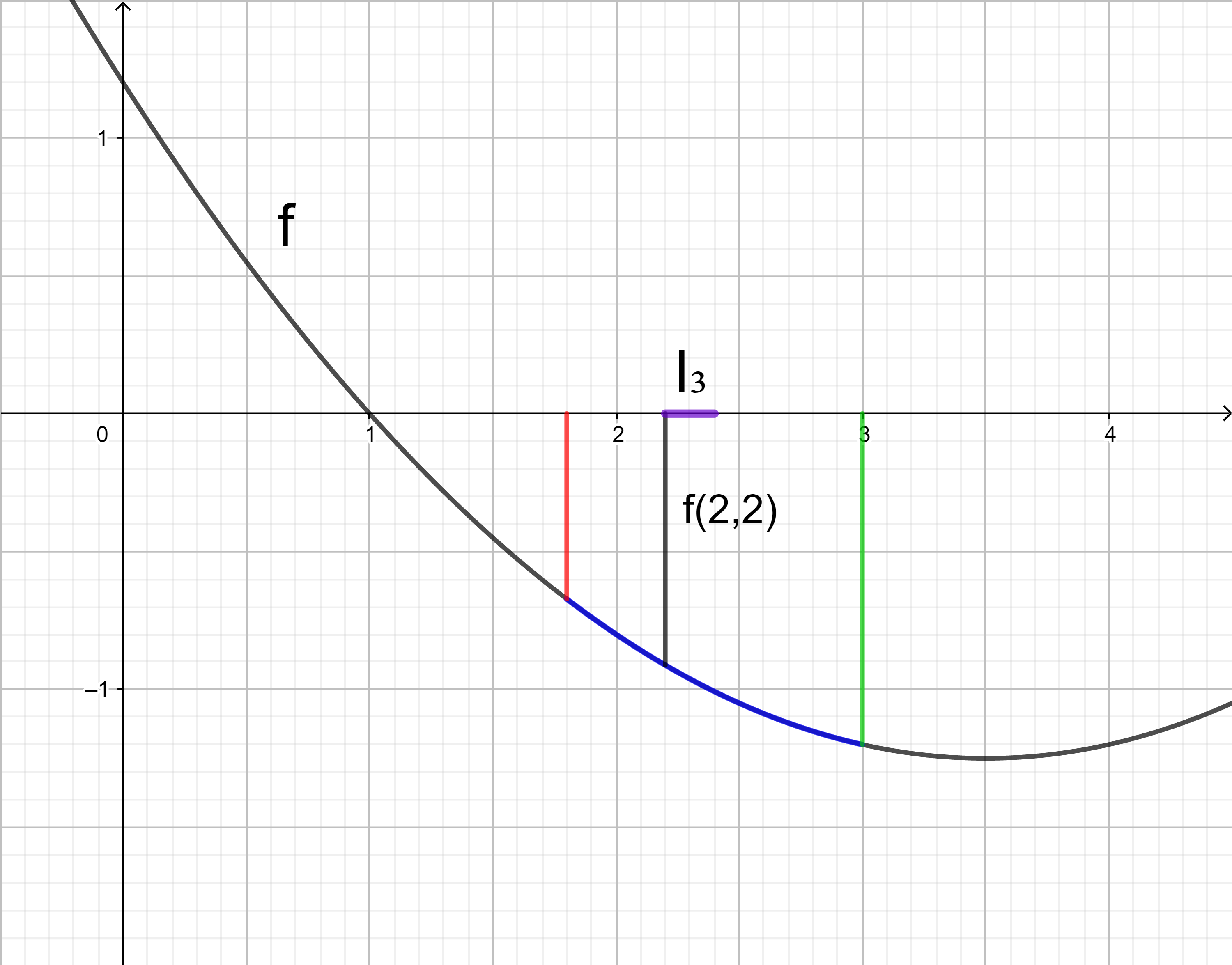
Das Intervall [1,8 ; 3] wird in drei Teilintervalle I1, I2, und I3 unterteilt, zu denen jeweils ein Rechteck gehört.
(3 - 1,8) : 3 = 1,2 : 3 = 0,4
Jedes Rechteck hat die Breite 0,4 (LE = Längeneinheiten).
Das Intervall [1,8 ; 3] wird in drei Teilintervalle I1, I2, und I3 unterteilt, zu denen jeweils ein Rechteck gehört.
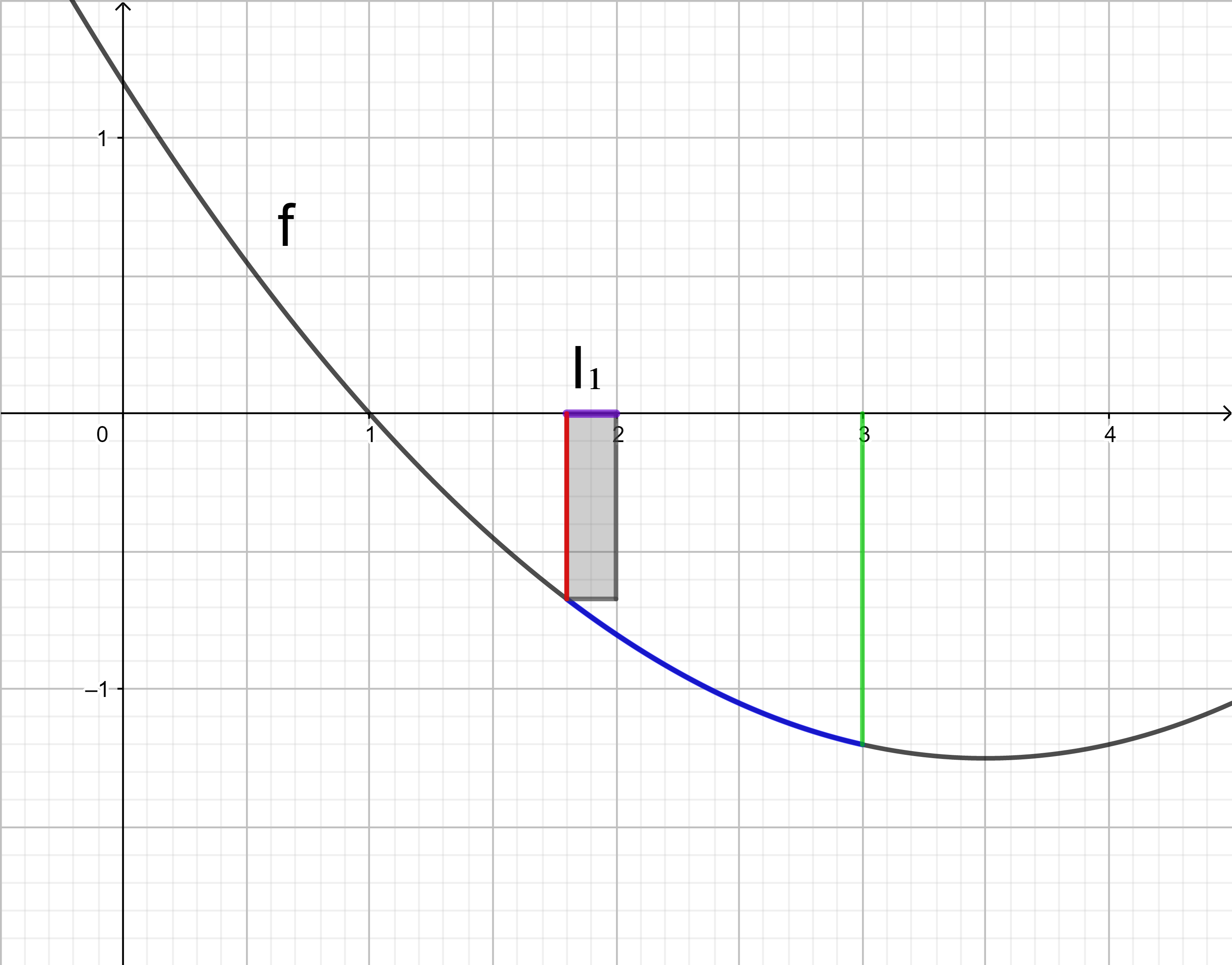
Da die Untersumme U3 kleiner als der gesuchte Integralwert sein soll, wird in jedem Teilintervall I1, I2, I3 der kleinste Funktionswert gesucht und anschließend ein Rechteck mit der Breite 0,4 und dem Betrag des kleinsten Funktionswerts als Länge gezeichnet.
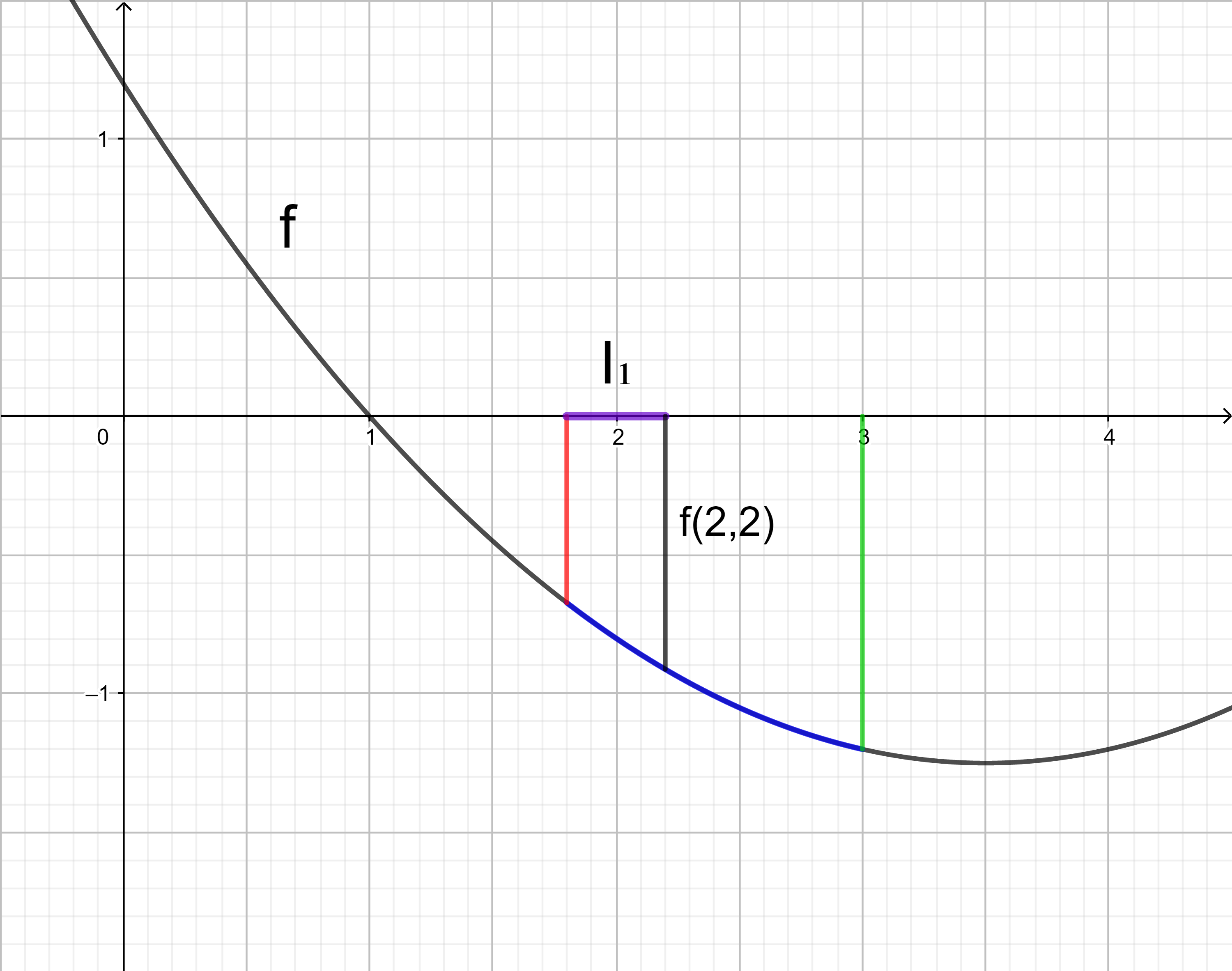
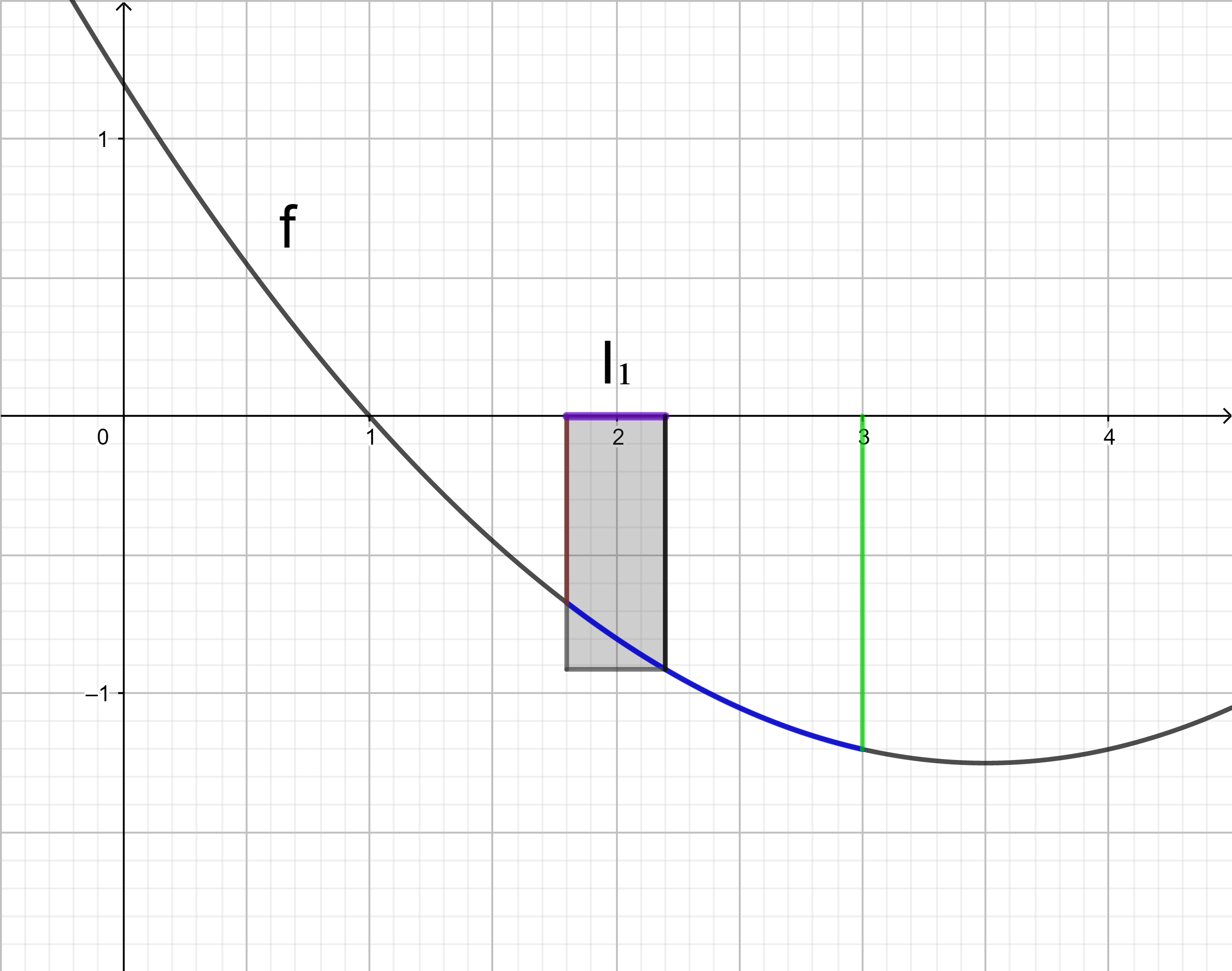
Im Intervall I1 liegt der kleinste Funktionswert an der Stelle 2,2.
(f(2,2) ist kleiner als f(1,8), da beide Funktionswerte negativ sind. Die Zahl mit dem größeren Betrag ist dann die kleinere von beiden.)
(f(2,2) ist kleiner als f(1,8), da beide Funktionswerte negativ sind. Die Zahl mit dem größeren Betrag ist dann die kleinere von beiden.)
Das Rechteck im Intervall I1 hat den orientierten Flächeninhalt 0,4 ⋅ f(2,2). Er ist negativ, da f(2,2) negativ ist.
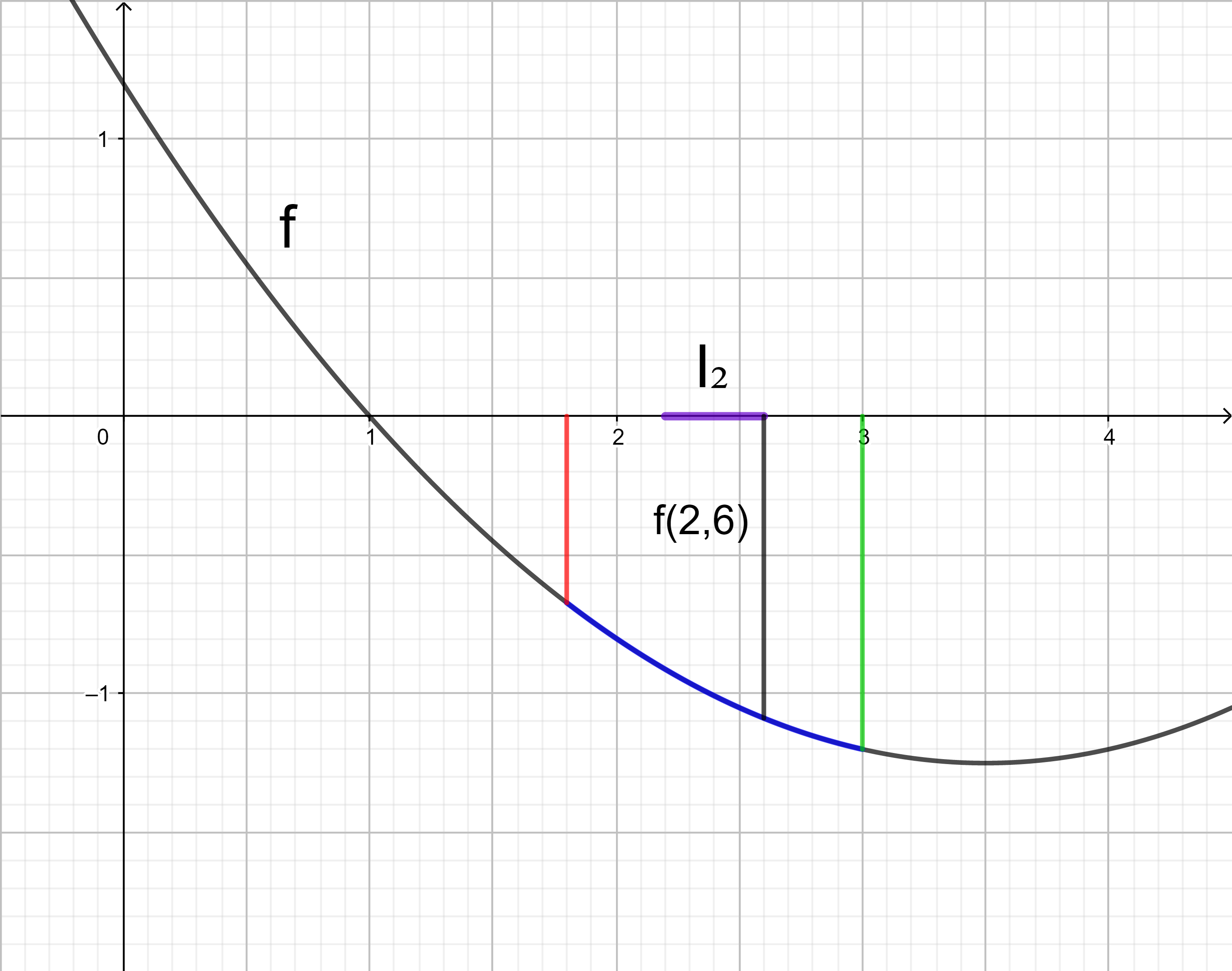
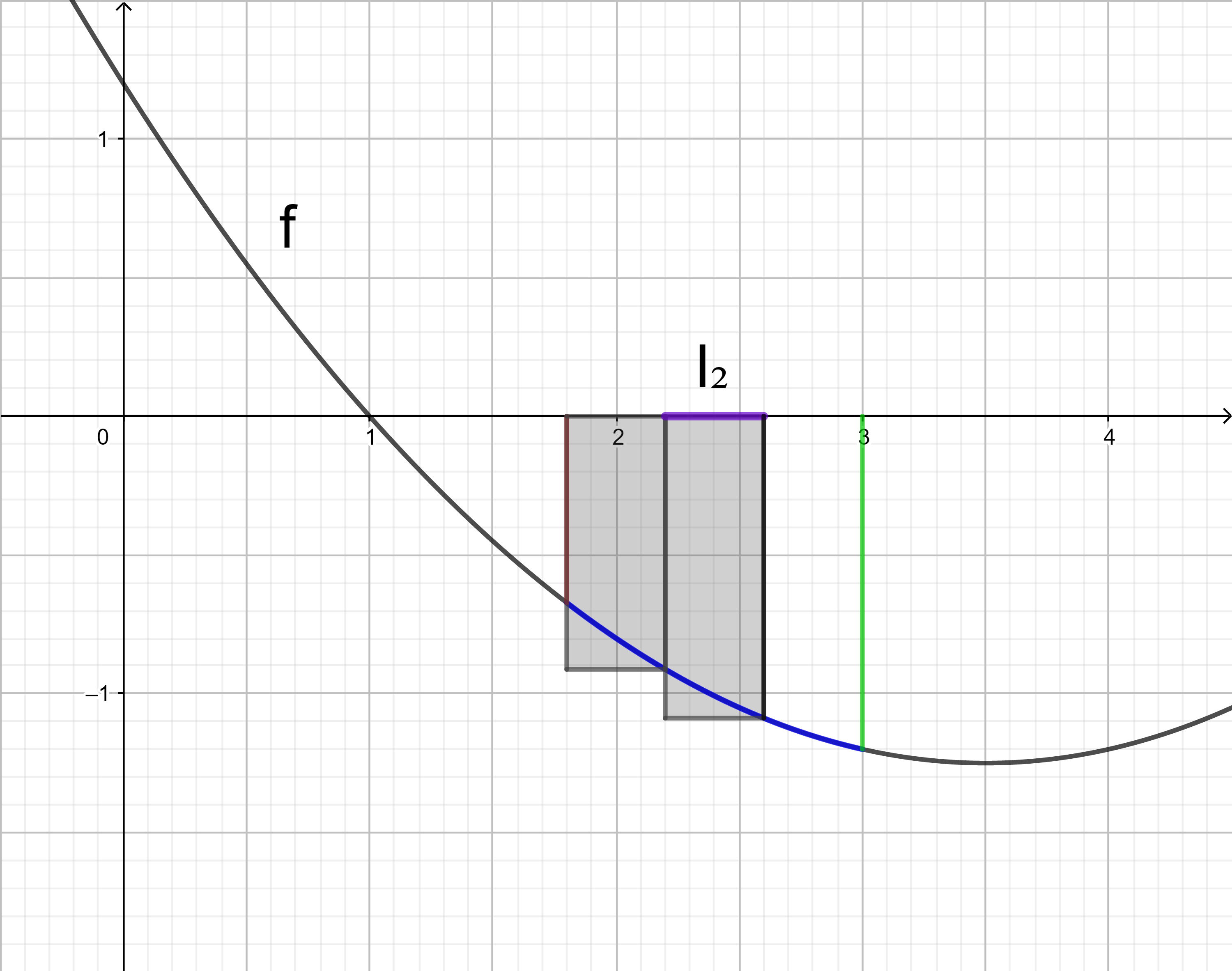
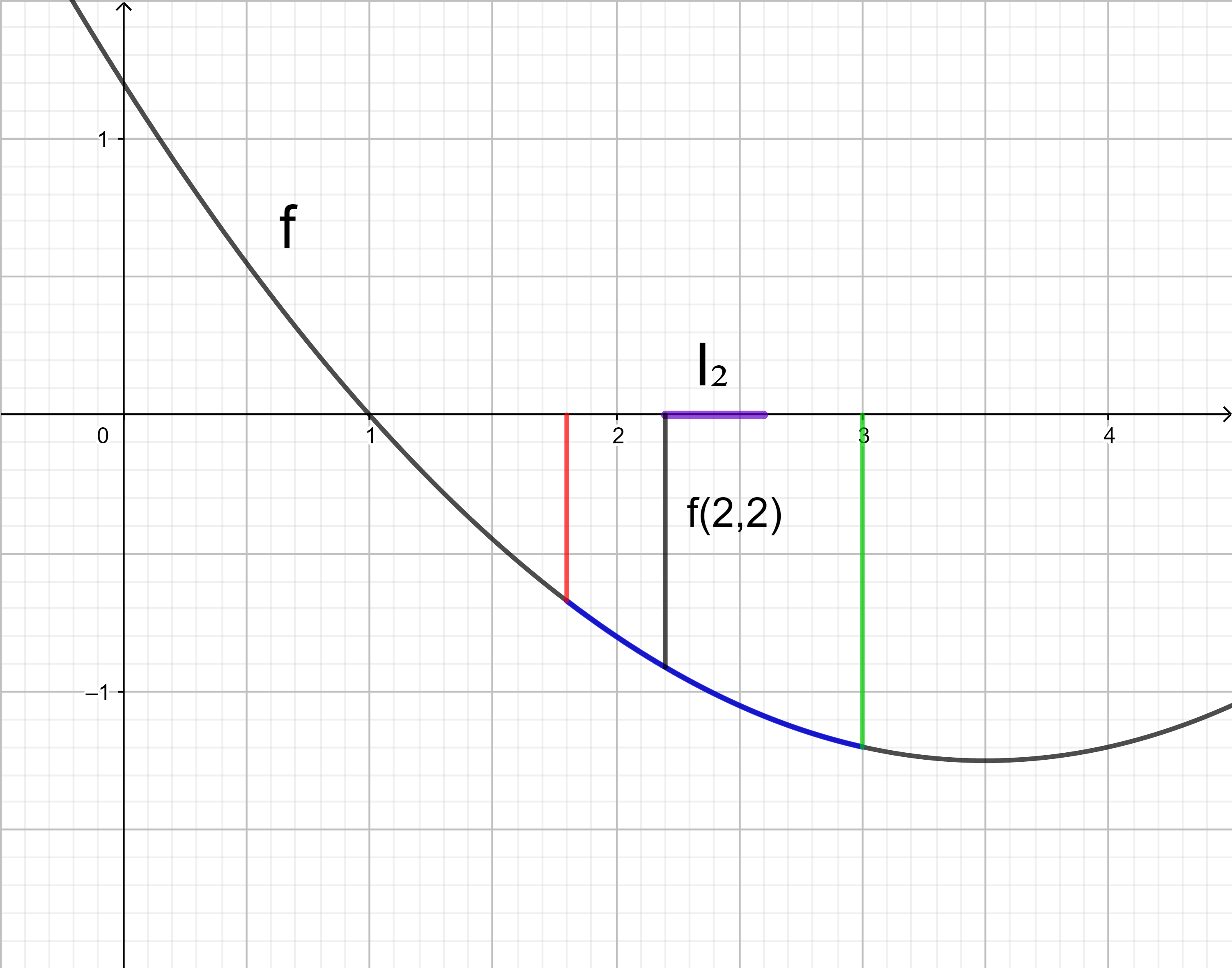
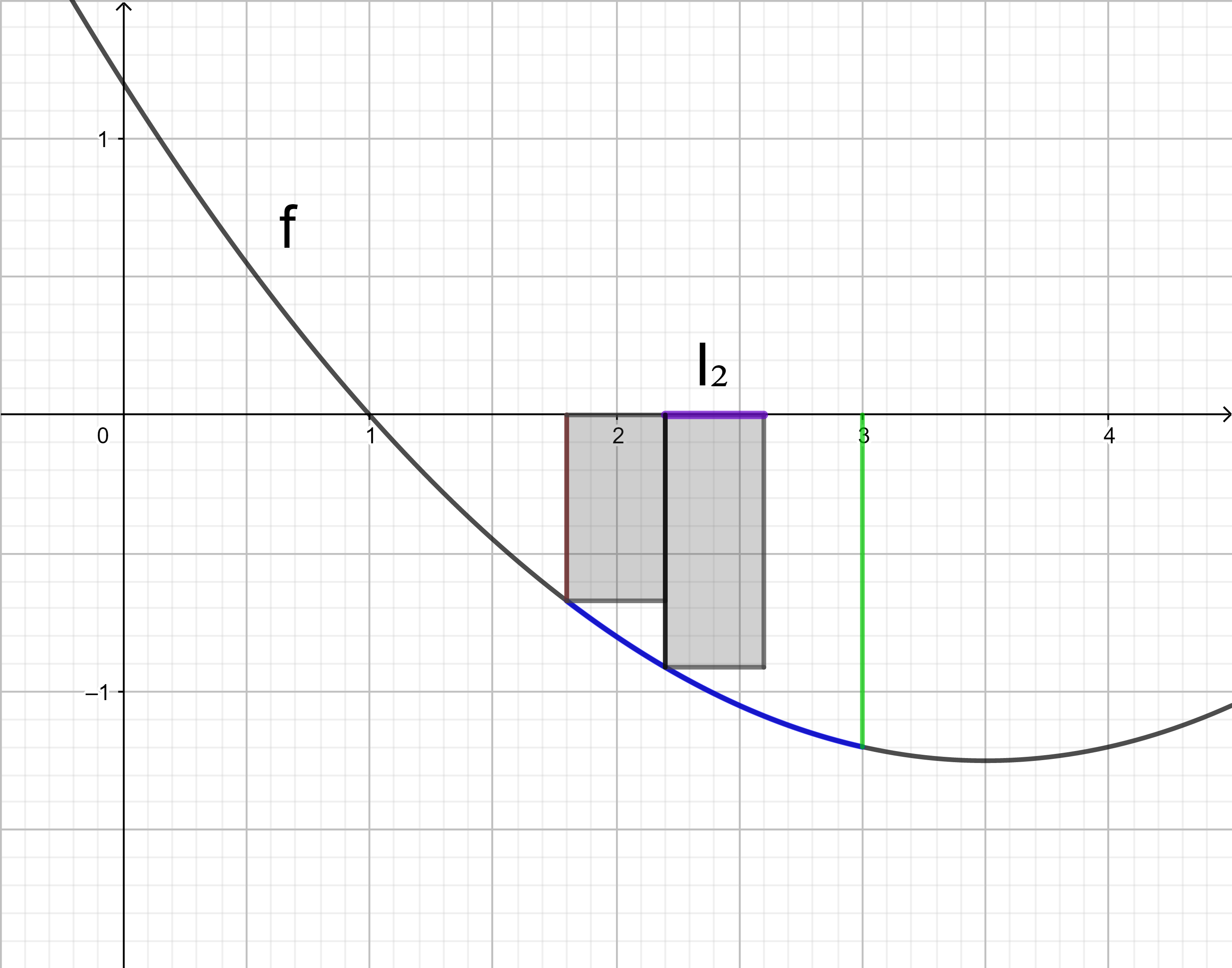
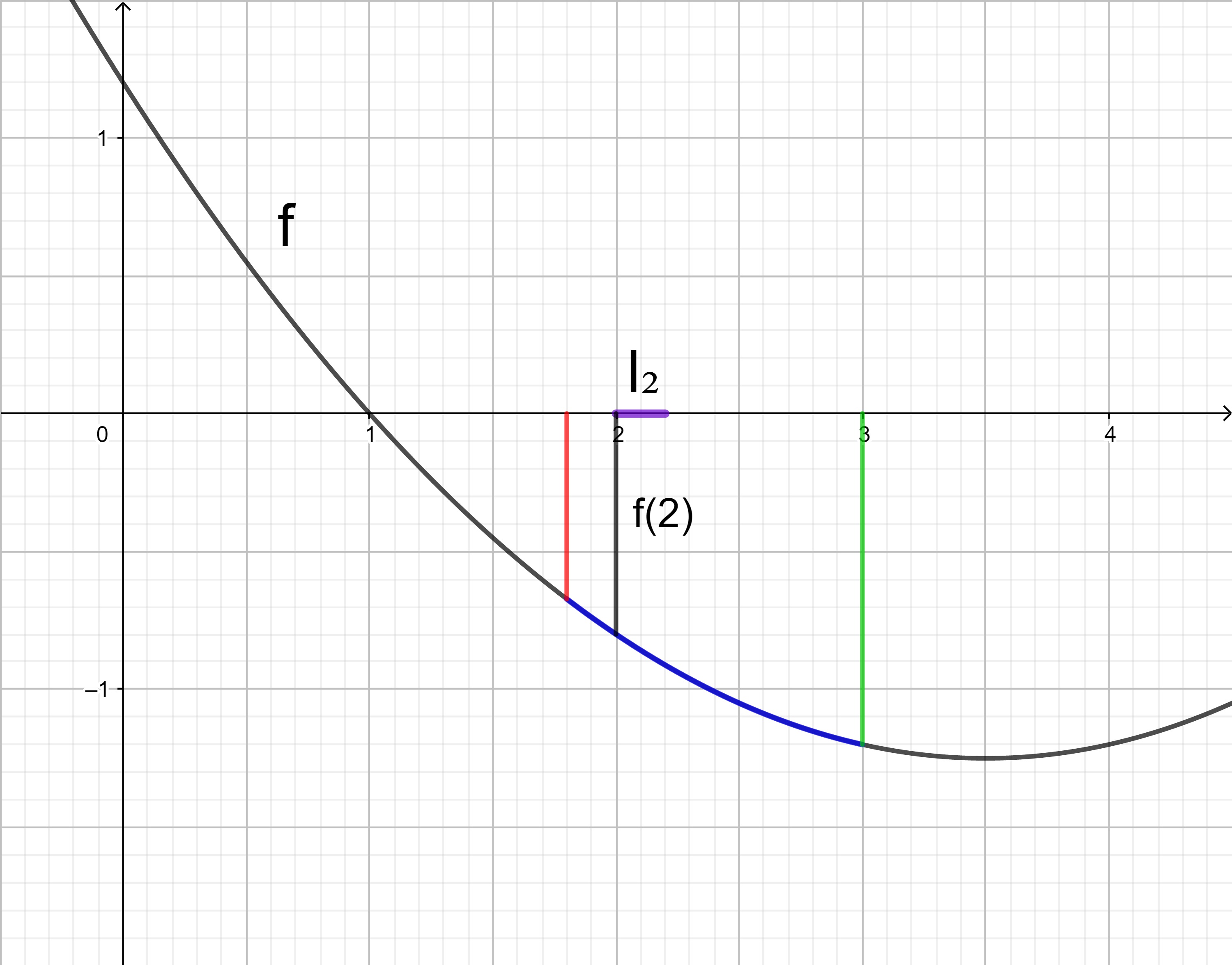
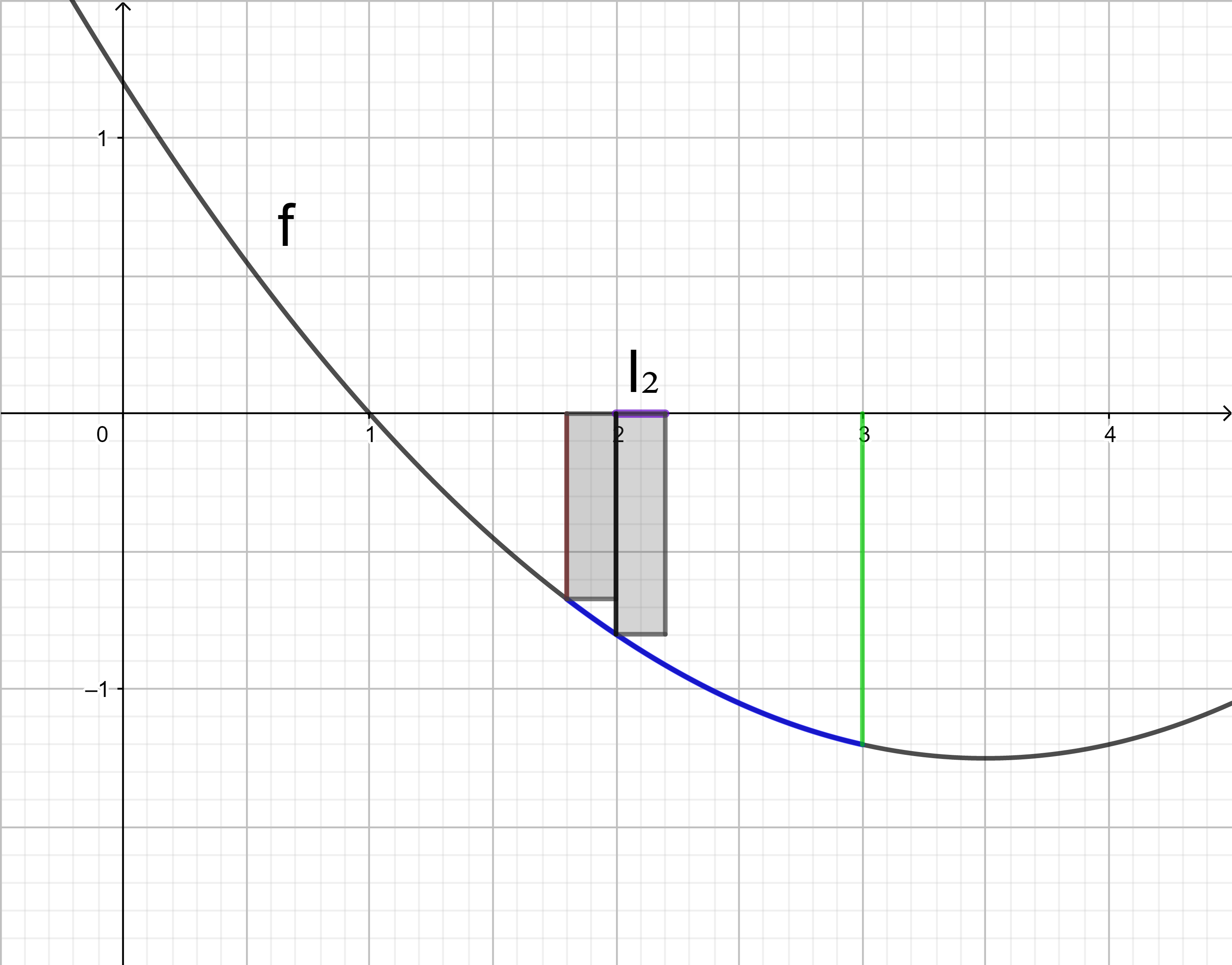
Im Intervall I2 liegt der kleinste Funktionswert an der Stelle 2,6.
Das Rechteck im Intervall I2 hat den orientierten Flächeninhalt 0,4 ⋅ f(2,6).
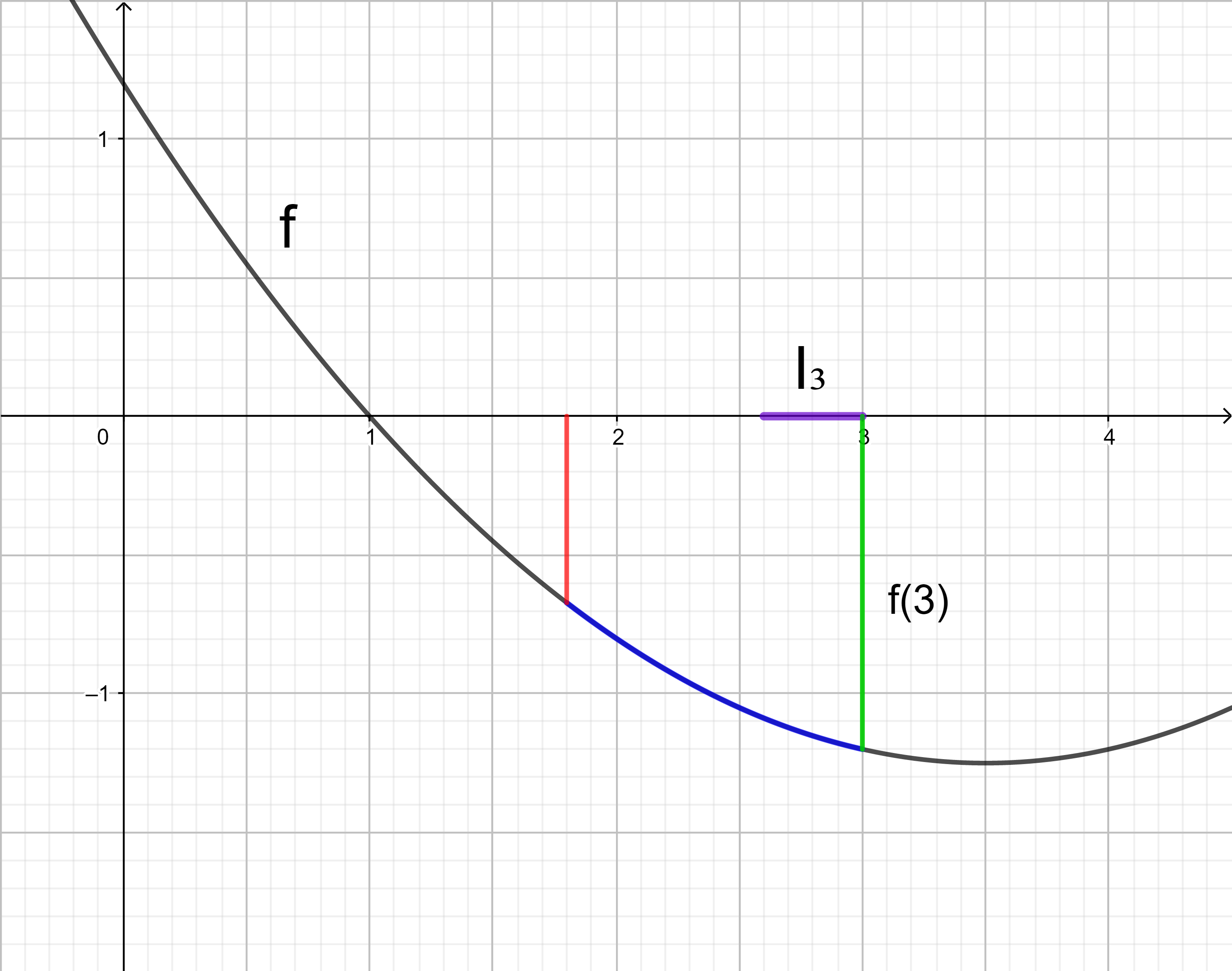
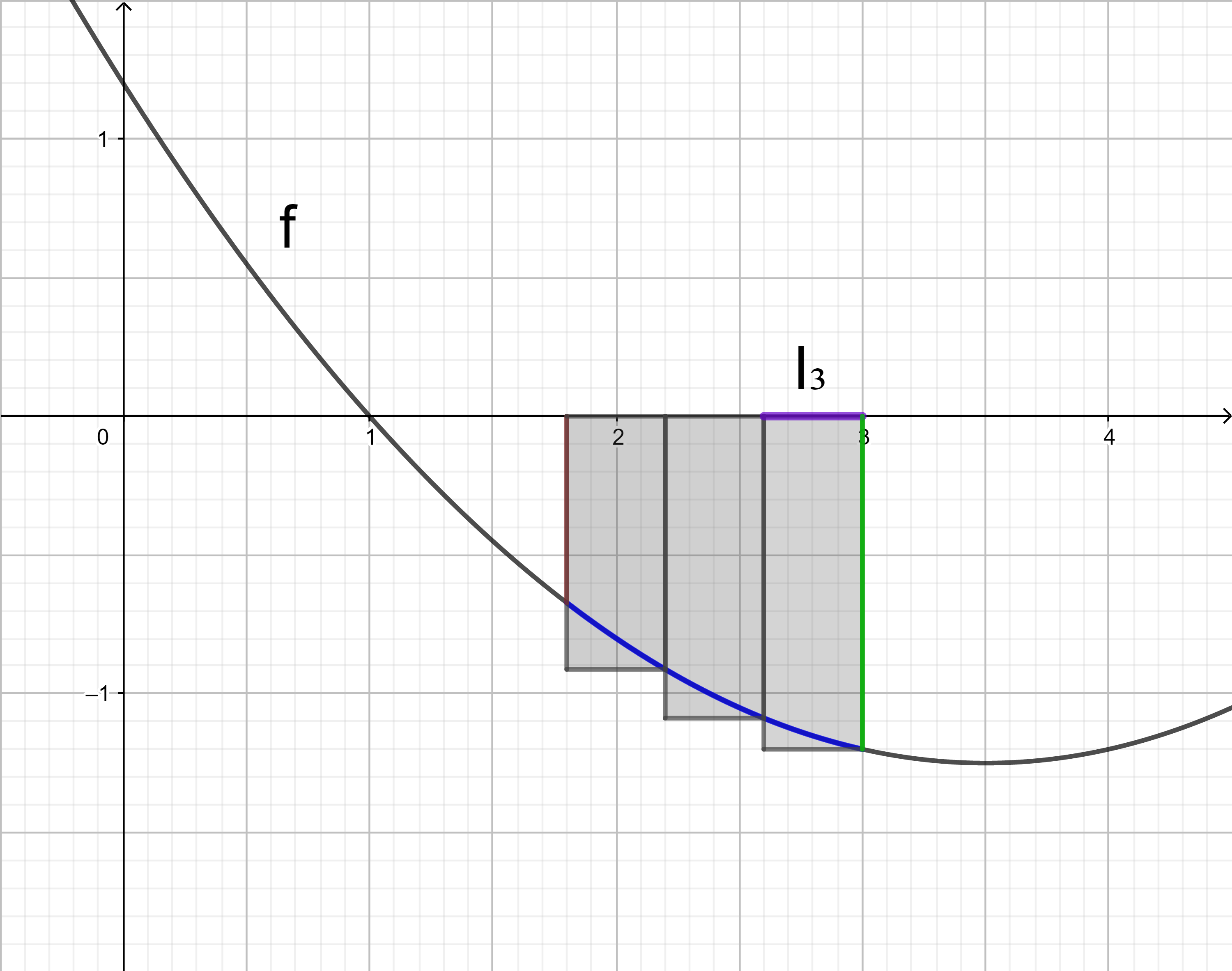
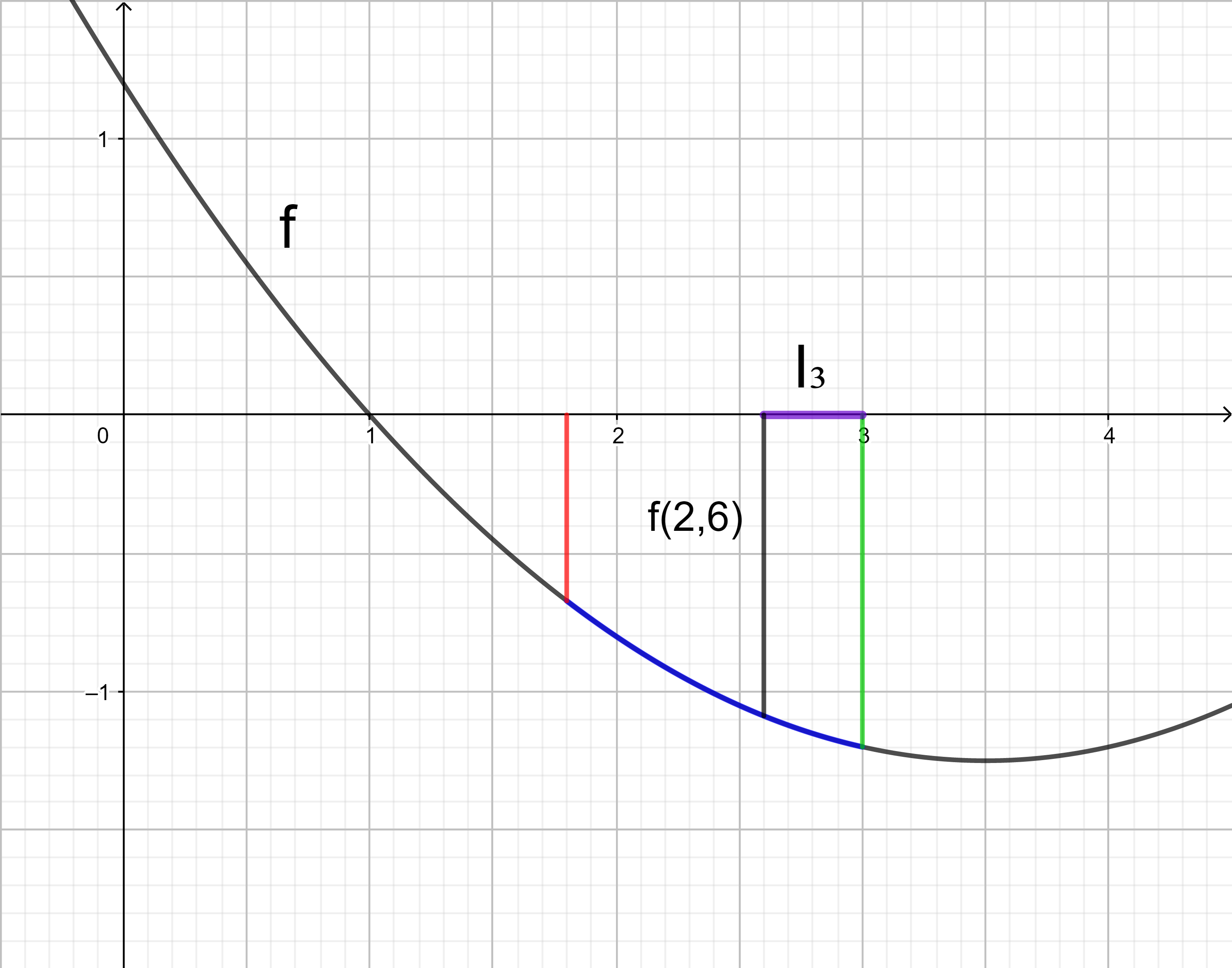
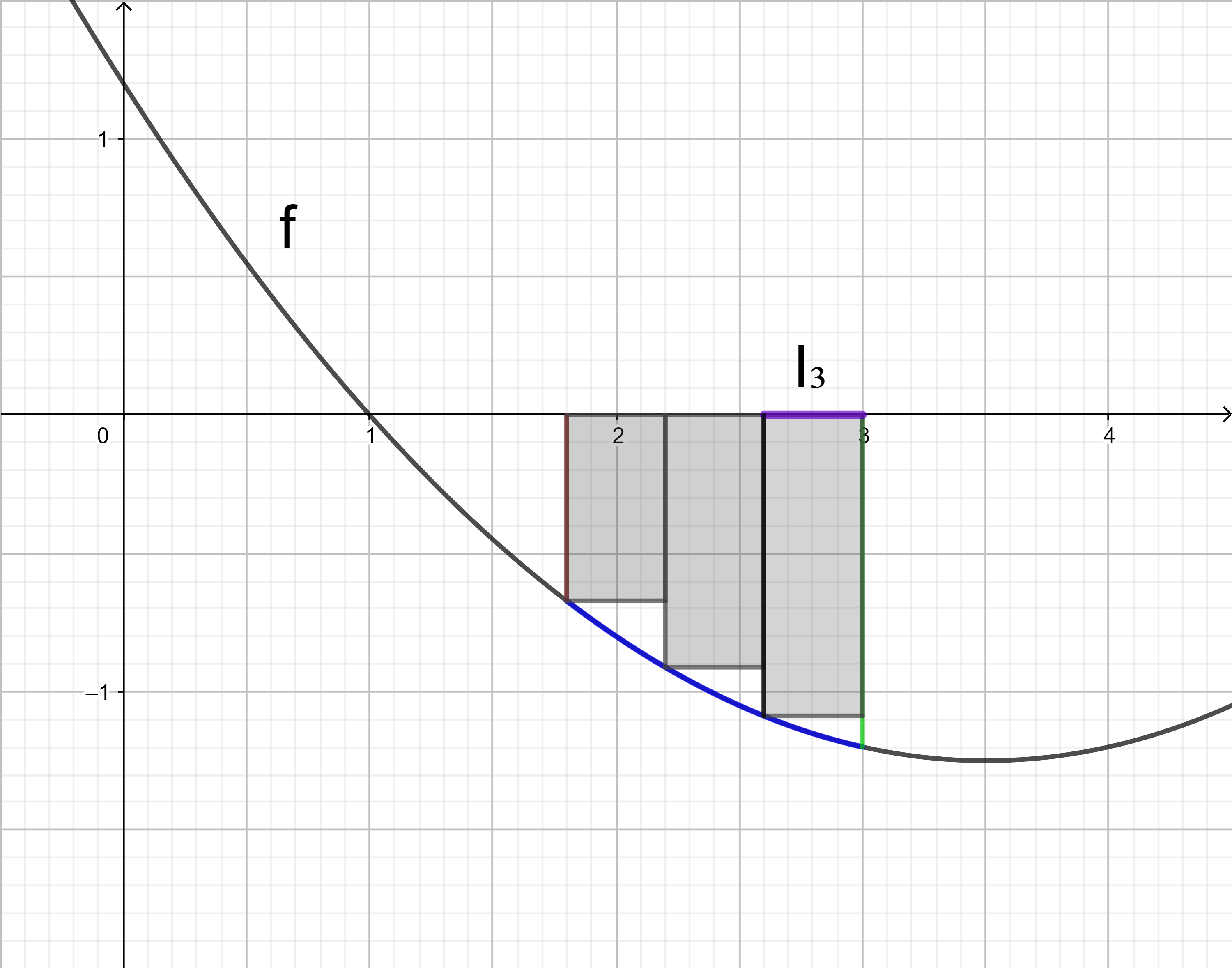
Im Intervall I3 liegt der kleinste Funktionswert an der Stelle 3.
Das Rechteck im Intervall I3 hat den orientierten Flächeninhalt 0,4 ⋅ f(3).
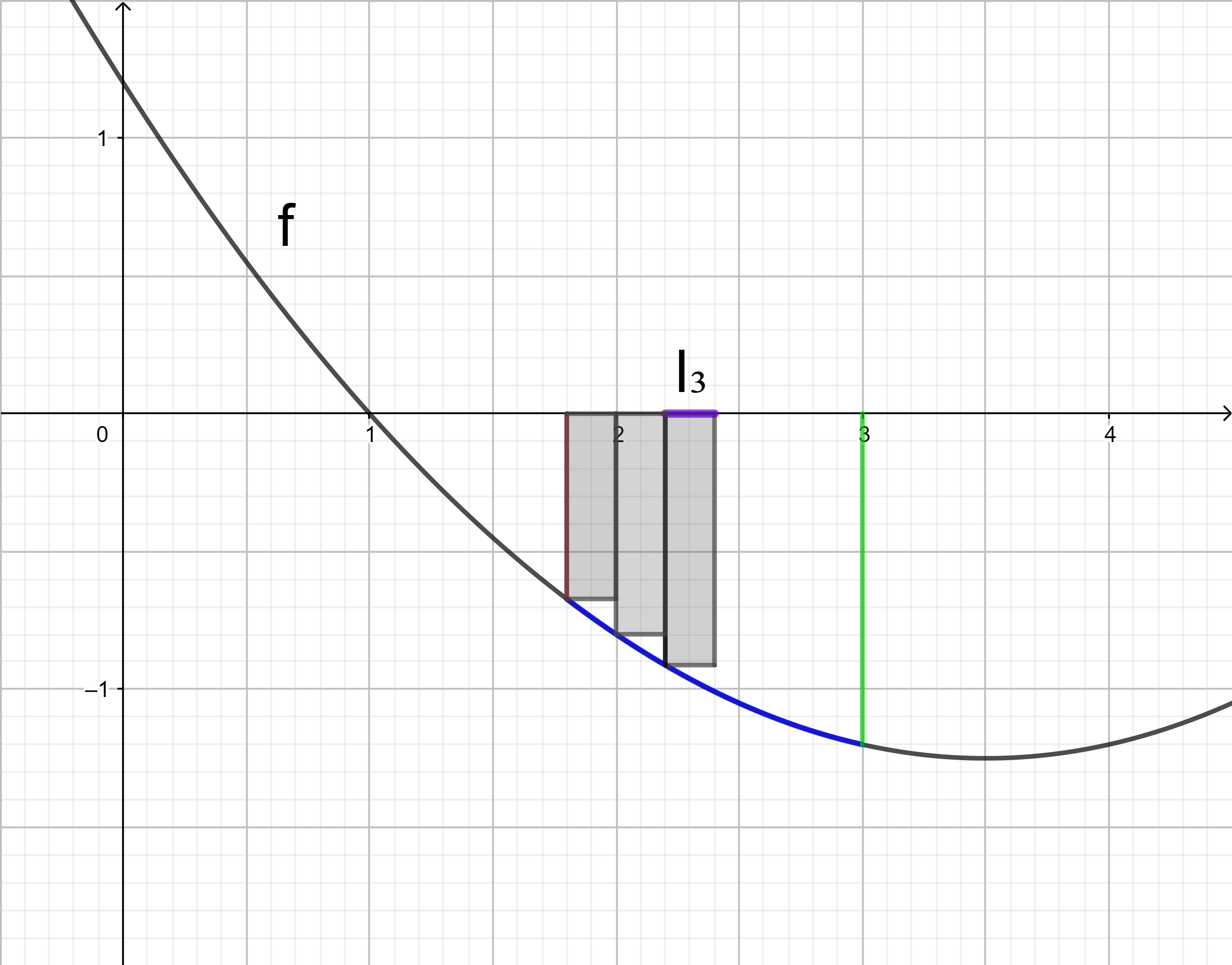
Addiert man die orientierten Flächeninhalte der drei Rechtecke, erhält man die Untersumme U3:
U3
= 0,4 ⋅ f(2,2) + 0,4 ⋅ f(2,6) + 0,4 ⋅ f(3)
= 0,4 ⋅ (f(2,2) + f(2,6) + f(3))
= 0,4 ⋅ (-0,912 + (-1,088) + (-1,2))
= 0,4 ⋅ (-3,2)
= -1,28
= 0,4 ⋅ (f(2,2) + f(2,6) + f(3))
= 0,4 ⋅ (-0,912 + (-1,088) + (-1,2))
= 0,4 ⋅ (-3,2)
= -1,28
Eine bessere Annäherung an den gesuchten Integralwert erhält man, wenn man die Untersumme U6 berechnet.
Jedes der sechs Rechtecke hat die Breite (3 - 1,8) : 6 = 1,2 : 6 = 0,2.
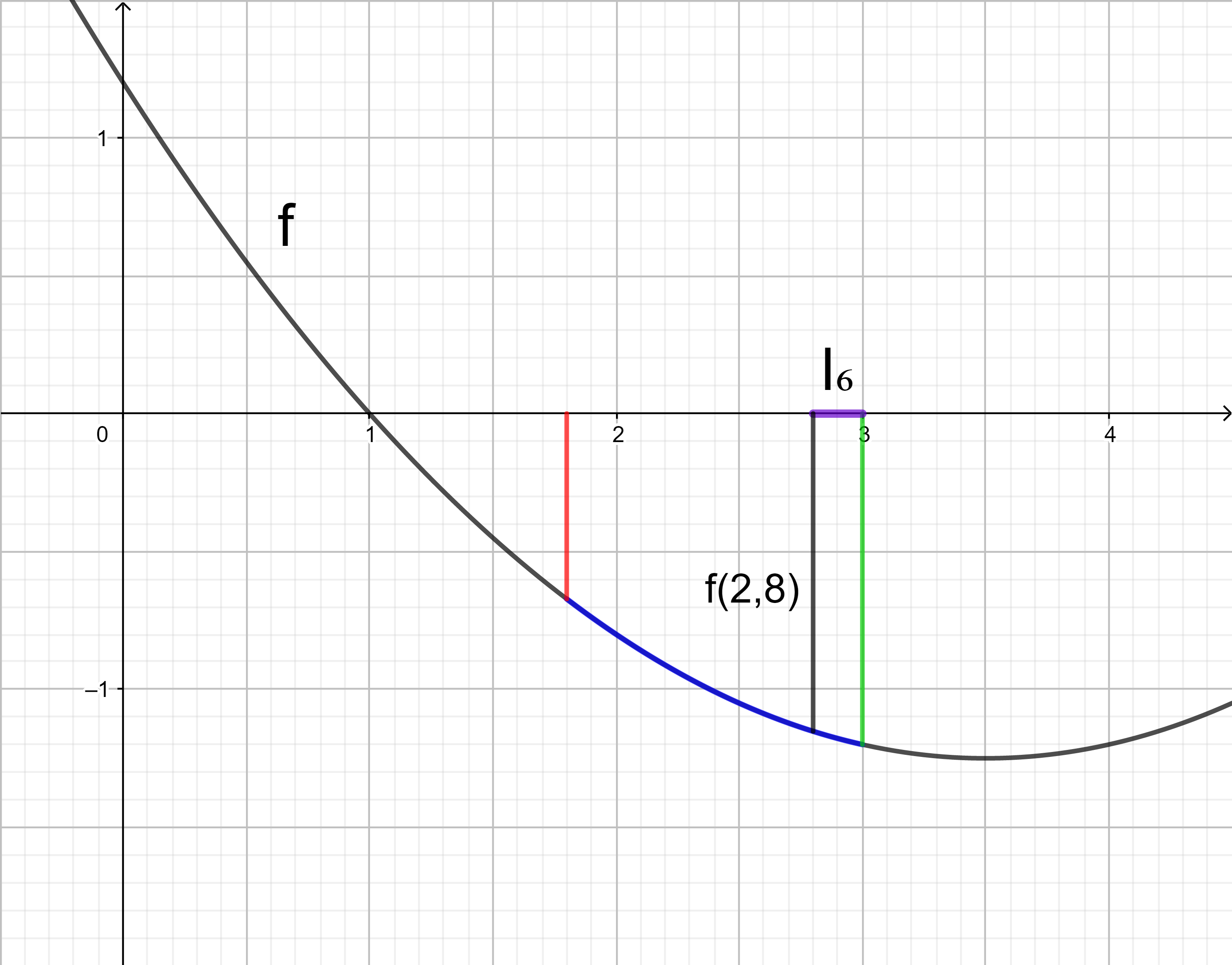
In jedem der sechs Teilintervalle wird wieder der Betrag des kleinsten Funktionswerts als Länge des jeweiligen Rechtecks festgelegt.
Jedes der sechs Rechtecke hat die Breite (3 - 1,8) : 6 = 1,2 : 6 = 0,2.
In jedem der sechs Teilintervalle wird wieder der Betrag des kleinsten Funktionswerts als Länge des jeweiligen Rechtecks festgelegt.
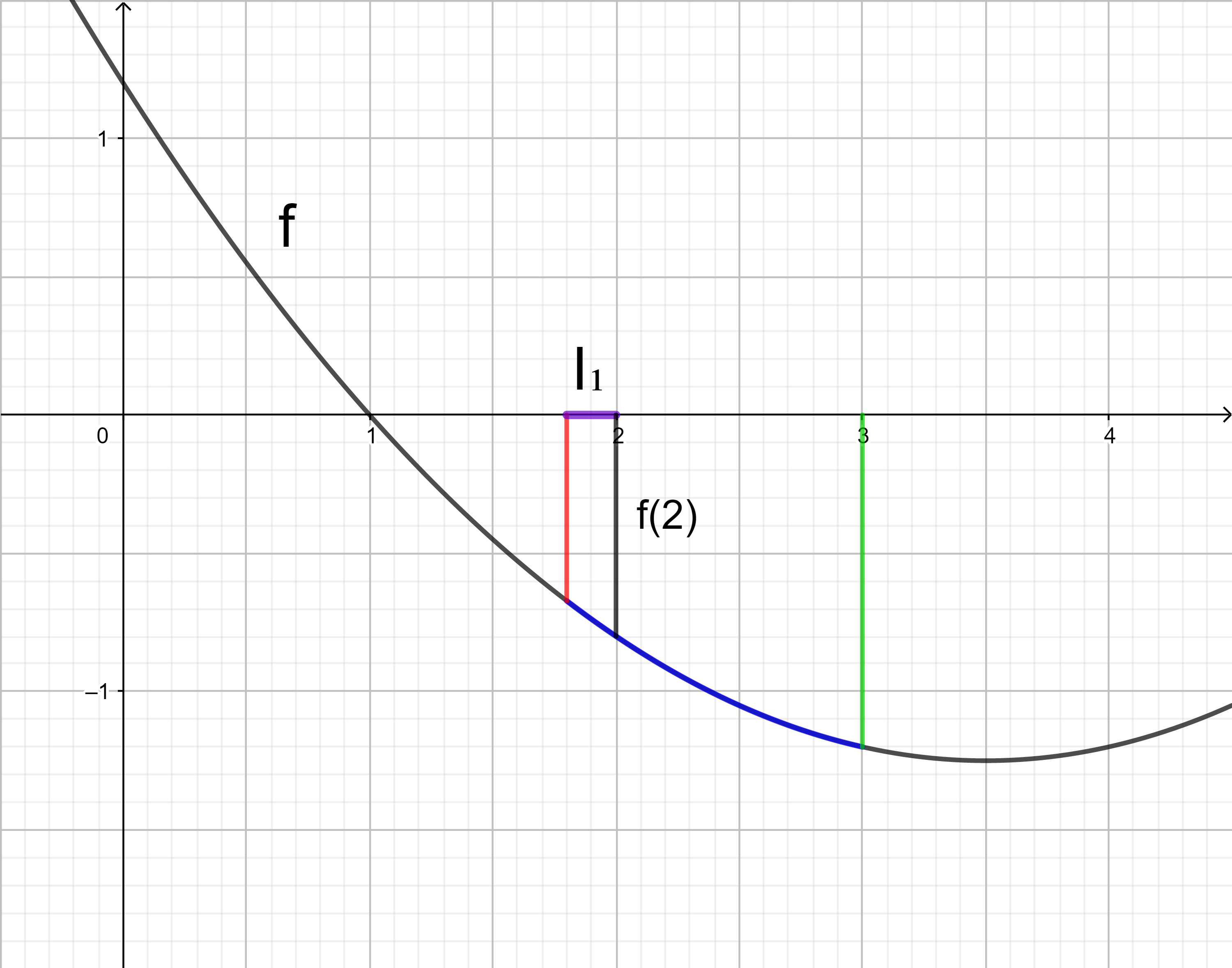
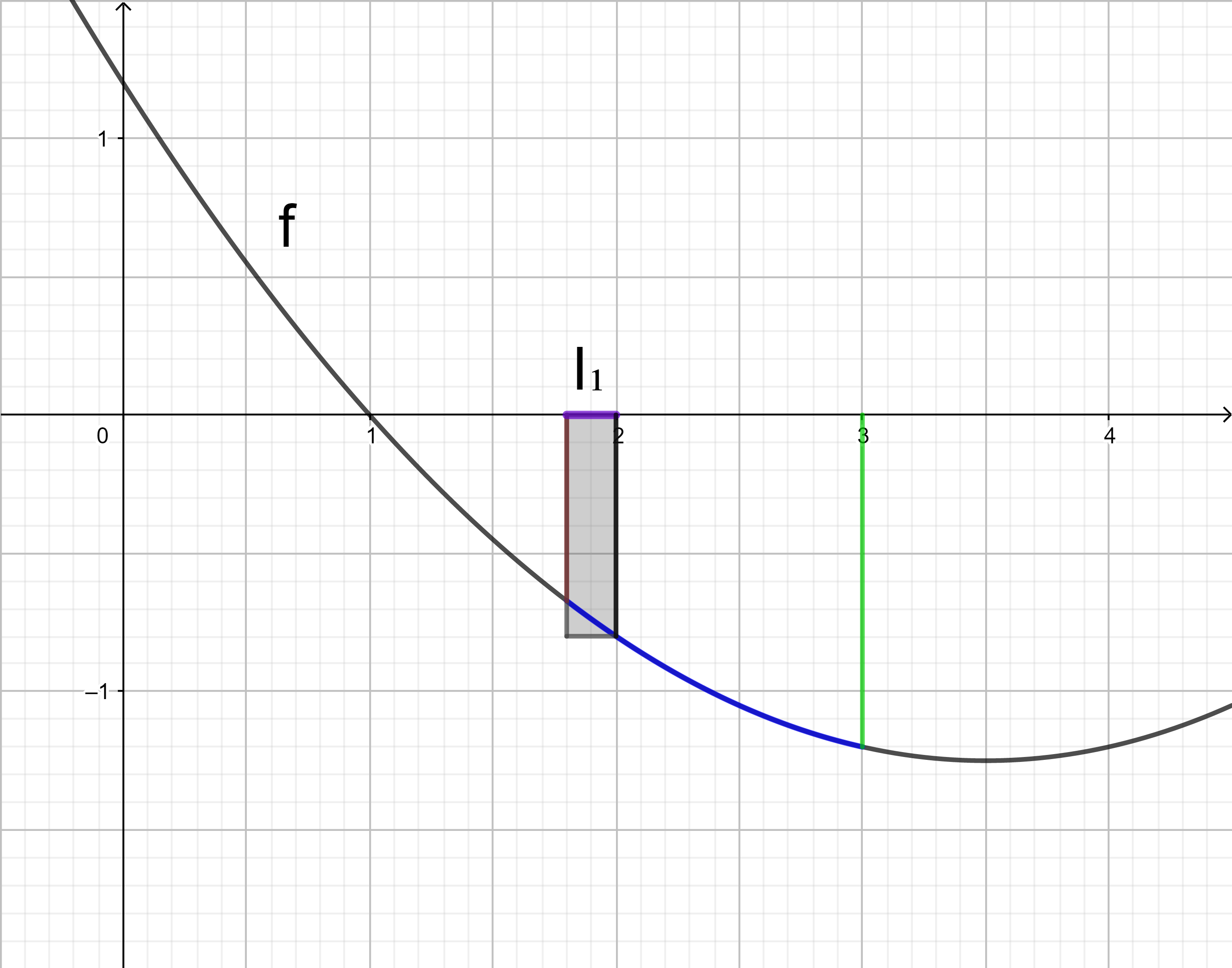
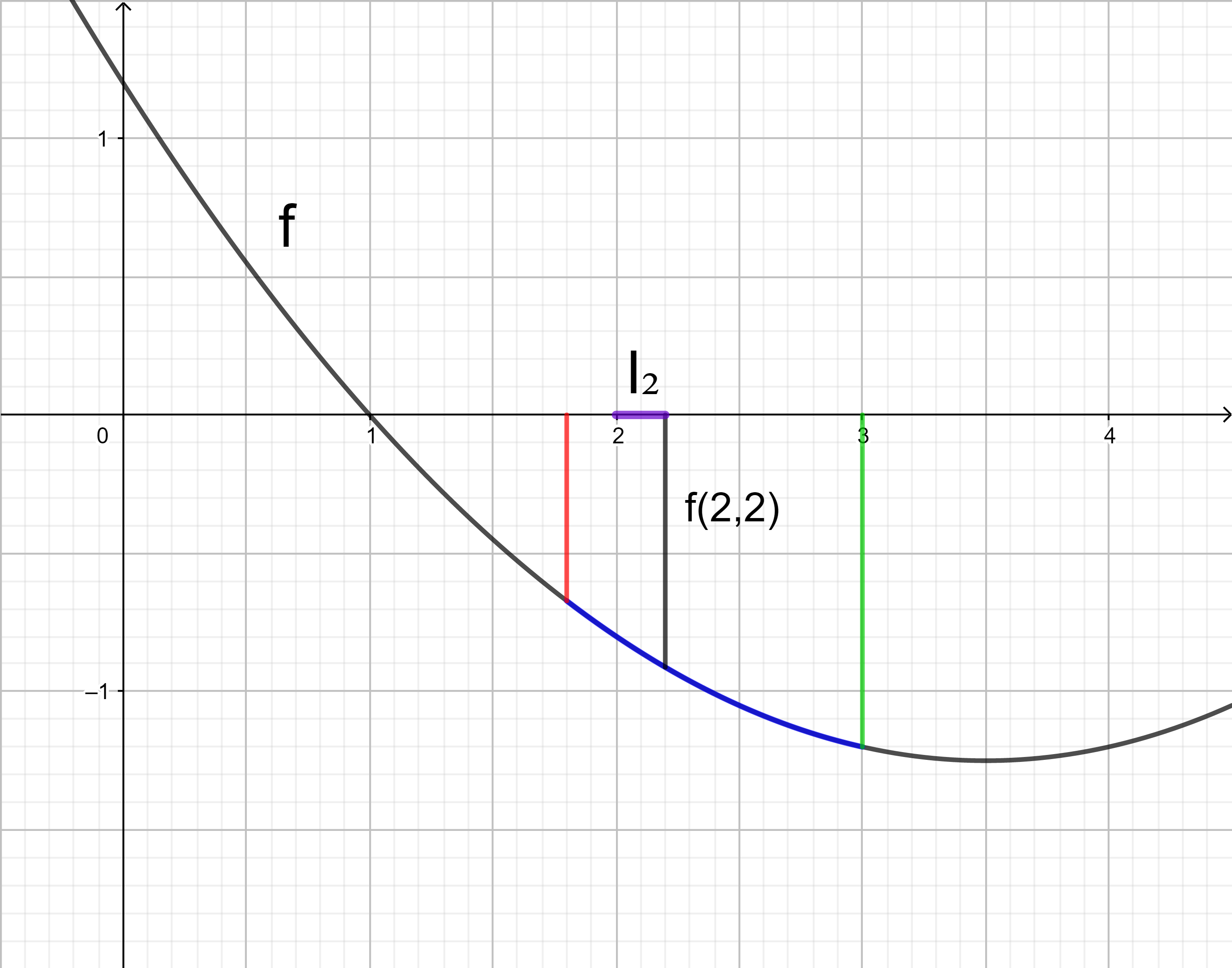
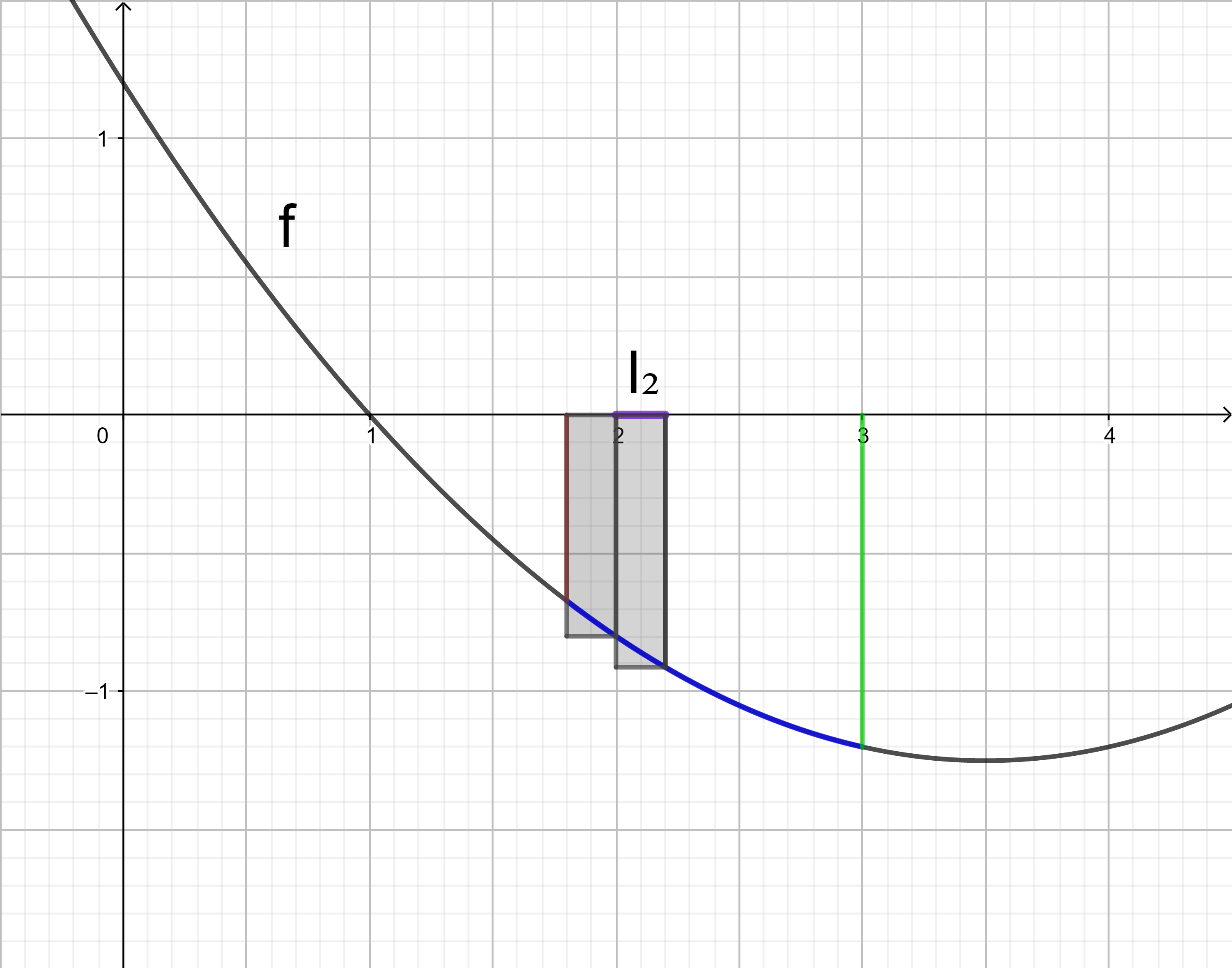
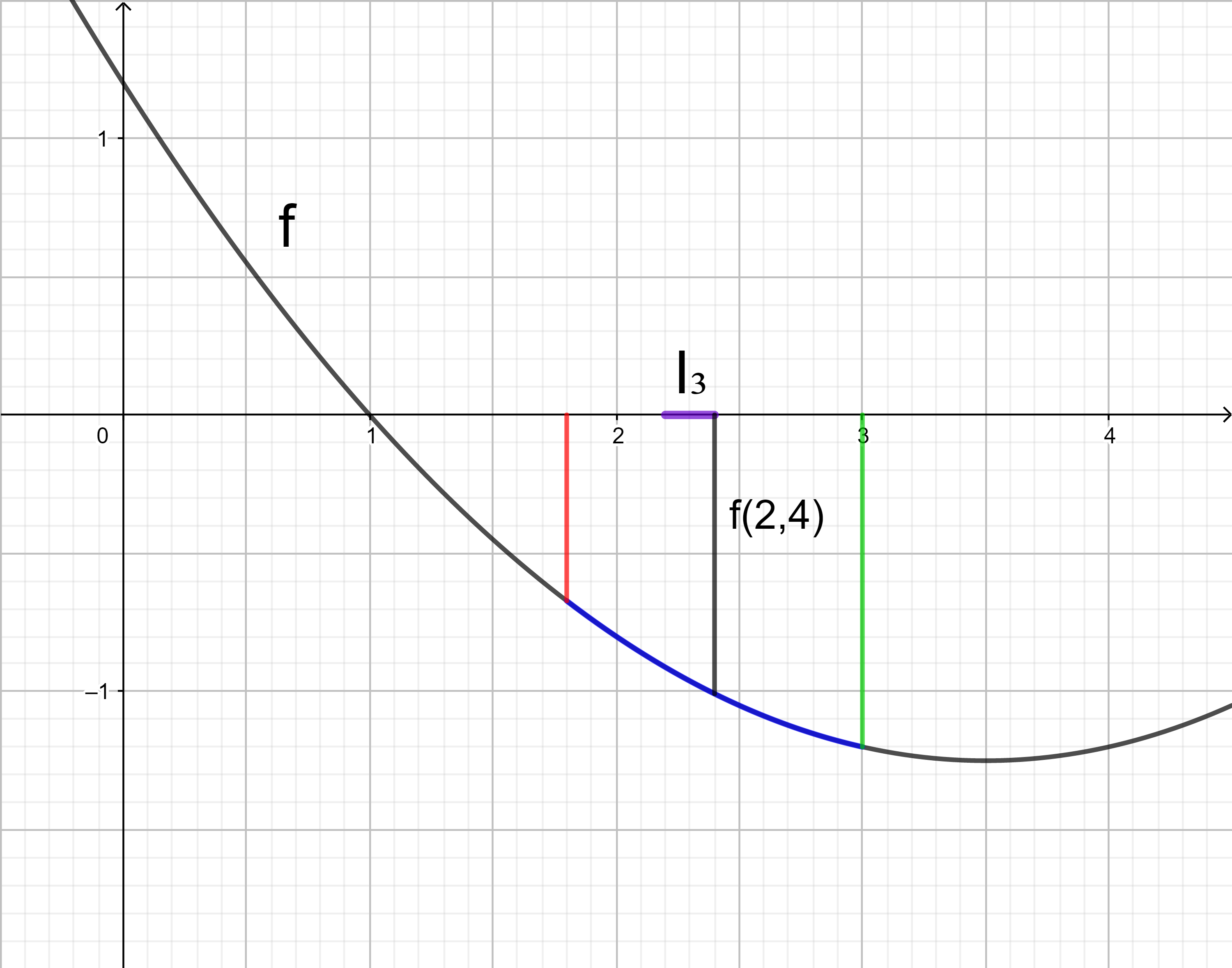
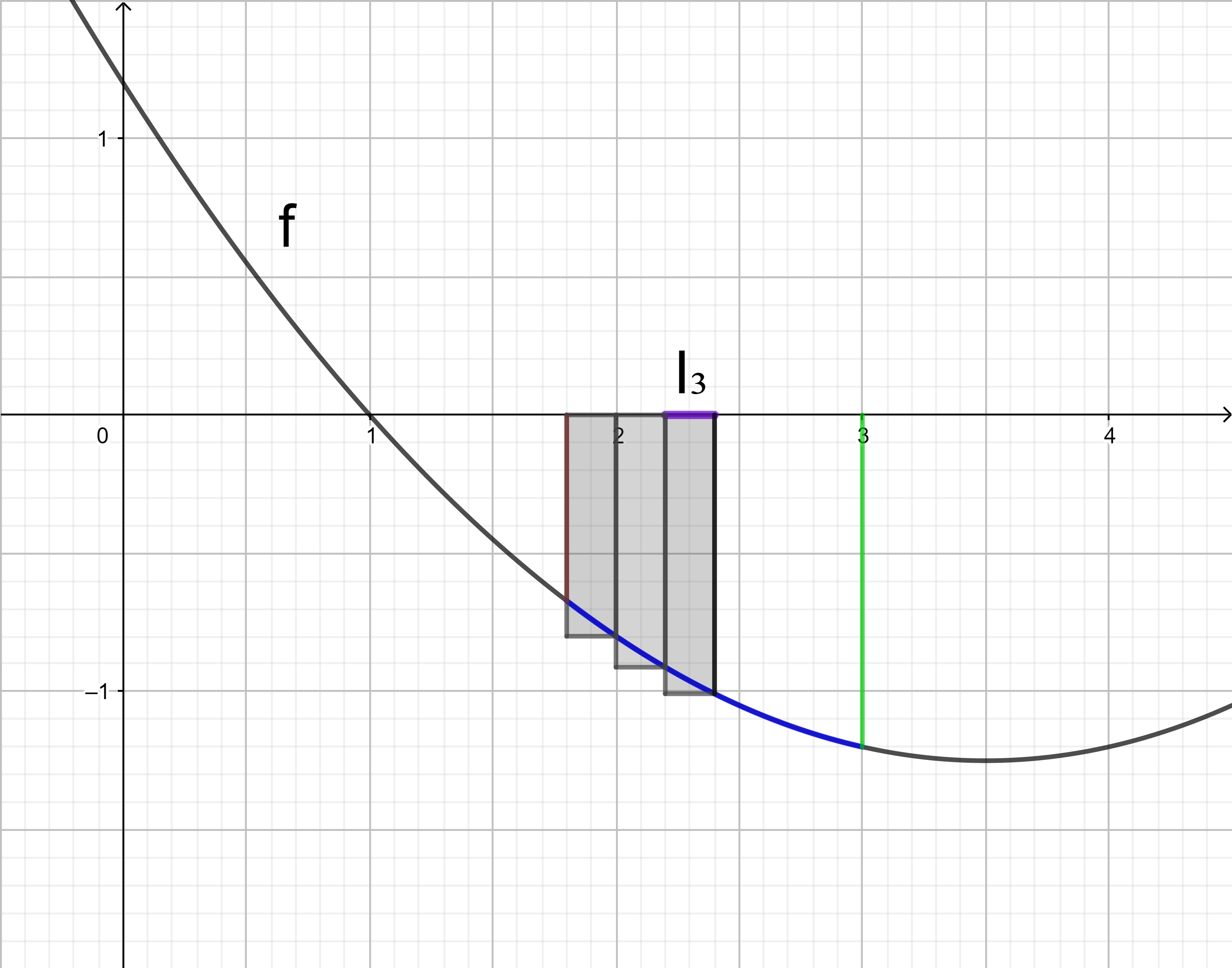
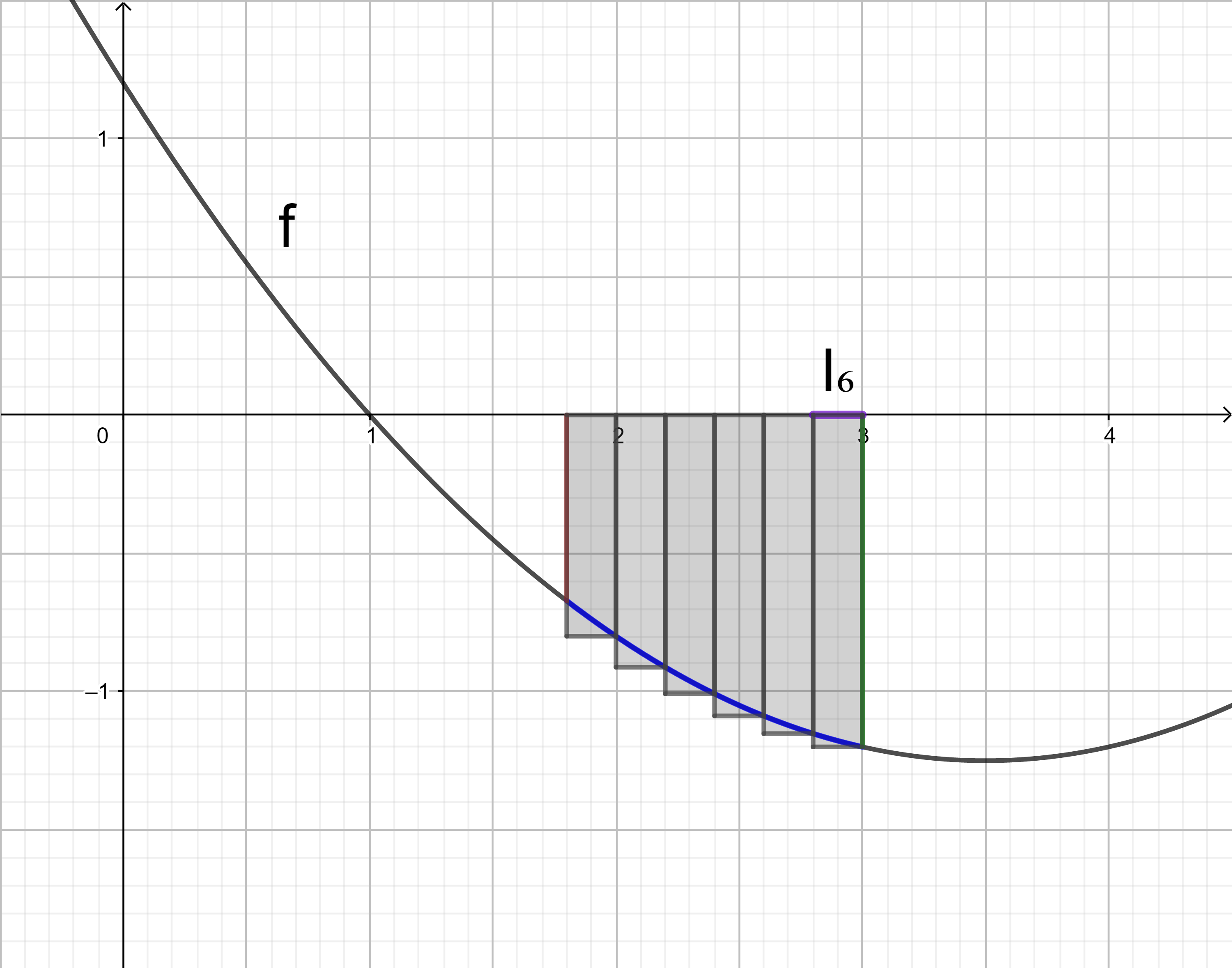
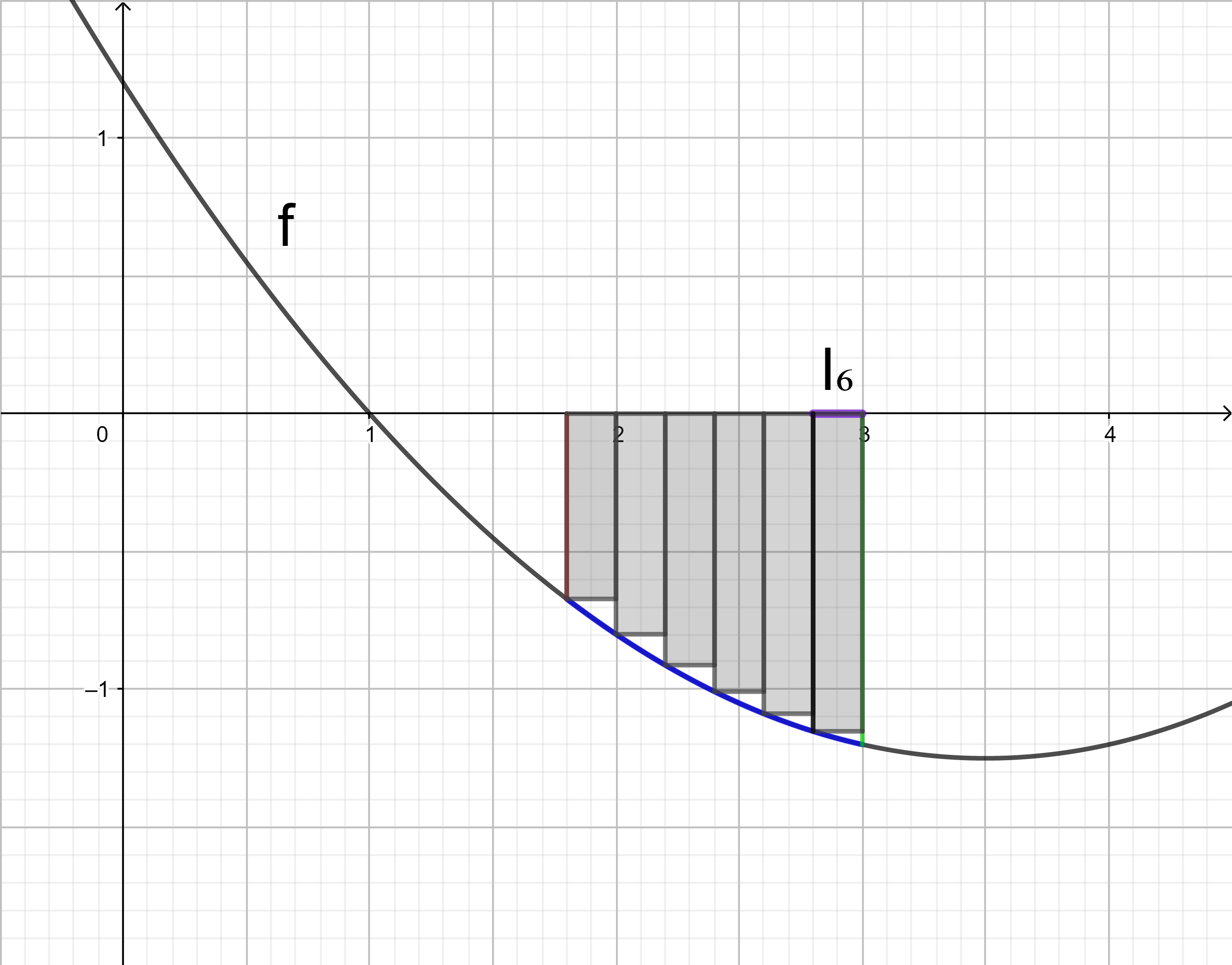
Die Untersumme U6 wird entsprechend der Untersumme U3 berechnet:
U6
= 0,2 ⋅ f(2) + 0,2 ⋅ f(2,2) + 0,2 ⋅ f(2,4) + 0,2 ⋅ f(2,6) + 0,2 ⋅ f(2,8) + 0,2 ⋅ f(3)
= 0,2 ⋅ (f(2) + f(2,2) + f(2,4) + f(2,6) + f(2,8) + f(3))
= 0,2 ⋅ (-0,8 + (-0,912) + (-1,008) + (-1,088) + (-1,152) + (-1,2))
= 0,2 ⋅ (-6,16)
= -1,232
= 0,2 ⋅ (f(2) + f(2,2) + f(2,4) + f(2,6) + f(2,8) + f(3))
= 0,2 ⋅ (-0,8 + (-0,912) + (-1,008) + (-1,088) + (-1,152) + (-1,2))
= 0,2 ⋅ (-6,16)
= -1,232
Wie im Beispiel 1 kann auch hier der gesuchte Integralwert mit Hilfe von Obersummen angenähert werden. Zur Obersumme O3 gehören wie bei der Untersumme U3 drei Rechtecke mit der Breite 0,4. Das Intervall [1,8 ; 3] wird wieder in drei Teilintervalle I1, I2 und I3 unterteilt. Da die Obersumme O3 größer als der gesuchte Integralwert sein soll, wird in jedem Teilintervall der größte Funktionswert gesucht und dessen Betrag als Länge des jeweiligen Rechtecks festgelegt.
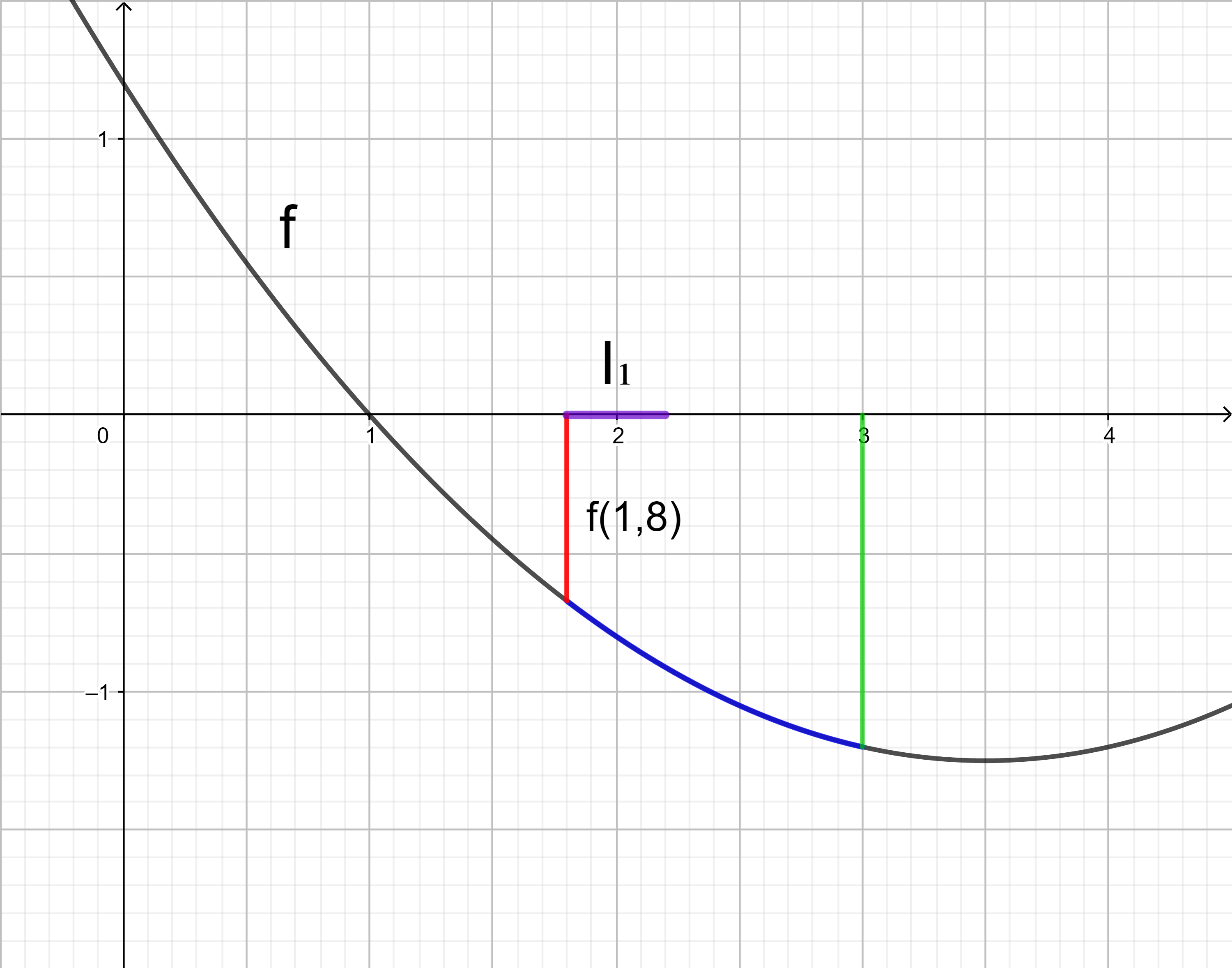
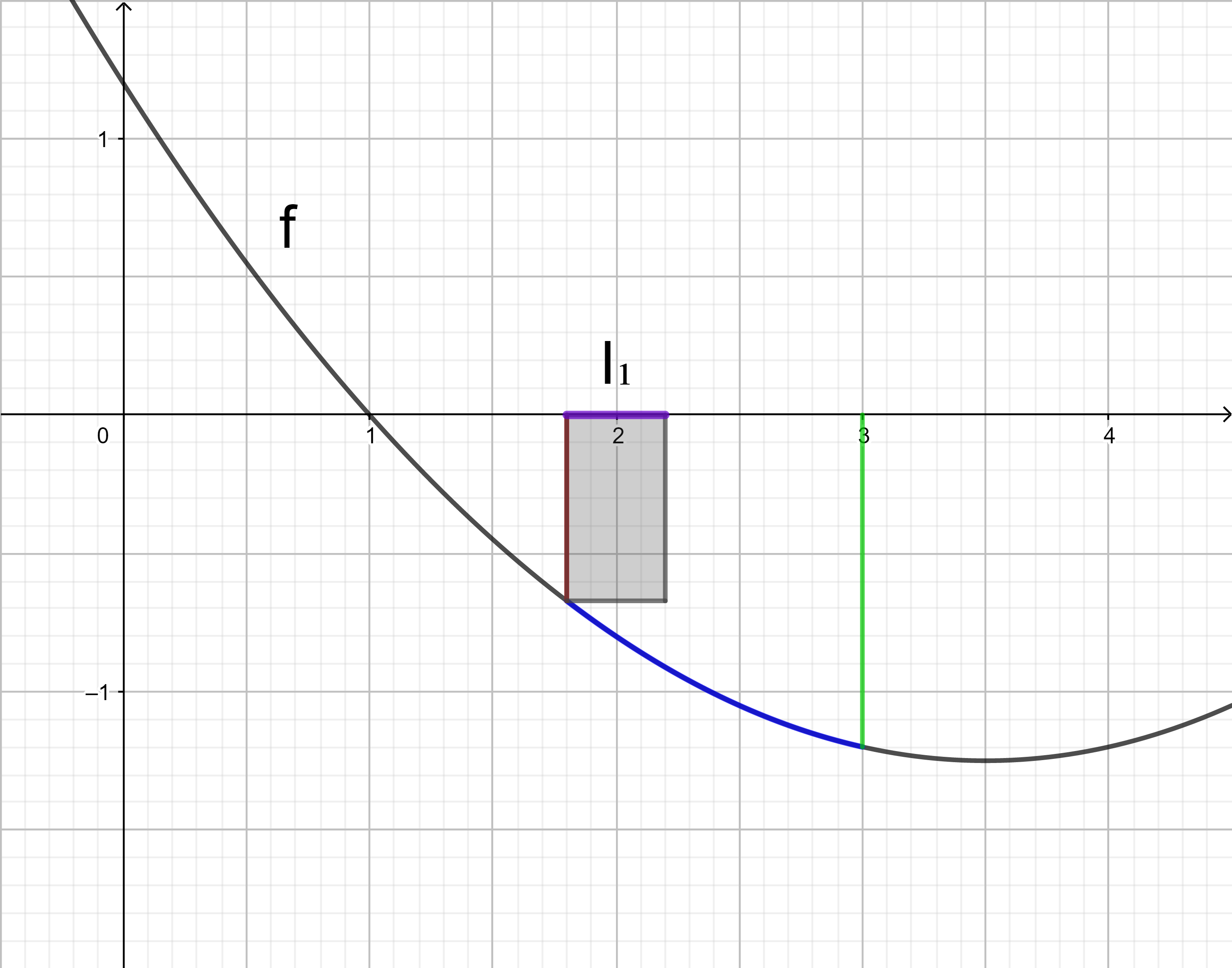
Die Obersumme O3 wird entsprechend der Untersumme U3 berechnet:
O3
= 0,4 ⋅ f(1,8) + 0,4 ⋅ f(2,2) + 0,4 ⋅ f(2,6)
= 0,4 ⋅ (f(1,8) + f(2,2) + f(2,6))
= 0,4 ⋅ (-0,672 + (-0,912) + (-1,088))
= 0,4 ⋅ (-2,672)
= -1,0688
= 0,4 ⋅ (f(1,8) + f(2,2) + f(2,6))
= 0,4 ⋅ (-0,672 + (-0,912) + (-1,088))
= 0,4 ⋅ (-2,672)
= -1,0688
Die Konstruktion der Rechtecke zur Obersumme O6 entspricht der Konstruktion der Rechtecke zur Obersumme O3 (Betrag des größten Funktionswertes als Länge des Rechtecks) und zur Untersumme U6 (0,2 als Breite des Rechtecks).
O6
= 0,2 ⋅ f(1,8) + 0,2 ⋅ f(2) + 0,2 ⋅ f(2,2) + 0,2 ⋅ f(2,4) + 0,2 ⋅ f(2,6) + 0,2 ⋅ f(2,8)
= 0,2 ⋅ (f(1,8) + f(2) + f(2,2) + f(2,4) + f(2,6) + f(2,8))
= 0,2 ⋅ (-0,672 + (-0,8) + (-0,912) + (-1,008) + (-1,088) + (-1,152))
= 0,2 ⋅ (-5,632)
= -1,1264
= 0,2 ⋅ (f(1,8) + f(2) + f(2,2) + f(2,4) + f(2,6) + f(2,8))
= 0,2 ⋅ (-0,672 + (-0,8) + (-0,912) + (-1,008) + (-1,088) + (-1,152))
= 0,2 ⋅ (-5,632)
= -1,1264
Der Wert des Integrals
3
∫
f(x)
dx
1,8
ist also größer als U6 = -1,232 und kleiner als O6 = -1,1264.
Er beträgt genau -1,1808.
(Wie man den Wert eines Integrals exakt berechnet, erfahren Sie in den nachfolgenden Kapiteln.)